ЗАДАЧИ МАТЕМАТИЧЕСКОГО ПРОГРАММИРОВАНИЯ

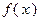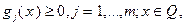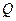Математическое программирование – раздел прикладной математики, занимающийся изучением задач отыскания экстремума функций на некотором множестве и разработкой методов решения этих задач. Под общей задачей математического программирования понимают задачу отыскания точки экстремума (при этом всегда указывается конкретно: максимума или минимума) функции при условиях где – некоторое множест-

во в пространстве векторов 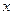. Функция 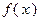называется целевой, а 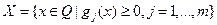– допустимым множеством. Подобные задачи часто трактуются как оптимизационные и рассматриваются в рамках теории оптимизации. Заметим, что задача на максимум легко сводится к задаче на минимум и наоборот, т.к. например точка максимума функции 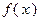совпадает с точкой минимума функции 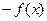. В соответствии с изложенным задача на максимум может быть поставлена в виде

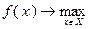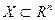, , (1.1)

где 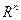– n-мерное вещественное линейное пространство. Решить задачу (1.1) означает найти (хотя бы одну) точку 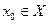, в которой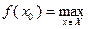 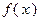. Задача отыскания всех точек 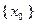не ставится, с одной стороны, из-за сложности, с другой – по причине отсутствия практической потребности. Задачу (1.1), также как и другие задачи, в которых 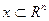, относят к классу задач конечномерной оптимизации.

Важной разновидностью задач математического программирования являются задачи линейного программирования. Задача линейного программирования может быть поставлена, например, следующим образом:

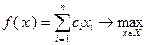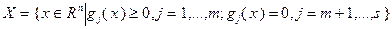, , (1.2)

где 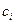– заданные числа 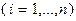, 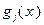– линейные функции ,

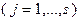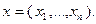Если в (1.2) хотя бы одна из функций 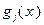нелинейна, то будем иметь задачу нелинейного программирования.

Задачи вида 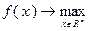относят к классу задач безусловной оптимизации. Отметим также, что вместо целевой функции может быть использован целевой функционал, который, как известно, представляет собой числовую функцию, определенную на некотором множестве функций (например, это может быть интеграл, наибольшее значение функции на некотором множестве значений аргумента и т.д.). Далее рассмотрим некоторые примеры постановок практических задач.

Задача № 1. Планирование производства

Исходные данные:

n – число видов производимых товаров;

m – число видов имеющихся ресурсов;

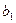– имеющееся количество единиц ресурса 1-го вида;

……………………………………………………………….

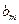– имеющееся количество единиц ресурса m-го вида;

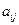– количество единиц ресурса i-го вида, требуемое для производства единицы товара j-го вида;

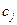– стоимость (иначе – доход от реализации) единицы товара j-го вида.

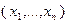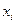Требуется найти стратегию, т.е. определить, сколько товаров каждого вида надо производить, чтобы обеспечить максимальный валовый доход от реализации. Искомую стратегию будем рассматривать в виде набора , где – количество товаров i-го вида, которое необходимо производить (i=1,…,n).

Целевой функцией 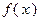является валовый доход

,

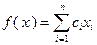а условиями

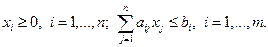
С учетом изложенного задача может быть сформулирована в виде:

;

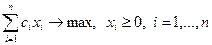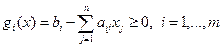
Данная задача относится к классу задач линейного программирования.

Задача № 2. Поиск объекта

Имеется n районов, в каком-то из них находится искомый объект (цель). Поиск осуществляет самолет в течение времени, которое не может превышать заданного значения T. Известны значения 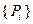вероятностей нахождения цели в каждом из районов (i=1,…,n). Вероятность (условная) обнаружения цели в i-м районе при условии, что цель находится в нем, задана выражением

,

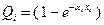причем значения 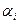известны, а 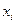(время поиска цели в i-м районе), i=1,…,n, являются величинами искомыми. Требуется определить набор значений ( 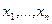), максимизирующий вероятность (безусловную) обнаружения цели.

Таким образом, задача может быть сформулирована в виде:

, , , .

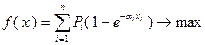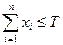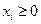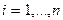Ограничения линейны, однако целевая функция нелинейна, поэтому нелинейной является и вся задача в целом. Рассмотренная задача относится к типу так называемых гладких задач, в данном случае за счет возможности дифференцировать экспоненциальную функцию неограниченное количество раз.

Задача № 3. Выбор системы вооружений

Рассматриваются два противника: A и B. A может создать m типов вооружений. Известно также, что единица вооружения i-го типа наносит противнику ущерб 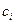, а стоимость создания единицы вооружения i-го типа равна 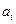. При этом военный бюджет стороны A равен 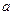. Требуется определить стратегию, т.е. набор 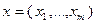значений количеств вооружений каждого типа, определяющий систему вооружений стороны A. В качестве целевой функции 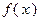выбираем ущерб, наносимый противнику, и задача записывается в следующем виде:

, , ,

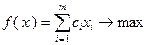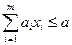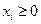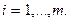
Достаточно легко найти решение этой задачи, которое обозначим через 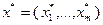. Для этого находим значение индекса 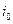, при котором

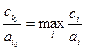. Тогда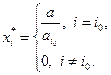

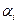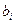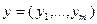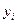Рассмотренную задачу можно усложнить, если учесть противодействие противника. Пусть – коэффициент уязвимости i-го средства нападения, – стоимость i-го средства противодействия (i=1,…,m), b – военный бюджет противника. Введем в рассмотрение набор значений , где – количество единиц средства противодействия против средства нападения i-го типа (i=1,…,m). Суммарный ущерб стороны B определим в виде:

.

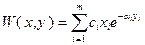При этом для ограничений можно записать:

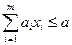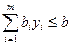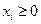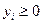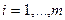, , , , . (1.3)

Если известен набор значений 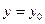, то решается задача 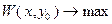. Если

набор 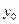неизвестен, то подобная задача решается методами исследования операций. Например, используется принцип гарантированного результата – расчет на наихудший ответ противника. В этом случае решается задача максимина:

,

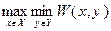где 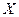, 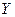– множества допустимых значений наборов (векторов) 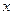и 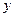, определяемые ограничениями (1.3).

Рассмотренная задача не является гладкой, так как. негладкой является функция

.

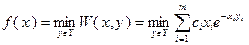Задача № 4. Оптимальное управление

Задачи оптимального управления возникают всюду, где существует возможность воздействовать на ход процесса. Это могут быть задачи управления движущимися объектами, технологическими процессами, процессами, происходящими в экономике и т.д. Далеко не безразлично, какими средствами будет достигнута цель управления тем или иным объектом. На практике всегда имеется определенный критерий качества, характеризующий «цену», которую приходится платить за достижение цели.

Математическая постановка задачи оптимального управления заключается в следующем. Задан объект, координаты которого описываются n-мерным вектором 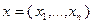. Координаты объекта изменяются во времени согласно системе дифференциальных уравнений

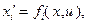
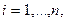(1.4)

где 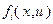– функции x и r-мерного вектора управления 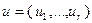. Вектор x, характеризующий положение объекта, называется вектором фазовых координат. Если задано начальное состояние объекта 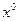и функция управления u(t), то при некоторых предположениях система (1.4) однозначно определяет траекторию объекта x(t), которая называется фазовой траекторией. Как правило, на управление u наложены некоторые ограничения. В общем случае они заключаются в том, что в каждый момент времени вектор u(t) должен принадлежать некоторому множеству U, которое является подмножеством r-мерного пространства. Пусть, кроме того, заданы начальная точка 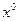и конечная точка 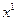фазового пространства. Рассмотрим все возможные управления u(t) и моменты времен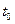и и 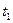, 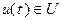для всех 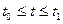, такие, что траектория x(t) системы (1.4), соответствующая начальному положению 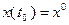и управлению u(t), попадает в момент времени 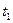в точку 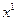, т.е. 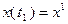. Среди этих управлений требуется выбрать одно, для которого значение функционала

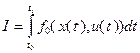
минимально. Управление и траекторию, являющиеся решением этой задачи, называют соответственно оптимальным управлением и оптимальной траекторией. Сформулированная задача является задачей выбора программного управления, так как здесь управление выбирается как функция времени.

В некоторых случаях физические соображения заставляют выбирать такое управление, чтобы соответствующая ему фазовая траектория удовлетворяла некоторым ограничениям. Например, 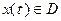, где D – некоторая область в n-мерном пространстве или вдоль траектории должно выполняться условие 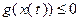, где g(x) – заданная функция. Условия типа 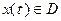или 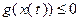носят название фазовых ограничений, а соответствующая задача – задачи оптимального управления с фазовыми ограничениями. Траектория системы (1.4), удовлетворяющая фазовым ограничениям, называется допустимой траекторией.

Одним из подходов к решению задач оптимального управления является динамическое программирование. Применение теории динамического программирования к решению задачи оптимального управления основано на том факте, что отрезок каждой оптимальной траектории также оптимален среди всех траекторий, соединяющих начальную и конечную точки отрезка.