Расчет на устойчивость статически неопределимых рам методом деформаций

При исследовании устойчивости рам принимаются допущения, значительно упрощающие вычисление критической нагрузки.

Во-первых, рассматриваем только узловую нагрузку, не вызывающую поперечного изгиба стержней рамы. Во-вторых, пренебрегаем продольными деформациями элементов рамы.

Поскольку продольно-поперечный изгиб рамы в момент критического равновесия характеризуется неизменной продольной силой, то при расчете рамы на устойчивость можем применить принцип независимости действия сил и воспользоваться, например, методом деформаций.

Выбор основной системы при расчете рам на устойчивость по методу деформаций ничем не отличается от выбора основной системы при обычном статическом расчете этим методом.

Так как мы рассматриваем рамы только с такой узловой нагрузкой, которая до момента потери устойчивости вызывает только сжатие (или растяжение) отдельных стержней, то реакции в дополнительных связях от нагрузки равны нулю и система канонических уравнений будет являться однородной системой уравнений:

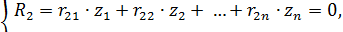(133)

Система этих уравнений позволяет найти лишь отношение неизвестных 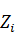, т.е. определить форму потери устойчивости.

Система уравнений удовлетворится, если положить все неизвестные равными нулю; это устанавливает отсутствие изгиба стержней рамы, чему соответствует устойчивое равновесие системы при силах, меньших критических.

Моменту потери устойчивости рамы (критическому состоянию) соответствует наличие изгиба элементов рамы, т.е. неравенство нулю неизвестных 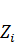. Этот случай возможен только тогда, когда детерминант системы (133), составленный из коэффициентов при неизвестных, равен нулю:

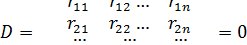(134)

Уравнение (134) является уравнением устойчивости при расчете сооружений по методу деформаций. Оно выражает условие критического равновесия системы. Отсюда можем найти спектр значений критической нагрузки. Каждому значению критической нагрузки соответствует своя форма потери устойчивости. Форму потери устойчивости, соответствующую минимальному значению критической нагрузки, будем называть опасной формой потери устойчивости.

Вычисление коэффициентов метода деформаций, т.е. реакций от единичных смещений дополнительных связей должно быть проведено с учетом влияния продольного изгиба.

Определение коэффициентов 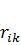метода деформаций

Рассмотрим сначала стержень, заделанный одним концом и шарнирно опертый другим. При повороте заделки на единичный угол в стержне возникают изгибающие моменты (рис.75).

Так как 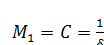, определим 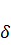- угол поворота от единичного момента (рис.75) по «обобщенной формуле трапеции»:

;

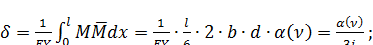
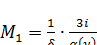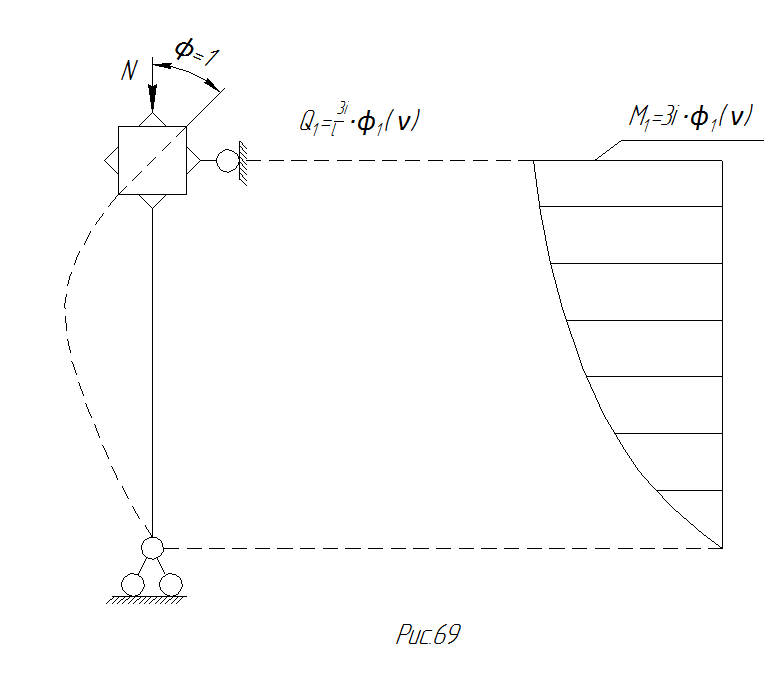
Рис. 75 Расчет стержня с помощью типовых эпюр

Обозначим 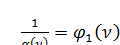, (135)

тогда .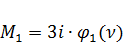

Заметим, что при 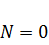, 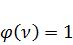и

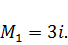
Поперечная сила определяется по формуле:

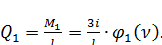(136)

При линейном смещении заделки той же балки на величину 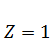в заделке возникает изгибающий момент , равный по величине поперечной силе , согласно теореме о взаимности реакций, то есть

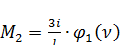(137)

Таким образом, реакции в заделке при повороте последней на угол, равный единице, с учетом влияния силы P, меньше реакции в простом стержне. Первая отличается от последней множителем 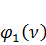, который меньше единицы (рис. 76).

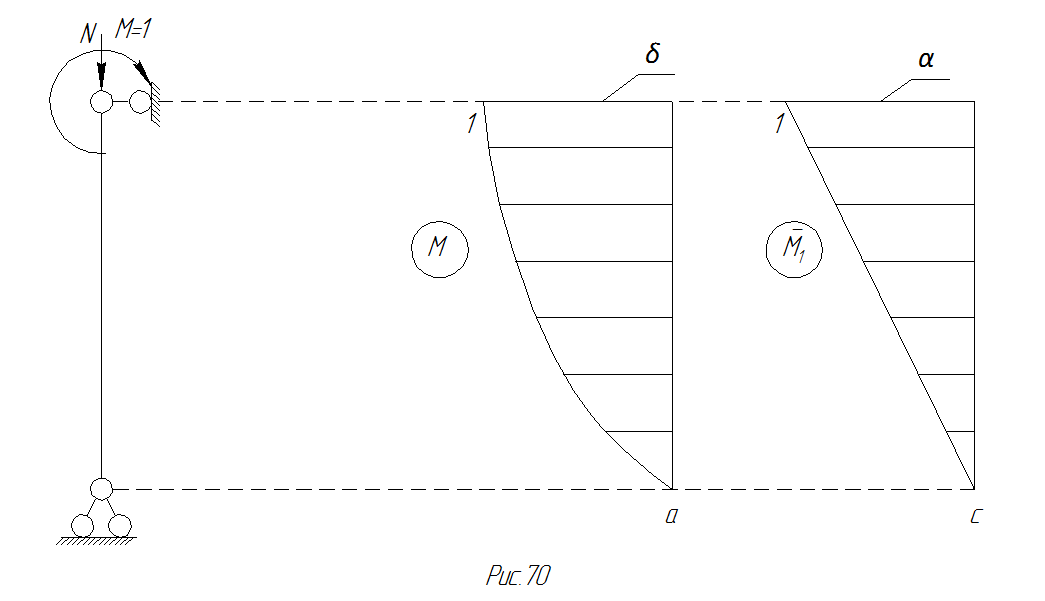
Рис. 76 Графики эпюр моментов М и М₁

Поперечную силу 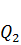найдем из условия равновесия моментов всех сил относительно шарнира A: (см. рис. 77).

,

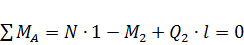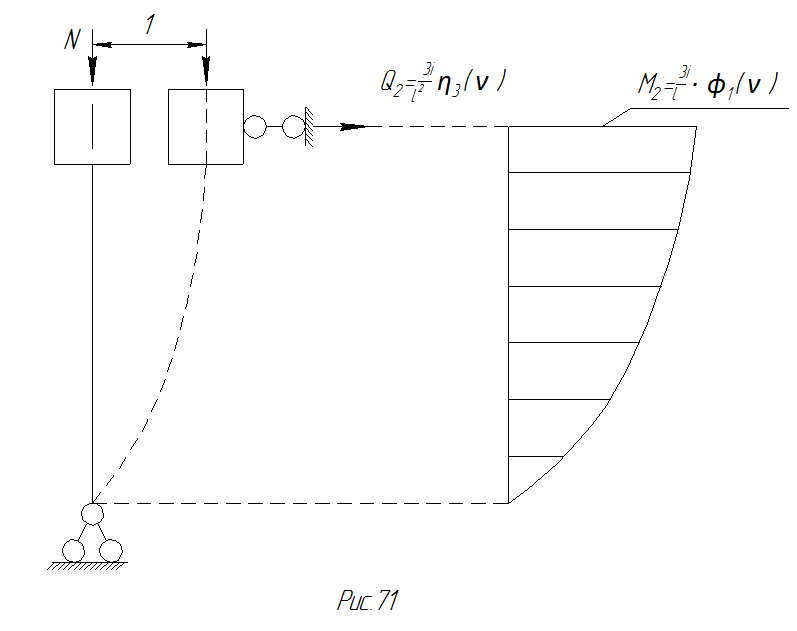
Рис. 77 Построение эпюры моментов, с помощью таблицы типовых эпюр

или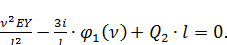

Откуда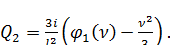

Обозначим 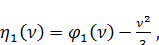(138)

тогда 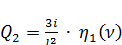. (139)

Отсюда видно, что поперечная сила при единичном смещении заделки сжатого стержня (рис.77) отличается от таковой же без учета сжатия поправочным множителем .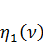

Аналогично можно показать, что и для стержня с заделанными концами моменты в заделках от поворота одной заделки на угол, равный единице, при учете влияния сжимающей силы определяются так же, как для стержня без учета сжатия, но с введением поправок множителям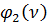и и 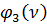(рис.78).

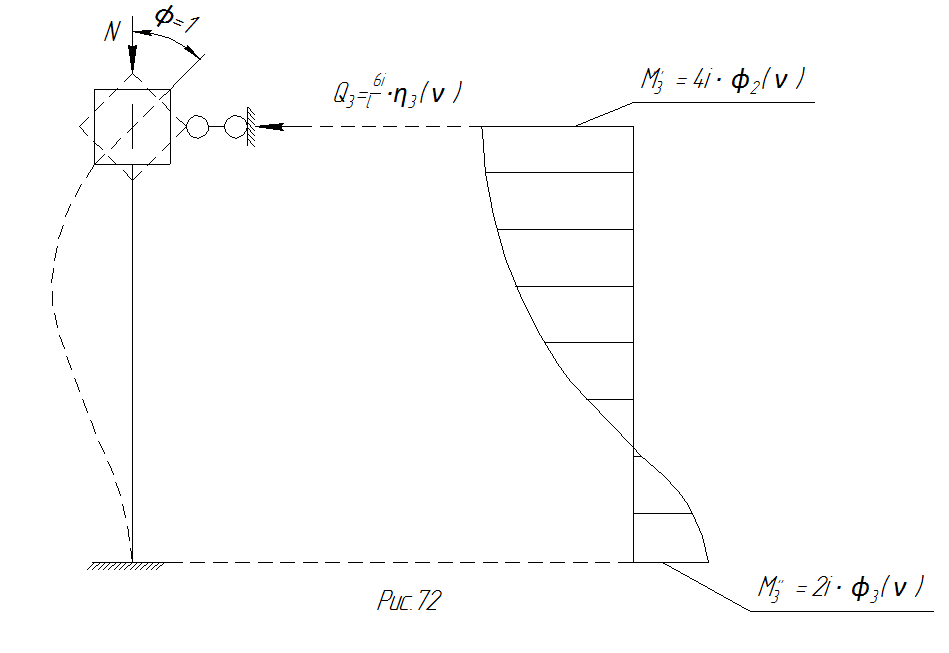
Рис. 78 Построение эпюры моментов, с помощью таблицы типовых эпюр

,

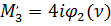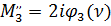(140)

От действия силы в раме возникает изгибающий момент М₄

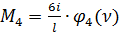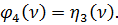, при (141)

При линейном смещении одной из заделок на единицу (рис.79) возникает изгибающий момент 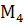, равный по величине силе 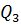,согласно теореме о взаимности реакций, т.е.

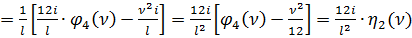(142)

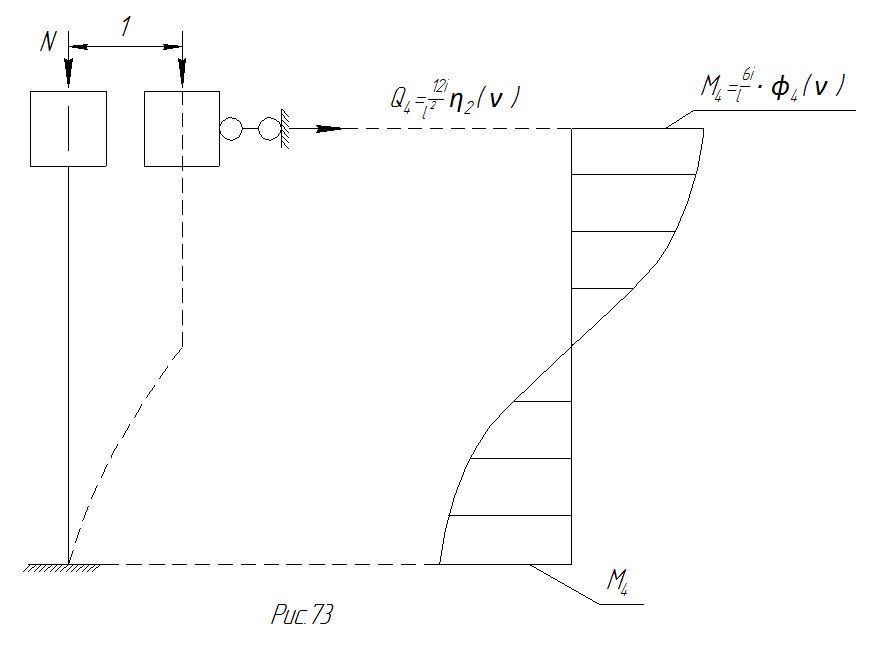
Рис. 79 Построение эпюры моментов, с помощью таблицы типовых эпюр

Условия равновесия моментов всех сил относительно точки А

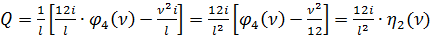(143)

При расчете рам методом деформаций на действие обычной статической нагрузки, приведенных выше четырех случаев определения реакции достаточно для составления канонических уравнений. В расчете на устойчивость рам к этим четырем случаям надо добавить пятый случай; расчет стержня, шарнирно опертого по концам. Для такого стержня необходимо определить поперечную силу (отнесенную к первоначальной силе).

Определим силу (см. рис. 80) 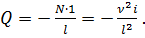(144)

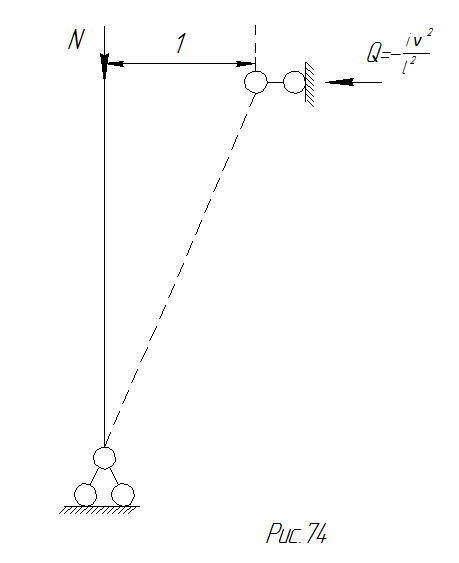
Рис. 80 Расчетная схема стержня при определении поперечной силы

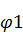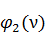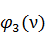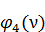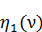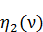Для удобства решения методом деформаций все поправочные множители: , (ν), , , , и , вычисленные для разных значений, приведены в таблице 1 приложения.