Оптимум фирмы, использующей два ресурса.

Теперь предположим, что фирма использует два ресурса (фактора) производства – труд (L) и капитал (K), приобретая их на конкурентном рынке по фиксированным ценам P_L и P_K. Используя эти факторы, фирма производит единственный продукт А и продаёт его на конкурентном рынке по цене P_A. Найдём условия, при которых данная фирма придёт в состояние оптимума.

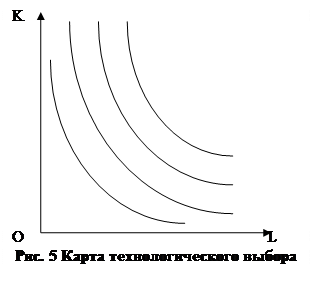Во-первых, построим карту технологических возможностей фирмы. Предположим, что факторы, которые использует фирма, обладают свойством бесконечной делимости. Тогда возможно бесконечное множество сочетаний этих двух факторов. Каждое такое сочетание – технология – позволяет произвести строго определённое количество блага. Существует множество технологий, позволяющих произвести одно и то же количество блага. Если все эти технологии объединить на графике, то мы получим кривую, которую называют изоквантой (от английского quantity– количество). Семейство изоквант изображено на Рис 5. Выпуклая форма изоквант свидетельствует об убывающей предельной норме замещения. Если, например, объём использования труда возрастает, то его продуктовая отдача становится все меньше и меньше. Напротив, отдача от всё меньшего числа единиц капитала становится больше. Поэтому для компенсации потери одной единицы труда потребуется всё меньшее количество капитала. Точное представление о норме замещения одного фактора другим (труда капиталом) даёт тангенс угла касательной, проведённой к соответствующей точке изокванты. Он показывает отношение предельного продукта труда к предельному продукту капитала в данной технологии. Чем дальше влево продвигаемся мы по изокванте, тем меньше становится угол касательной. Это означает, что предельный продукт труда становится всё меньше по сравнению с предельным продуктом капитала.

Из других свойств изоквант отметим два. Чем выше и правее расположена изокванта, тем больший объём блага способны произвести технологии, которые её составляют. Изокванты не имеют общих точек. В противном случае нам пришлось бы предположить, что одна и та же технология способна произвести два различных объёма блага, что противоречит логике.

Теперь определим ограничения, с которыми сталкивается фирма. Из условий следует, что таковыми являются бюджетные ограничения. Они могут быть записаны в виде

M_O = P_LQ_L + P_KQ_K

где M_O – денежный запас в распоряжении фирмы, а Q_L и Q_K– количества приобретаемых факторов. После небольшого преобразования мы получим уравнение бюджетной линии (эту линию называют изокостой от английского слово costs – издержки):

Q_K = M_O/P_K - Q_L P_L/P_K.

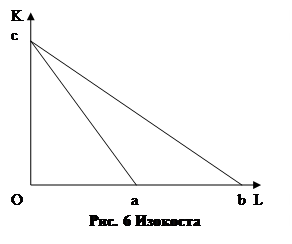
Очевидно, что представленное уравнение – ни что иное как уравнении линии с отрицательным наклоном (Рис. 6). Наклон изокосты всецело определяется соотношением цен на факторы производства. Если в исходном периоде цены капитал и труд определяли изокосту ac, то после того как единица труда подешевела вдвое, изокоста повернулась против часовой стрелки и заняла положение bc – при том же денежном запасе фирма может приобрести вдвое больше единиц труда. Мы будем исходить из предположения, что фирма полностью расходует свой денежный запас на приобретение факторов производства. Поэтому она будет находиться на изокосте. Если бы фирма часть денежного запаса сберегала, то находилась бы ниже изокосты. Все технологии, расположенные выше изокосты, для фирмы недостижимы.

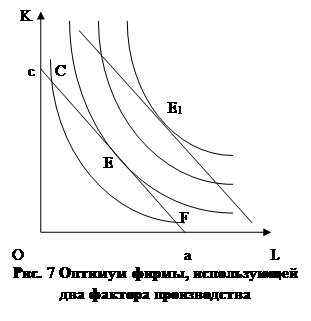
Теперь определим оптимум фирмы. Для этого совместим изокосту с картой технологического выбора как это показано на Рис. 7. Оптимуму будет соответствовать точка E, где изокоста касается изокванты. Технология, соответствующая точке касания, позволит фирме произвести максимальный объём продукта при заданном бюджете и ценах на факторы производства. Легко убедиться, что другие достижимые для фирмы технологии не удовлетворяет требованию максимума прибыли. Рассмотрим в качестве примера точки пересечения изокванты и изокосты C и F. Они не являются оптимальными, поскольку двинувшись по изокосте соответственно вверх или вниз фирма перейдёт к технологиям, позволяющим произвести больший объём блага при неизменных издержках. Лишь находясь в точке, Е фирма не может увеличить объём производства блага, а значит здесь объём производства максимален. Поскольку по условию фирма не влияет на цену производимого продукта, постольку максимуму производства продукта соответствует и максимальная выручка, а значит и максимум прибыли.

Рассмотрим условия оптимума фирмы. Она достигает максимума прибыли в тот момент, когда изокоста касается изокванты. Наклон касательной определяется соотношением цен на труд и капитал, а любая касательная характеризует соотношение предельных продуктов труда и капитала. Следовательно, в состоянии оптимума верно равенство:

P_L/P_K = MP_L/MP_K.

Это означает, что фирма достигает оптимума в тот момент, когда соотношение предельных продуктов факторов в точности равно соотношению их цен. Или, что то же самое, - фирма получит максимум прибыли тогда и только тогда, когда продуктовая отдача от рубля расходов одинакова, независимо от того, на какое благо потрачен этот рубль. То есть

MP_L/P_L = MP_K/P_K.

Действительно, если бы отдача от рубля, израсходованного на труд, превышала бы отдачу от рубля, истраченного на капитал, то фирма направляла бы расходы на труд. Но тогда предельная отдача от труда стала бы снижаться, а предельная отдача от капитала – расти. Естественно, что такое перераспределение доходов продолжалось бы до тех пор, пока отдача на рубль ни стала бы равной.

4. Отношения дополняемости и конкуренции в сфере производства[7].

Отношения дополняемости и конкуренции в сфере производства значительно сложнее, чем в сфере потребления. Действительно, необходимо принимать во внимание не только взаимосвязь между факторами производства, но также ещё и между факторами производства и производимыми с их помощью продуктами. Наконец, следует учесть, что иногда, используя один и тот же набор факторов, фирмы производят на его основе несколько продуктов. Отношения между этими продуктами могут быть как дополняющими, так и конкурирующими.

Сначала рассмотрим взаимоотношения между факторами производства. Предположим, что первоначально фирма сталкивалась с бюджетными ограничениями, формирующими изокосту са (Рис. 8). Тогда фирма получит максимум прибыли, используя технологию Е. Предположим, что в дальнейшем объём доходов, которым располагает фирма начинает увеличиваться? Тогда изокоста начнёт сдвигаться вверх параллельно самой себе, касаясь при этом более высоких кривых безразличия. Например, удвоение дохода фирмы на Рис. 7 приведёт к появлению новой оптимальной технологии Е₁. Очевидно, что новая технология включает в себя больший объём обоих факторов производства по сравнению со старой. Этот результат нельзя считать случайным. Между ресурсами в производственной сфере обычно наблюдаются отношения дополняемости: если фирма увеличивает объём использования одного фактора (труда), то это приведёт к увеличению предельной отдачи от второго фактора (капитала) и фирме будет выгодно приобретать капитал в большем объёме. Иными словами, с точки зрения фирмы оба фактора являются полноценными (оба они способствуют увеличению прибыли) и, став богаче, она увеличит объём использования как труда, так и капитала.

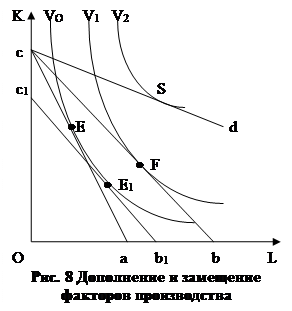Теперь предположим, что на рынке факторов производства произошли изменения другого рода – подешевел труд. Как показано на Рис. 8, удешевление труда приведёт к повороту изокосты против часовой стрелки в положение cb. Теперь уже изокоста коснётся более высокой изокванты. Это означает, что при новом соотношении цен фирма способна произвести больший объём продукта (V₁ вместо V_O), несмотря на то, что её издержки остались прежними по величине. Что мы можем сказать о новой оптимальной технологии F в сравнении с прежней технологией Е? Как мы видим, она включает большее количество труда и меньшее количество капитала. Значит ли это, что труд и капитал конкурируют между собой? Вовсе нет. Дело в том, что при удешевлении труда начинает действовать эффект замещения – подешевевший фактор производства (труд) начинает вытеснять из производства относительно подорожавший капитал. Этот эффект часто наблюдается в действительности. Например, удешевление труда в аграрном секторе СССР в 30-е годы ХХ века сделало невыгодным его механизацию. Однако при значительном удешевлении труда начинает сказываться действие эффекта дохода и фирма расширяет спрос на другие факторы производства, в том числе и на капитал. На Рис. 8 видно, что когда удешевление труда переводит изокосту в положение cd (фирма теперь может произвести V₁) возникает новая оптимальная технология S, которая включает в себя большее количество единиц обоих факторов.

Однако предположим, что наша фирма столкнулась с ограничениями. Вернёмся к случаю, когда удешевление труда привело к перемещению изокосты из положения ca в положение cb. Как мы отмечали выше, фирма может произвести больший объём блага, чем прежде. Но теперь предположим, что фирма столкнулась с ограничениями по спросу и не может продать блага больше, чем V_O. Это означает, что фирма не может покинуть соответствующую изокванту и оптимальная технология должна находиться на ней. Чтобы определить эту технологию мы должны построить изокосту c₁b₁, наклон которой определяется новым соотношением цен, но при этом касается она старой изокванты. Возникает новая оптимальная технология Е₁. В этой технологии подешевевший фактор (труд) однозначно вытесняет из производства относительно подорожавший фактор (капитал). Это означает, что если фирма столкнётся с какими-либо ограничениями, то отношения дополняемости между факторами производства немедленно сменятся на отношения конкуренции между ними.

В экономической теории принято анализировать поведение фирмы, производящей одно благо. Но в действительности преобладают фирмы, производящие несколько благ на основе использования одного и того же набора факторов производства. Между производимыми продуктами могут сложиться отношения как дополнения, так и конкуренции. Конкретная зависимость определяется чаще всего технологией. Дополнение возникает в том случае, если одни продукты является сопутствующими при производстве других. В качестве примера можно привести знаменитую задачу П. Самуэльсона о баранах[8]. Но очень часто фирма производит несколько не связанных между собой продуктов, используя для этого ограниченный запас ресурсов. В качестве простейшего примера мы можем привести работу магазина, который стеснён в торговых или складских площадях. Если магазин решит увеличить объём продаж продукта А, то ему придётся уменьшить продажи продукта В. В этом случае между продуктами возникнет конкуренция, поскольку использование ресурса для производства одного продукта означает отвлечение этого ресурса от производства другого. Если при дополнении производство одного продукта неизбежно приводит к увеличению другого, то при конкуренции увеличение объёма производства одного продукта означает, что другого продукта будет произведено меньше.

В заключение рассмотрим отношения между факторами производства с одной стороны и продуктами – с другой. Казалось бы это самый простой случай, поскольку увеличение объёма использования ресурсов обязательно должно вызвать увеличение объёма производства продукта. Такие отношения между ресурсом и продуктом свидетельствуют об отношениях дополнения. Но изредка наблюдается и обратная зависимость. Если подешевеет малопродуктивный ресурс, то фирма перенесёт свой спрос на него и в результате объём производства продукта сократиться. Такие конкурентные взаимоотношения между ресурсом и продуктом называются регрессией.