Оптимум потребителя при выборе товарного набора.

Предположим, что потребитель выбирает некоторую комбинацию, состоящую из двух благ X и Y. Цены благ известны, они равны соответственно P_X и P_Y. Уровень цен не зависит от объема приобретения блага со стороны данного покупателя. Определим товарный набор, который был бы оптимален по мнению самого покупателя. При анализе удобно воспользоваться методом кривых безразличия. Для этого необходимо выполнить три операции:

1. Определить поле выбора

2. Задать иерархию предпочтений покупателя («карта безразличия»)

3. Ввести ограничения, которые эффективно влияют на выбор покупателя, и совместить их с картой безразличия.

Y   E YE F     O XE X Рис. 25 Кривая безразличия потребителя

Рассмотрим теперь, как применяется этот метод кривых безразличия при отыскании оптимума потребителя, выбирающего из двух благ.

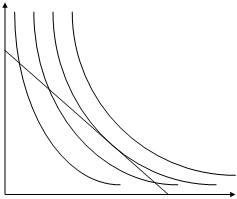
Предположим, что потребитель может выбрать любую комбинацию, состоящую из двух благ - X и Y. Тем самым мы уже определили поле выбора для него. На Рис. 25 поле выбора ограничено первым квадрантом. Теперь установим иерархию предпочтений потребителя. Любой точке в первом квадранте будет соответствовать строго определенный товарный набор. Например, в набор, задаваемый точкой Е, входит X_E товара X и Y_E товара Y. Этот товарный набор приносит потребителю некоторую полезность, равную U_E. Если допустить, что приобретаемые блага обладают свойством бесконечной делимости, то верно предположение о существовании множества наборов, отличающихся от данного набора Е по структуре, но приносящих потребителю точно такую же полезность. Действительно, исключим из первоначального набора Е часть товара Y - полезность набора уменьшится. Но эта потеря полезности может быть в точности компенсирована добавлением к набору соответствующего количества товара X. В результате в распоряжении потребителя останется набор F, полезность которого в точности равна полезности исходного набора Е. По условию таких равноценных с точки зрения потребителя наборов существует множество. Их совокупность представляет собой кривую, которая и получила название «кривая безразличия». Название это представляется весьма красноречивым - потребителю безразлично, какой из наборов, лежащих на данной кривой предпочесть, поскольку каждый из них принесёт ему одинаковую полезность.

Кривая безразличия выпукла вниз - это свидетельствует о действии закона убывающей предельной полезности. Согласно этому закону, полезность, приносимая потребителю каждой последующей порцией блага, меньше, чем полезность, приносимая предыдущей порцией. Чем меньше блага Y остаётся в распоряжении потребителя, тем большую потерю он будет ощущать, жертвуя новую его единицу, и тем больше единиц товара X потребует он в качестве компенсации за эту жертву. Точное соотношение такой замены определяется численным значением тангенса касательной, проведённой к точке, характеризующей данный товарный набор на графике. Это соотношение получило название «предельная норма замещения»; оно характеризует соотношение предельных полезностей товаров X и Y в данном товарном наборе, т.е. MU_X/MU_Y.

Аналогичным образом мы можем объединить все другие товарные наборы, попадающие на поле выбора. Иначе говоря, мы можем провести множество кривых безразличия, аналогичных той, что мы построили ранее. При этом чем выше и правее лежит кривая безразличия, тем большую полезность обеспечивают потребителю лежащие на ней товарные наборы.[4] Кривые безразличия не имеют друг с другом общих точек - в противном случае нам пришлось бы отказаться от гипотезы рациональности в поведении индивида, осуществляющего выбор. Действительно, если бы две кривые, соответствующие, как было сказано выше, двум различным уровням полезности, пересекались бы в некоторой точке, то это означало бы, что индивид одновременно присваивает одному и тому же товарному набору два уровня полезности.

Y     · N   · S   K ·     O X Рис. 26 Карта безразличия индивида

Совокупность кривых безразличия представляет собой так называемую «карту безразличия» (Рис. 26) - именно такой термин мы будем теперь применять вместо прежнего «поля выбора». Карта безразличия полностью описывает систему предпочтений индивида. Представим, что нам неизвестна карта безразличия, описывающая систему предпочтений индивида. В случае, если бы нам пришлось определять выбор индивида из пары наборов, подобной N и S , то отсутствие карты не имело бы значения. Очевидно, что рациональный индивид отверг бы набор S, поскольку тот заведомо приносит в этой паре меньшую полезность. Но наличие карты необходимо, когда выбор делается между наборами S и K. Только карта безразличия помогает определить, что индивид предпочтёт набор S.

Теперь введём в рассматриваемую систему ограничения, которые сковывают потребителя в процессе выбора. Предположим, что потребитель не способен повлиять на имеющийся в его распоряжении денежный запас (M_O) и на цены приобретаемых им товаров (P_X и P_Y). Тогда мы можем вывести бюджетное ограничение, которое запишется в виде:

(1) M_O = P_XX + P_YY,

где X и Y - физические количества приобретаемых благ. Преобразуя это уравнение, получим, что

(2) Y = M_O/P_Y - XP_X/P_Y.

Y   O X Рис. 27 Бюджетные ограничения покупателя

Поскольку все величины, за исключением X и Y - постоянные и не зависят от объёма приобретения блага со стороны покупателя, постольку полученное уравнение на графике будет отображаться прямой, имеющий отрицательный наклон (Рис. 3). Наклон полученной бюджетной линии всецело определяется соотношением цен на товары X и Y. Если, например, товар X подешевеет, то бюджетная линия станет положе. Бюджетная линия ограничивает собой область выбора, доступную для покупателя. Все комбинации благ, лежащие выше бюджетной линии, для покупателя недоступны, поскольку в его распоряжении нет достаточного количества денег.

Y     · D   · E   O X Рис. 28 Оптимум потребителя при выборе товарного набора

Теперь мы в состоянии определить товарный набор, который сам покупатель считает оптимальным. Для этого необходимо совместить бюджетную линию с картой безразличия, как это показано на Рис. 28. Оптимальным будет набор, которому соответствует Е - точка касания бюджетной линии с кривой безразличия. Легко убедиться, что находясь в любой другой точке, потребитель не будет достигать оптимума - в его распоряжении всегда будет возможность сформировать набор, приносящий большую полезность, чем имеющийся у него на руках. Если, например, в исходном периоде покупатель располагал набором D, то он может отказаться от некоторой части блага Y, заменив его на дополнительные единицы блага Х, что вызовет рост полезности товарного набора (это следует из того, что потребитель перешел на более высокую кривую безразличия). Но, находясь в точке E, потребитель уже не сможет улучшить товарный набор, поскольку он достиг наивысшей кривой безразличия. Любая попытка изменить структуру товарного набора обернётся для него уменьшением получаемой полезности, а на графике это выразится в сползании потребителя на более низкую кривую безразличия. Итак, оптимум потребителя достигается в тот момент, когда бюджетная линия коснется кривой безразличия, поскольку данная кривая - наивысшая из достижимых.

На основе проведённого анализа мы можем сформулировать основное правило оптимума. Мы выяснили, что наклон бюджетной линии определяется соотношением цен на покупаемые блага; в то же время нам известно, что любая касательная к некоторой точке характеризует соотношение предельных полезностей благ, входящих в соответствующий набор. Поскольку в точке, соответствующей оптимальному набору, оба эти условия соблюдаются, постольку будет верно следующее равенство:

(3) MU_X/MU_Y = P_X/P_Y,

что означает - в оптимальном товарном наборе соотношение предельных полезностей благ в точности равно соотношению их цен. Если мы преобразуем данное равенство, то получим, что

(4) MU_X/P_X = MU_Y/P_Y.

Полученное равенство свидетельствует о том, что набор может считаться оптимальным, когда каждый рубль расходов потребителя принесёт ему одинаковую полезность независимо от того, на какое именно благо этот рубль истрачен. В науке это правило известно как «второй закон Госсена». В своей работе «Эволюция, опубликованной ещё в 1854 году – задолго до официальной маржиналистской революции – Герман Генрих Госсен так сформулировал это правило: «Лицо максимизирует свою полезность, когда распределяет имеющиеся у него денежные средства между различными благами так, что достигает равного удовлетворения от последней единицы денег, потраченных на каждый из товаров».

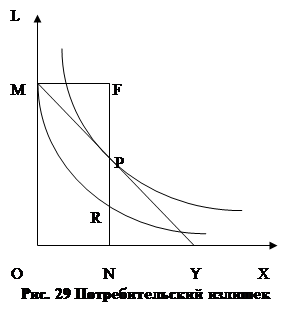
Теперь вернёмся назад и рассмотрим потребительскую премию в терминах кривых безразличия. Теория потребительской премии (потребительского излишка) была очень подробно исследована Альфредом Маршаллом в первом томе «Принципов политической экономии». Позже другой знаменитый экономист Джон Ричард Хикс в работе «Стоимость и капитал» адаптировал теорию потребительского излишка к методу кривых безразличия.[5] Предположим, что Некто делает выбор между покупкой некоторого объёма товара Х из денежного запаса L. По оси абсцисс отложим потенциальный объём товара Х, а по оси ординат – величину денежного запаса (Рис. 29). Бюджет покупателя представлен денежным запасом ОМ. Если он приобретает благо Х в объёме ON, то тратит на покупку денежную сумму в размере PF. Как определить размер потребительской премии? Для этого достаточно вспомнить, что потребительская премия есть денежная сумма, которую покупатель готов добавить к существующей цене лишь бы не остаться без данного запаса блага. Иными словами – это разница между той ценой, которую покупатель был готов заплатить за данное благо, и той ценой, которую он в действительности за него заплатил. Итак, когда в распоряжении покупателя вообще не было блага Х он находился в точке М. Если бы за ON блага он заплатил RF денег, то его благосостояние не претерпело бы изменений. В действительности, как мы видели, за данное количество блага он заплатил всего лишь PF денег. Отсюда следует, что покупатель согласился бы доплатить ещё RP денег, лишь бы получить в своё распоряжение ON блага. Указанная сумма и образует собой эквивалент потребительской премии (потребительского излишка).