МЕТОД ГАРМОНИЧЕСКОЙ ЛИНЕАРИЗАЦИИ
Гипотеза фильтра
Метод гармонической линеаризации для анализа систем автоматического управления предложен Л.С. Гольдфарбом в 1940 году. В его основе лежит аппроксимация колебательного движения системы первой гармоникой разложения в ряд Фурье периодической функции, описывающей это движение. Поэтому метод является приближенным. В некоторых случаях он позволяет исследовать устойчивость эталонного движения нелинейной системы, а также качественный характер её свободного движения.
Этот метод может быть применён для исследования систем любого порядка, но структура системы должна быть приведена к последовательному соединению нелинейного и линейного блоков. Чаще всего этим методом исследуется устойчивость положения равновесия системы. При определённых условиях можно установить наличие или отсутствие периодических движений, а также определить параметры последних, если эти движения существуют в системе.
Переходя к рассмотрению метода гармонической линеаризации, будем считать, что структурная схема исследуемой нелинейной системы приведена к виду, показанному на рис. 11.1.
Так как исследуется устойчивость системы, то внешнее воздействие 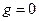 . Уравнения линейной части (ЛЧ):
. Уравнения линейной части (ЛЧ):
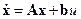 ,
, 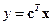 . (11.1)
. (11.1)
Далее будем считать, что линейная часть рассматриваемой системы стабилизируемая, т.е. её неполная часть асимптотически устойчива. Обозначим через Wл(р) передаточную функцию линейной части, соответствующую уравнениям (11.1), т.е.
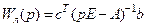 . (11.2)
. (11.2)
Нелинейный элемент (НЭ) может иметь любую характеристику z = Z(ε), лишь бы она была интегрируемой (т.е. без разрывов второго рода).
В основе метода гармонической линеаризации лежит следующее предположение: если исследуемая система неустойчива, то в ней могут возникать незатухающие периодические колебания. Это предположение позволяет считать, что переменная
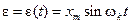 , (11.3)
, (11.3)
где 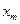
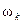 – амплитуда и частота колебаний, действующих на входе нелинейного элемента.
– амплитуда и частота колебаний, действующих на входе нелинейного элемента.
Для примера, преобразование переменной 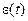 нелинейным элементом с зоной нечувствительности показано на рис. 11.2. Как видно, выходная переменная нелинейного элемента
нелинейным элементом с зоной нечувствительности показано на рис. 11.2. Как видно, выходная переменная нелинейного элемента 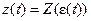 также является периодической функцией, т.е. её можно разложить в ряд Фурье с тем же периодом
также является периодической функцией, т.е. её можно разложить в ряд Фурье с тем же периодом 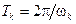 . Тогда будем иметь
. Тогда будем иметь
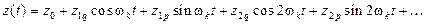 (11.4)
(11.4)
Здесь 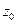 ,
, 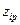 ,
, 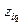 – коэффициенты ряда Фурье,
– коэффициенты ряда Фурье, 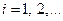 .
.
Далее делается второе, основное предположение данного метода – так называемая «гипотеза фильтра». Гипотеза фильтра состоит в предположении, что линейная часть с передаточной функцией (11.2) нелинейной системы (см. рис. 11.1) является фильтром нижних частот (ФНЧ). Другими словами, предполагается, что линейная часть подавляет все высшие гармоники с частотами 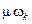 , начиная со второй, т.е. с
, начиная со второй, т.е. с 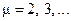 , и пропускает первую гармонику с частотой
, и пропускает первую гармонику с частотой 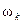 .
.
На рис. 11.3 показаны амплитудно-частотные характеристики A(ω) некоторых объектов управления. Причем объект с характеристикой, приведённой на рис. 11.3,а, не удовлетворяет гипотезе фильтра, а объект с характеристикой, приведённой на рис. 11.3,б, удовлетворяет гипотезе фильтра.
Так как в начале исследования частота колебаний ωk. неизвестна, то проверить выполнимость гипотезы фильтра до проведения расчёта нельзя. Поэтому приходится сначала провести все необходимые расчеты, а затем уже после определения частоты колебаний ωk проверить гипотезу фильтра. Если она окажется выполненной, то результаты расчетов будут соответствовать процессам, протекающим в исследуемой системе. Если же гипотеза фильтра не будет выполняться, то результаты расчетов не будут соответствовать процессам, протекающим в системе, т.е. метод гармонической линеаризации, изложенный ниже, применять для исследования такой системы нельзя.
Гармоническая линеаризация.В дальнейшем будем считать, что гипотеза фильтра выполняется, то есть все высшие гармоники сигнала, присутствующего на выходе нелинейного элемента, подавляются линейной частью системы, и поэтому они отсутствуют на выходе линейной части. В этом случае высшие гармоники можно отбросить и на выходе нелинейного элемента. В результате ряд (11.4) примет вид
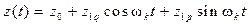 . (11.5)
. (11.5)
Если 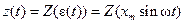 , то коэффициенты ряда Фурье периодической функции
, то коэффициенты ряда Фурье периодической функции 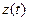 с периодом
с периодом 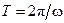 определяются по формулам
определяются по формулам
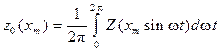 , (11.6)
, (11.6)

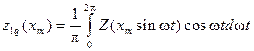 , (11.7)
, (11.7)
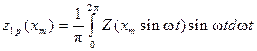 . (11.8)
. (11.8)
Представим равенство (11.5) в комплексной форме. С этой целью запишем очевидные равенства
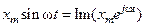 ,
,
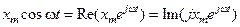 . (11.9)
. (11.9)
Отметим, что выражение вида 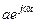 называется комплексом при любом
называется комплексом при любом 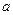 . С учетом равенств (11.6) – (11.9) выражение (11.5) принимает следующий вид:
. С учетом равенств (11.6) – (11.9) выражение (11.5) принимает следующий вид:
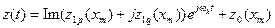 . (11.10)
. (11.10)
Обычно нелинейные характеристики являются симметричными относительно начала координат, поэтому чаще всего 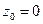 . Если
. Если 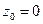 и выполняется гипотеза фильтра, то и на входе, и на выходе нелинейного элемента переменные, как видно из (11.3), (11.9) и (11.10), являются мнимыми частями соответствующих комплексов. Именно такая ситуация имеет место в случае линейных динамических звеньев. Поэтому нелинейный элемент рассматриваемой системы можно заменить линейным звеном.
и выполняется гипотеза фильтра, то и на входе, и на выходе нелинейного элемента переменные, как видно из (11.3), (11.9) и (11.10), являются мнимыми частями соответствующих комплексов. Именно такая ситуация имеет место в случае линейных динамических звеньев. Поэтому нелинейный элемент рассматриваемой системы можно заменить линейным звеном.
Комплексный коэффициент передачи любого линейного звена, по определению, равен отношению выходного комплекса звена к входному комплексу. По аналогии, в данном случае комплексный коэффициент передачи линейного звена, эквивалентного нелинейному элементу, определяется выражением
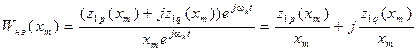
или
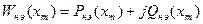 , (11.11)
, (11.11)
где
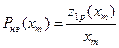 ,
, 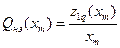 ,
,
где 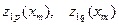 определяются выражениями (11.7) и (11.8).
определяются выражениями (11.7) и (11.8).
Величины 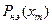 и
и 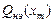 называются вещественным и мнимым коэффициентами гармонической линеаризации, а
называются вещественным и мнимым коэффициентами гармонической линеаризации, а 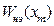 – коэффициентом гармонической
– коэффициентом гармонической
линеаризации.
Важнейшей особенностью коэффициентов гармонической линеаризации является то,
что они зависят не от частоты 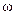 , как в линейном случае, а от амплитуды
, как в линейном случае, а от амплитуды 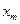 колебаний.
колебаний.
Рассмотренная процедура замены нелинейного элемента линейным звеном с ком-
плексным коэффициентом передачи (11.11) называется гармонической линеаризацией. Основное достоинство этой процедуры в том, что коэффициенты гармонической линеаризации 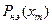 ,
, 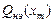 для заданной нелинейности
для заданной нелинейности 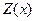 можно вычислять в символьной форме заранее. Для типовых нелинейностей эти коэффициенты вычислены и табулированы. Соответствующие выражения можно найти в литературе по теории автоматического управления или в приложении П.3, помещённом в конце настоящей книги.
можно вычислять в символьной форме заранее. Для типовых нелинейностей эти коэффициенты вычислены и табулированы. Соответствующие выражения можно найти в литературе по теории автоматического управления или в приложении П.3, помещённом в конце настоящей книги.
Для примера приведём здесь коэффициенты гармонической линеаризации некоторых наиболее часто встречающихся типовых нелинейностей.
В частности, для нелинейности, показанной на рис. 11.4, имеем
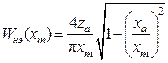 , (11.12)
, (11.12)
т.е. для этой нелинейности коэффициент гармонической линеаризации является вещественной функцией от амплитуды 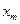 . Её график приведен на рис. 11.5.
. Её график приведен на рис. 11.5.
В случае нелинейности с положительным гистерезисом (рис. 11.6) коэффициент гармонической линеаризации определяется выражением
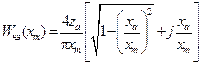 (11.13)
(11.13)
и является комплексной величиной. Графики вещественного 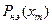 и мнимого
и мнимого 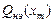 коэффициентов гармонической линеаризации этой нелинейности показаны на рис. 11.7.
коэффициентов гармонической линеаризации этой нелинейности показаны на рис. 11.7.
Для нелинейности типа идеальное реле (рис. 11.8), где зона нечувствительности 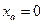 , коэффициент гармонической линеаризации принимает вид
, коэффициент гармонической линеаризации принимает вид
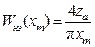 .
.
График этой функции приведен на рис. 11.9.
Коэффициенты гармонической линеаризации используются при исследовании нелинейных систем различных типов методом гармонической линеаризации.
Дата добавления: 2022-05-27; просмотров: 116;










