Построение временного процесса по фазовой траектории

В ряде случаев возникает необходимость построения зависимости от времени переменных состояния нелинейной системы по её фазовой траектории. Эту зависимость можно получить приближенно с помощью метода вписанных треугольников.

Для вывода основных соотношений этого метода рассмотрим отрезок фазовой траектории, показанный на рис. 10.30. Предположим, уравнения соответствующей нелинейной системы имеют вид

, .

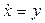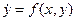Задача заключается в том, чтобы оценить время перехода изображающей точки из точки М₁

в близкую к ней точку М₂, т.е. необходимо оценить интервал .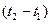

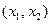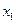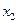Оценить указанный интервал точно по фазовой траектории сложно. Для его приближенной оценки из точек М₁ и М₂ (рис. 10.30), а затем и из середины отрезка , проводятся перпендикуляры к оси абсцисс. Точки и на оси соединяются прямыми линиями с серединой отрезка 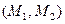фазовой траектории. В результате образуется равнобедренный треугольник с углом 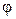при вершине.

Так как изменение ординаты 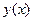при переходе из М₁ в М₂ невелико (при малом 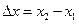), то её значение можно принять постоянным и равным значению в середине отрезка 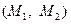, т.е.

, ,

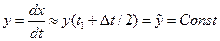где – приращение времени. Это выражение для переменной y можно представить следующим образом:

.

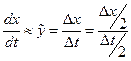Из этого выражения и свойств равнобедренных треугольников следует равенство

.

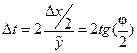На этом равенстве и основан метод вписанных треугольников, который заключается в следующем. Пусть задана точка 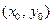, соответствующая времени 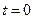. Тогда для построения зависимосте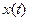й и 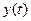необходимо выполнить следующие действия:

- задаться малым значением угла 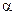(например, );

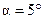- построить (рис. 10.31) равнобедренный треугольник с углом 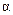при его вершине, лежащей на фазовой траектории. Боковое ребро этого треугольника должно пройти через точку 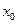, а биссектриса должна быть перпендикулярна к оси x. В результате получится точка ;

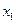- построить следующий треугольник с тем же углом 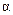. Вершина этого треугольника также должна лежать на фазовой траектории, биссектриса должна быть перпендикулярной к оси х, а левое ребро должно проходить через точку 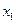(рис. 10.31). В результате получается следующая точка .

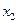Продолжая этот процесс, получают серию точек, соответствующих определенным моментам времени и координатам:

, , .

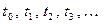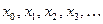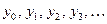При этом , , , 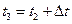а 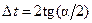. По полученным точкам строятся процессы 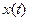и 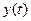(рис. 10.32).

В этом методе возникает некоторая сложность при переходе траектории через ось абсцисс. Поэтому после пересечения этой оси следующую точку на фазовой траектории выбирают так, чтобы время перехода в эту точку из предыдущей было приближённо равно .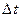

Г л а в а 11