Анализ фазовых траекторий в окрестности особых точек

Тип особой точки (определение которого является задачей данного параграфа) определяется характером фазовых траекторий, начинающихся в её малой окрестности. Для решения этой задачи можно воспользоваться известной теоремой Ляпунова, в которой утверждается, что если корни характеристического уравнения системы первого приближения, построенной в особой точке, не имеют нулевых вещественных частей, то характер движений нелинейной системы в малой окрестности этой точки определяется (совпадает с) характером движений линейной системы первого приближения. Это утверждение, очевидно, справедливо и в отношении характера тех фазовых траекторий нелинейных систем, которые начинаются в малой окрестности особой точки.

Таким образом, тип особой точки 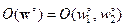фазового портрета нелинейной системы и соответственно характер фазовых траекторий, начинающихся в её окрестности, можно установить (по крайней мере, в указанном выше случае) методом линеаризации, т.е. с помощью уравнений первого приближения.

Построение уравнений первого приближения.Рассмотрим нелинейную систему, которая описывается уравнениями

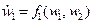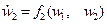, (10.7)

и имеет особую точку 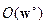, тип которой необходимо установить. С этой целью вводятся уравнения первого приближения данной системы, которые имеют вид

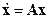. (10.8)

Коэффициенты 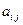матрицы 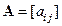вычисляются в особой точке 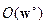по формулам

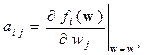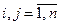, . (10.9)

Здесь 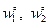– координаты особой точки. В уравнении (10.8) 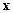– вектор отклонений переменных состояния от координат особой точки, т.е. .

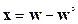Если фазовый портрет имеет несколько особых точек, то уравнение (10.8) строится по формулам (10.9) для каждой особой точки.

Пример 10.2.Нелинейная система

, ,

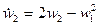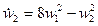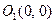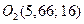
как показано выше, имеет особые точки , 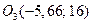. Найти уравнения первого приближения в окрестности точки .

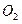Решение. В данном случае 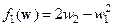, , 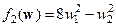поэтому по формулам (10.9) при 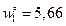, 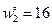находим

; ;

; .

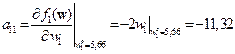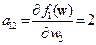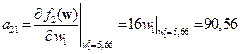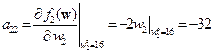Следовательно, согласно (10.8) и (10.9), уравнения первого приближения рассматриваемой системы в окрестности особой точки 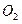имеют вид

. ■

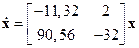Возвращаясь к задаче определения типов особых точек, запишем характеристическое уравнение системы первого приближения (10.8) следующим образом:

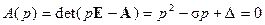. (10.10)

Его корни

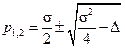. (10.11)

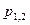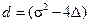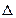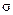Характер корней уравнения (10.10), как известно, зависит от знака дискриминанта этого уравнения. Поэтому рассмотрим плоскость параметров и (рис. 10.10) и построим на ней линию 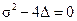. Эта линия вместе с координатными осями разбивает плоскость параметров 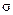и 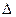на 5 областей, в каждой из которых корни 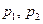(10.11) имеют различный характер. Рассмотрим характер фазовых траекторий для каждой из этих областей.

Область 1. Здесь 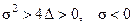, а корни 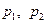– вещественные, различные, причём 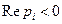, 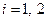. Характер траекторий в окрестности особой точки в этом случае показан на рис. 10.11. Фазовый портрет имеет два особых направления, соответствующих различным вещественным корням 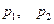. Данная особая точка называется «устойчивый узел».

Область 2.Здесь 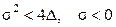, , 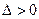а корни 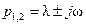– комплексные, причем 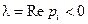, поэтому мода системы описывается выражением 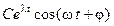, т.е. имеет затухающий колебательный характер. Одна из траекторий в окрестности соответствующей особой точки показана на рис.10.12. Особая точка называется «фокус». Это устойчивый фокус, так как траектории сходятся к особой точке при .

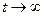Граница областей 1 и 2.Здесь 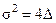, , 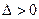а корни 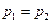причём 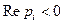. Так как оба корня равны друг другу, то фазовый портрет имеет лишь одно особое направление. Фазовый портрет для этого случая приведен на рис. 10.13. Особая точка называется устойчивым узлом, как и в области 1.

Граница областей 2 и 3.Здесь 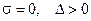, поэтому корни 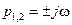чисто мнимые. Мода системы – 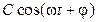. Ей соответствуют гармонические незатухающие колебания, амплитуда которых зависит от начальных значений переменных системы. Траектория, как отмечалось выше, называется циклом. Размеры цикла определяются начальными условиями 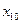, 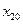. Фазовый портрет для этого случая приведен на рис. 10.14. Особая точка называется центром.

Область 3.Здесь 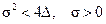, , 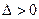а корни – комплексные, т.е. ,

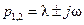причем 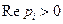. Поэтому фазовые траектории представляют собой расходящиеся спирали.

Фазовый портрет для этого случая приведен на рис. 10.15. Особая точка – фокус неустойчивый, так как траектории удаляются от особой точки.

Область 4.Здесь 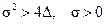, , 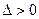а корни 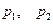– различные вещественные, причем 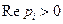. Так как имеется два различных вещественных корня, то на фазовом портрете имеется два особых направления. Фазовый портрет показан на рис. 10.16. Особая точка – неустойчивый узел.

Граница областей 3 и 4.Здесь 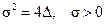, , 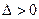а корни 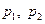– одинаковые, причем 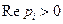. Следовательно, фазовый портрет имеет одно особое направление. Он приведен на рис. 10.17. Особая точка тоже – неустойчивый узел.

Области 5,а и 5,б.Здесь 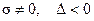, а корни 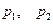– вещественные, различные; один из них положительный, а другой – отрицательный.

Фазовые траектории показаны на рис. 10.18. В области 5,а (см. рис. 10.10) модуль положительного корня больше, а в области 5,б больше модуль отрицательного корня. Поэтому в этих областях соответствующие сепаратрисы (особые направления) имеют разные наклоны (ср. рис. 10.18,а и рис. 10.18,б). Особая точка называется «седло». Это всегда неустойчивая особая точка.

Граница областей 5а и 5б.На рис. 10.10 эта граница обозначена а/б. Здесь 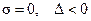, корни вещественные, равны по модулю и противоположны по знаку. Поэтому особые направления проходят под углами 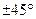. Фазовый портрет приведен на рис. 10.19. Особая точка тоже седло.

Граница областей 4 – 5а.Здесь 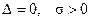, один корень равен нулю, а второй ра-

вен 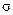и больше нуля. Поэтому фазовый портрет имеет вид, показанный на рис. 10.20. Особые точки занимают всю ось 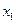, неустойчивы и названия не имеют.

Граница областей 1 и 5в.Здесь 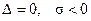, один корень равен нулю, а второй равен 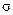и меньше нуля. Поэтому фазовый портрет линейной системы имеет вид, показанный на рис. 10.21. Особые точки занимают всю ось 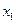, полуустойчивые, названия не имеют.

Подчеркнём, что указанные здесь виды особых точек и характер фазовых траекторий в их окрестностях соответствуют линейным системам вида .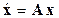

По отношению к нелинейной системе типа (10.7), для которой уравнение 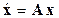является уравнением первого приближения в окрестности некоторой особой точки, можно, как отмечалось выше, утверждать, что указанные выше виды фазовых траекторий и типы особых точек имеют место, только в том случае, когда 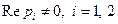. Другими словами, если характеристическое уравнение системы первого приближения, построенной в особой точке нелинейной системы, имеет хотя бы один корень с нулевой вещественной частью, то нельзя определить тип этой точки и характер фазовых траекторий в её окрестности путем анализа корней или коэффициентов характеристического уравнения линейной системы первого приближения.

Если же в окрестности особой точки нелинейной системы 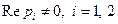, то тип этой особой точки и характер фазовых траекторий в её окрестности совпадает с типом особой точки и характером фазовых траекторий линейной системы первого приближения, построенной в этой точке.

Таким образом, фазовые траектории нелинейных систем в малых окрестностях особых точек чаще всего можно построить (изобразить) на основе численных значений корней или коэффициентов 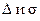характеристических уравнений соответствующих систем первого приближения.