Построение фазовых траекторий в большом

Для построения фазовых траекторий на большом удалении от особых точек (в большом) был разработан ряд графоаналитических методов. К ним относятся метод изоклин, дельта-метод, метод стыковки (припасовывания) и т. д. В настоящее время для этой цели целесообразно использовать либо метод припасовывания, либо численные методы приближенного решения нелинейных дифференциальных уравнений с помощью ЭВМ. Поэтому ограничимся здесь рассмотрением лишь метода припасовывания, так как он может с успехом применяться для аналитического исследования вручную различных нелинейных систем второго порядка.

Метод припасовывания.Этот метод применяется, если нелинейные уравнения содержат кусочно-линейные функции. При этом точки излома характеристик нелинейных элементов отображаются на фазовой плоскости в линии переключения. Эти линии делят фазовую плоскость на области, в которых уравнения нелинейной системы оказываются линейными, и есть возможность проинтегрировать уравнения фазовых траекторий. Далее, припасовывая (или стыкуя) друг к другу фазовые траектории из разных областей, получают фазовый портрет системы.

Последовательность построения фазового портрета методом припасовывания следующая.

1. Если система задана структурной схемой, то записать дифференциальные уравнения вход-выход системы в изображениях.

2. Перейти к уравнениям вход-выход в оригиналах.

3. Перейти к уравнениям в переменных состояния (x, y), исключив время t. Найти особые точки.

4. На основе условий изменения характера нелинейности сформировать уравнения линий переключения, и выделить области фазовой плоскости, в каждой из которых уравнения фазовых траекторий можно проинтегрировать. Найти выражение для в каждой i-й области.

5. Проинтегрировать уравнения фазовых траекторий и получить алгебраические уравнения фазовых траекторий 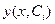для каждой i-й области. Здесь 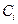– постоянные инте-

грирования.

6. Произвести припасовывание (стыкование) фазовых траекторий путем выбора постоянных интегрирования 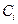. При этом начальные условия для последующего участка фазовой траектории будут равны координатам точки пересечения фазовой траектории предыдущего участка с линией переключения.

Для аналитического определения координат точек пересечения можно решать систему уравнений

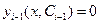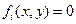, . (10.12)

Здесь 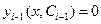– уравнение фазовой траектории предыдущего участка; 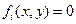– уравнение той линии переключения, к которой «подошла» фазовая траектория.

Пример 10.3.Рассмотрим построение методом припасовывания фазового портрета системы, показанной на рис. 10.22. Характеристика нелинейного элемента этой системы показана на этом же рисунке.

Решение. В соответствии с указанной выше последовательностью построения фазового портрета запишем по структурной схеме уравнения элементов системы в изображениях. В результате получим:

, ,

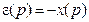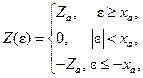
где 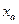– зона нечувствительности, 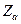– заданное число. Переходя к оригиналам, будем иметь

, .

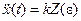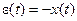Исключив отсюда промежуточную переменную 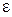и вводя обозначение 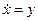, найдем, что уравнения системы имеют вид

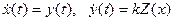, (10.13)

а нелинейность описывается выражениями

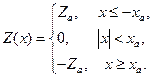(10.14)

В данном случае из условий, определяющих точки изменения значения нелинейности (точки разрыва нелинейной характеристики (10.14)), вытекают следующие уравнения линий переключения: 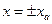. Соответствующие линии переключения показаны на рис. 10.23. На этом рисунке области, на которые линии переключения делят фазовую плоскость, показаны римскими цифрами I, II и III. Деля второе уравнение 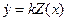системы (10.13) на первое, найдём, что фазовые траектории определяются выражением:

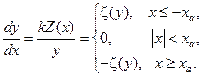(10.15)

где . Разделяя переменные в уравнениях (10.15) для I и III области и интегрируя, получим

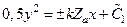
или

, (10.16)

где , 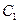– обозначения постоянной интегрирования. Причём для области I в этом равенстве необходимо брать знак «+», а для области III – знак «–». Аналогично для области II будем иметь

.

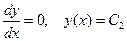Перейдём к построению фазового портрета. Для этого зададим начальную точку 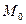, как показано на рис. 10.23.

По рисунку находим её координаты 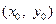. Так как начальная точка лежит в третьей области, то, согласно (10.16), уравнение фазовой траектории имеет вид

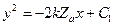, (10.17)

где неизвестная постоянная 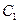определяет соответствующую фазовую траекторию. Поскольку искомая фазовая траектория проходит через точку 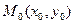, то её координаты удовлетворяют уравнению (10.17). Поэтому, подставляя 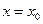и в (10.17), получим

.

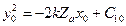Отсюда находим значение постоянной интегрирования

.

Подставляя это значение 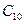в равенство (10.17) вместо 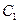, получим

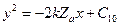(10.18)

– уравнение фазовой траектории, выходящей при 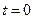из точки .

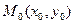Для построения собственно траектории задаёмся рядом значений 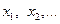и вычисляем по (10.18) соответствующие значения 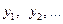. По полученным точкам строим фазовую траекторию. Когда эта фазовая траектория пересекается с линией переключения (на рис. 10.23 это происходит в точке 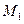), сменяются уравнения фазовой траектории. В данном случае после переключения фазовая траектория попадает в область II, где уравнение фазовых траекторий имеет вид 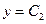. Для определения постоянной найдем сначала координаты точки пересечения фазовой траектории 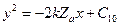из предыдущей области с линией переключения , решив систему (10.12). Это, очевидно, будет показанная на рис. 10.23 точка 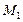с координатами .

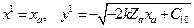Следовательно , а уравнение фазовой траектории в области II имеет вид . Это прямая, параллельная оси абсцисс. Проведя её до пересечения со второй линией переключения 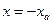, найдем координаты новой точки пересечения 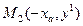. После переключения изображающая точка попадает в область I, где уравнения фазовых траекторий, согласно(10.16), определяются выражением 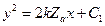. Здесь 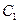– новая постоянная интегрирования. Подставляя в это уравнение координаты точки 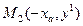, получим 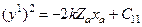– равенство для определения постоянной интегрирования 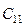. Следовательно, уравнение рассматриваемой фазовой траектории в области I имеет вид .

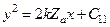С помощью этого уравнения можно построить фазовую траекторию в области I (между точкам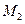и и 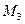на рис. 10.23), а затем продолжить её во второй и в третьей областях. Легко убедиться, что в данном случае продолжение рассматриваемой траектории пройдёт через начальную точку 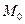, т. е. данная траектория является замкнутой кривой.

Повторяя описанные действия для других значений координат начальных точек, построим другие фазовые траектории, которые являются непредельными циклами. В итоге получим фазовый портрет рассматриваемой системы, показанный на рис. 10.23. ■

Аналогично строятся фазовые портреты для нелинейных систем с другими видами кусочно-линейных характеристик. На рис. 10.24 и рис. 10.25 приведены некоторые типы релейных характеристик, близких к приведенной на рис. 10.22, и фазовые портреты системы, приведённой на рис. 10.22, с этими нелинейностями.

Как видно, в случае знаковой нелинейности, в которой отсутствует зона нечувствительности (рис. 10.24), на фазовом портрете отсутствует область, в которой фазовые траектории идут параллельно оси абсцисс. Однако траектории и в этом случае являются замкнутыми непредельными циклами. Следовательно, в замкнутой системе и в этом случае наблюдаются периодические колебания, амплитуда которых зависит от начальных условий системы. Будет ли начало координат особой точкой – зависит от свойств знаковой нелинейности при .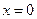

Отметим, что поскольку указанные колебания возникают в системе при отсутствии внешних воздействий, т.е. они порождаются самой системой, то они называются автоколебаниями.

В то же время, если вместо однозначной нелинейности включить в систему (рис. 10.22) релейную двухзначную нелинейность с положительным гистерезисом, фазовые характеристики становятся разомкнутыми, спиралевидными и расходящимися, как показано на рис. 10.25. Это свидетельствует о том, что при такой нелинейности в рассматриваемой системе возникают колебания с увеличивающейся амплитудой. При включении нелинейности с отрицательным гистерезисом колебания в системе будут затухающими.