Длительная прочность древесины

Древесина – реономный материал. При быстром возрастании и
кратковременном действии нагрузок древесина сохраняет 
упругость и деформируется сравнительно мало. При длительном действии неизменной нагрузки деформации во времени существенно увеличиваются. Если задать древесине неизменную во времени деформацию, например, определенный прогиб изгибаемому элементу, то напряжения с течением времени несколько уменьшаются - релаксируют, хотя деформация не изменяется.

Реологические свойства древесины учитываются при назначении расчетных сопротивлений. Под действием постоянной нагрузки непосредственно после ее приложения в древесине появляются упругие деформации, а с течением времени развиваются эластические и остаточные деформации. Упругие и эластические деформации обратимы - они исчезают после снятия нагрузки в течение малого (упругие деформации) или более или менее длительного (эластические деформации) промежутка времени. Остаточные деформации, являющиеся необратимой частью общих деформаций, остаются и после снятия нагрузки.

На прочность древесины значительно влияют скорость приложения нагрузки или продолжительность ее действия. Если серию одинаковых деревянных образцов загрузить, например, на изгиб, различной по значению постоянной нагрузкой, то разрушение их произойдет через разные промежутки времени: чем больше нагрузка (напряжение), тем скорее разрушится образец. При этом может оказаться, что часть образцов вообще не разрушится, как бы долго нагрузка ни действовала.

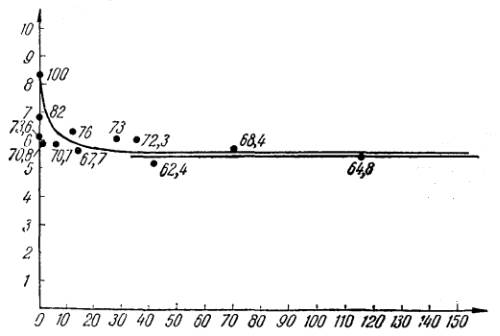
Представив результаты таких испытаний графически в координатах «предел прочности - время до разрушения» (рис.1), получим асимптотическую кривую, по которой можно определить, сколько времени пройдет от начала нагружения до разрушения образца, находящегося под тем или иным напряжением. Асимптотический характер кривой показывает, что предел прочности с увеличением длительности приложения нагрузки хотя и падает, но не безгранично, он стремится к некоторому постоянному значению σ_дл, равному ординате асимптоты кривой. Кривая на рис. 1, полученная Ф.П. Белянкиным, исследовавшим длительную прочность в 30-40-е годы прошлого века, называется кривой длительного сопротивления древесины, а ордината σ_дл - пределом длительного сопротивления древесины; σ_дл характеризует то предельное
(максимальное) значение напряжения (или нагрузки), под действием которого образец не разрушится, как бы долго нагрузка ни действовала. Длительное сопротивление называют также долговременной или длительной прочностью.

Rвр, кН/см2 (предел прочности - временное сопротивление)
	Т, сутки
Время выдержки образцов под постоянной нагрузкой до 4 месяцев
Рисунок 1 - Кривая длительной прочности древесины на изгиб, кратковременная прочность Rкр = 8,3 кН/см2 = 83 МПа   Из книги:Белянкин Ф.П. Современные методы расчета прочности элементов деревянных конструкций. // Киев: Изд-во АН УССР, 1951. – 19 с.
Числа возле точек графика означают прочность в % от стандартной, полученной при кратковременном машинном испытании чистых образцов (условно Т ≈ 0) и принятой за 100 %.

В современных учебниках схематично кривую длительного сопротивления показывают как на рисунке 2 без ссылок на авторство. Но главное здесь то, что эта кривая приведена для продолжительности выдержки под нагрузкой примерно в течение 4-х месяцев, а далее рассматривается длительность действия нагрузок до 50 лет.

Рисунок 2. Кривая длительного сопротивления древесины

Асимптота на кривой длительного сопротивления рис. 2 делит весь диапазон нагрузок на две части - область ниже асимптоты с σ < σ_дл = 62 МПа, в которой разрушение образца не произойдет, как бы долго ни действовала нагрузка, и область выше асимптоты с σ > σ_дл, где разрушение с течением времени неизбежно и где оно произойдет тем скорее, чем больше постоянное напряжение σ превышает σ_дл. Асимптотический характер кривой длительного сопротивления справедлив для всех видов напряженного состояния древесины (см. далее рис. 4).

Две области кривой, указанные на рис. 2, различают также по характеру зависимости деформации от времени при заданном значении действующей нагрузки (напряжения), что видно на рис. 3.

Это две кривые ползучести: затухающей (рис. 3а) и незатухающей (рис. 3б). Так, при напряжении σ < σ_дл деформации с течением времени затухают, стремясь к некоторому пределу (асимптота на
рис. 3а), а при σ > σ_дл после некоторого уменьшения скорости деформаций на участке в-г (рис. 3б) наступает развитие деформаций с постоянной скоростью на участке г-д. Далее, в момент времени t₁ начинается ускоренный рост деформаций, завершающийся разрушением материала.

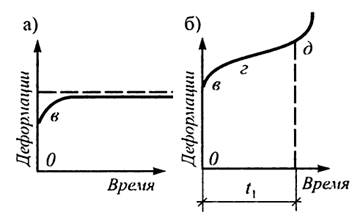
Рисунок 3 Кривые ползучести древесины

а – при σ < σ_дл; б – при σ > σ_дл

Как видно из рис. 3, древесина обладает свойством последействия (ползучести), т.е. роста деформаций в течение некоторого времени после приложения нагрузки. Примером последействия может служить провисание балок, находящихся долгое время под эксплуатационной нагрузкой.

Длительное сопротивление σ_дл является показателем действительной
прочности древесины в отличие от кратковременного предела прочности R_кр, определяемого быстрыми испытаниями на машине стандартных образцов. Переход от предела
прочности к длительному сопротивлению, соответствующему характерному времени действия нагрузок разных типов, производится умножением предела прочности на коэффициент длительного сопротивления m_дл, равный отношению предела длительного сопротивления σ_дл к пределу кратковременной (стандартной) прочности R_кр.