Изостатические редукции

При обработке геодезических данных возникла мысль о возможности улу­ч­ше­ния результатов при помощи учета действия избытка масс (горных соору­жений) и недостатка масс (глубоких впадин, прогибов). Для согласованности гео­дезических измерений была сформулирована гипотеза изостазии, или гипо­теза равновесного состояния земной коры.

Практически одновременно были сформулированы Праттом и Эйри две гипо­те­зы.

В основе гипотезы Пратта лежит предположение, что в Земле на глубине (T - поверхность компенсации) имеется поверхность, во всех точках которой дав­ле­­ние действует с одинаковой силой.

Гипотеза Эйрасостоит в следующем, что в некотором объеме земная кора одинаковой плотности (s > 0) и под корой лежит некий субстрат (s < 0), на котором она как бы плавает. Изменение поверхности компенсации изменяется следующим образом: под горами она увеличивается, под океанами - уменьшается. В основе этой гипотезы лежит закон Архимеда.

Гипотеза Венинг-Мейнеса. В основе ее лежит предположение, что земная кора - это упругая пластина бесконечного простирания (явление это не локальное, а региональное). При такой формулировке учитываются силы сцепления между отдельными колонками земной коры. Топографические массы представляют нагрузку, от которой пластина дает прогиб на границе компенсации, вытесняя более плотное вещество субстрата. Эта гипотеза остается на сегодняшний день самой жизнеспособной.

Рис. модельный пример региональной изостазии региональной.

Изостатические редукции

При введении в наблюденные значения силы тяжести изостатические редукции выделяются, среди которых следующие - это поправки за топографию и за компенсацию. Причем, притяжение внешних или топографических масс вычитается, а поправка за компенсацию, т.е. компенсирующие массы, прибавляется. Само собой разумеется, что поправки за свободный воздух также учитываются.

Вычисление этих поправок производится с помощью палеток по методике Хейфорда. При вычислении поправок учитывают следующие условия:

1) – поверхность компенсации относительно уровня моря на глубине 113,7 км;

2) 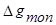– компенсация рельефа осуществляется полностью или локаль­но;

3) средняя плотность топографических масс равна 2,67 ^г/_см³

При высокоточечных гравиметрических измерениях необходимо вводить поп­равки за притяжение Луны и Солнца, которые могут создавать упругий прилив, при этом фигура Земли деформируется как бы вытягиваясь в эллипсоид с большей осью, направленной в сторону Луны. Принято называть этот эллип­соид приливным. Максимальная амплитуда этого прилива составляет 0,25 м.

Вли­яние солнечно-лунного притяжения учитывается по специально созданным графикам. Максимальная поправка за притяжение Луны составляет 0,25 мГал, а Солнца - 0,1 мГал.