Работа внешних сил при вращательном движении твердого тела.
Найдем работу, которую совершают силы при вращении тела вокруг неподвижной оси Z.
Пусть на массу 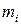 действуют внутренняя сила
действуют внутренняя сила 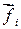 и внешняя сила
и внешняя сила 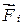 (результирующая сила
(результирующая сила 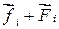 лежит в плоскости, перпендикулярной оси вращения) (рис. 4.19). Эти силы совершают за время dt работу:
лежит в плоскости, перпендикулярной оси вращения) (рис. 4.19). Эти силы совершают за время dt работу:
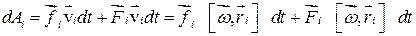 .
.
Осуществив в смешанных произведениях векторов циклическую перестановку сомножителей, находим:
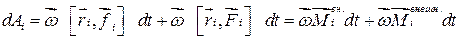 ,
,
где 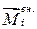 ,
, 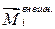 – соответственно, моменты внутренней и внешней сил относительно точки «О».
– соответственно, моменты внутренней и внешней сил относительно точки «О».
Просуммировав по всем элементарным массам, получим элементарную работу, совершаемую над телом за время dt:
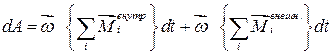 .
.
Сумма моментов внутренних сил равна нулю. Тогда, обозначив суммарный момент внешних сил через 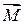 , придем к выражению:
, придем к выражению:

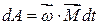 .
.
Известно, что скалярным произведением двух векторов называется скаляр, равный произведению модуля одного из перемножаемых векторов на проекцию второго на направление первого, учтя, что 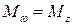 , (направления оси Z и
, (направления оси Z и 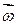 совпадают), получим
совпадают), получим
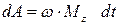 ,
,
но w·dt=dj, т.е. угол, на который поворачивается тело за время dt. Поэтому
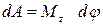 .
.
Знак работы зависит от знака Mz, т.е. от знака проекции вектора 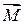 на направление вектора
на направление вектора 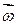 .
.
Итак, при вращении тела внутренние силы работы не совершают, а работа внешних сил определяется формулой 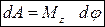 .
.
Работа за конечный промежуток времени находится путем интегрирования
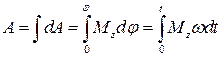 .
.
Если проекция результирующего момента внешних сил на направление 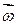 остается постоянной, то ее можно вынести за знак интеграла:
остается постоянной, то ее можно вынести за знак интеграла:
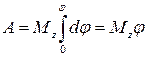 , т.е.
, т.е. 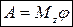 .
.
Т.е. работа внешней силы 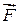 при вращательном движении тела равна произведению проекции момента внешней силы на направление
при вращательном движении тела равна произведению проекции момента внешней силы на направление 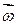 и угол поворота.
и угол поворота.
С другой стороны работа внешней силы, действующей на тело идет на приращение кинетической энергии тела (или равна изменению кинетической энергии вращающегося тела). Покажем это:
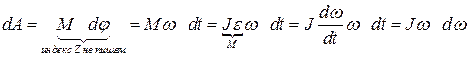
и тогда
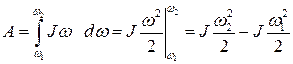 ;
;
Следовательно,
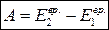 . (4.7)
. (4.7)
Самостоятельно:
Упругие силы;
Закон Гука.
| ЛЕКЦИЯ 7 |
Гидродинамика
Дата добавления: 2016-11-04; просмотров: 2153;











