Решение неопределенных уравнений при помощи алгоритма Евклида
Определение 6.1. Неопределенным уравнением будем называть уравнение вида 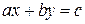 , где
, где 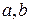 и
и  – коэффициенты уравнения, а буквами
– коэффициенты уравнения, а буквами 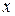 и
и 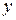 обозначены неизвестные величины. При этом предполагается, что
обозначены неизвестные величины. При этом предполагается, что 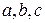 – целые числа, отличные от 0. Решить неопределенное уравнение, значит найти такие целые числа, которые будучи подставленными вместо неизвестных величин
– целые числа, отличные от 0. Решить неопределенное уравнение, значит найти такие целые числа, которые будучи подставленными вместо неизвестных величин 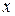 и
и 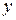 , превращают уравнение в верное числовое равенство.
, превращают уравнение в верное числовое равенство.
Частный случай. Рассмотрим частный случай неопределенного уравнения, когда правая часть уравнения равна 1:
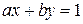 (6.1)
(6.1)
Заметим, что по теореме 5.1, это уравнение имеет решение только в случае, когда 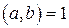 . Пусть
. Пусть 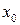 ,
, 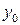 – одно из решений уравнения (6.1). Тогда любая пара целых чисел
– одно из решений уравнения (6.1). Тогда любая пара целых чисел 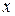 и
и 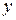 , вычисляемых по формулам
, вычисляемых по формулам
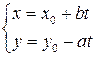 (6.2),
(6.2),
где 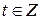 , также является решением уравнения (6.1). Действительно,
, также является решением уравнения (6.1). Действительно,
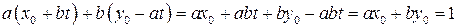 .
.
Пара чисел, вычисленных по формулам (6.2), называется общим решением уравнения (6.1), при этом говорят, что числа 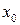 ,
, 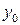 составляют частное решение данного уравнения.
составляют частное решение данного уравнения.
Докажем, что множество решений уравнения (6.1) состоит только из чисел, полученных из некоторого частного решения 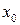 ,
, 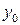 при помощи формул (6.2).
при помощи формул (6.2).
Пусть 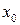 ,
, 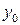 – некоторое частное решение уравнения (6.1), а
– некоторое частное решение уравнения (6.1), а 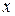 ,
, 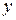 – также решение этого уравнения. Тогда
– также решение этого уравнения. Тогда
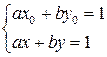 – верные равенства.
– верные равенства.
Следовательно, 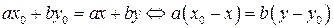 . Последнее равенство означает, что
. Последнее равенство означает, что 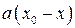
 b. Поскольку
b. Поскольку 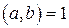 , имеем
, имеем 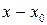
 b (по следствию 2 к теореме о необходимом и достаточном условии взаимной простоты двух чисел ), а это и означает, что
b (по следствию 2 к теореме о необходимом и достаточном условии взаимной простоты двух чисел ), а это и означает, что 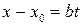 , где
, где 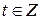 . Значит,
. Значит, 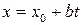 , где
, где 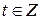 .
.
Подставим 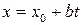 в уравнение (6.1). Получим, что
в уравнение (6.1). Получим, что
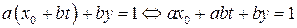 .
.
Но
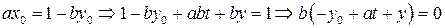 .
.
Поскольку  (по определению неопределенного уравнения),
(по определению неопределенного уравнения), 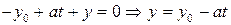 .
.
Требуемое утверждение доказано.
Примеры.
1) Решим уравнение 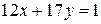 . Очевидно, что
. Очевидно, что 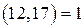 , значит уравнение имеет решение. Найдем НОД чисел 12 и 17 (который, как нам известно, равен 1) при помощи алгоритма Евклида. Для этого разделим
, значит уравнение имеет решение. Найдем НОД чисел 12 и 17 (который, как нам известно, равен 1) при помощи алгоритма Евклида. Для этого разделим 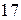 на
на 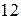 , получим
, получим 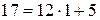 . Таким образом, первый полученный остаток
. Таким образом, первый полученный остаток 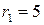 .
.
Далее, разделим 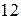 на
на 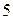 , получим
, получим 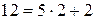 , при этом
, при этом 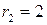 .
.
Продолжим процесс деления:
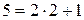 ,
, 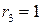 ;
;
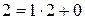 ,
, 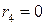 .
.
Таким образом, последний отличный от 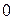 остаток равен 1, это и есть наибольший общий делитель чисел
остаток равен 1, это и есть наибольший общий делитель чисел 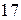 и
и 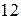 . Найдем линейное представление НОД:
. Найдем линейное представление НОД:
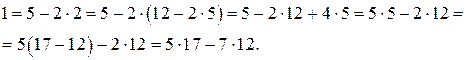
Таким образом, получим частное решение: 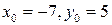 . Тогда общее решение этого уравнения имеет вид:
. Тогда общее решение этого уравнения имеет вид: 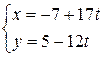 , где
, где 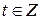 .
.
Общий случай. В общем случае правая часть неопределенного уравнения может быть любым целым числом:
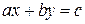 . (6.3)
. (6.3)
Пусть 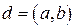 – наибольший общий делитель чисел
– наибольший общий делитель чисел  и
и  . Это значит, что
. Это значит, что 
 d и
d и 
 d. Поэтому для того, чтобы уравнение (6.3) имело решение необходимо и достаточно, чтобы
d. Поэтому для того, чтобы уравнение (6.3) имело решение необходимо и достаточно, чтобы 
 d.
d.
Пусть 
 d. Разделим обе части уравнения (6.3) на
d. Разделим обе части уравнения (6.3) на  . Получим уравнение, равносильное уравнению (6.3),
. Получим уравнение, равносильное уравнению (6.3),
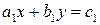 . (6.4)
. (6.4)
По свойству НОД, установленному теоремой 3, числа 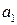 и
и 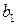 взаимно просты. Тогда составим вспомогательное уравнение
взаимно просты. Тогда составим вспомогательное уравнение
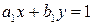 . (6.5)
. (6.5)
Найдем его частное решение 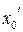 ,
, 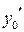 – при помощи алгоритма Евклида, так же, как выше было найдено решение уравнения (6.1).
– при помощи алгоритма Евклида, так же, как выше было найдено решение уравнения (6.1).
Тогда, очевидно, в качестве частного решения уравнения (6.4) можно взять числа 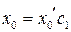 и
и 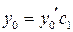 , а общим решением уравнения (6.4) является
, а общим решением уравнения (6.4) является
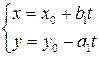 , где
, где 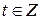 .
.
Пример. Решим уравнение 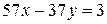 . Поскольку
. Поскольку 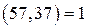 , уравнение имеет решение. Составим вспомогательное уравнение:
, уравнение имеет решение. Составим вспомогательное уравнение:
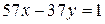 . При помощи алгоритма Евклида представим НОД чисел
. При помощи алгоритма Евклида представим НОД чисел 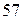 и
и 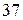 в виде линейной комбинации этих чисел с целыми коэффициентами:
в виде линейной комбинации этих чисел с целыми коэффициентами:
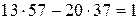 . Таким образом, получим частное решение вспомогательного уравнения:
. Таким образом, получим частное решение вспомогательного уравнения: 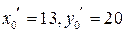 и частное решение исходного уравнения:
и частное решение исходного уравнения: 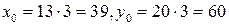 . Тогда общее решение исходного уравнения имеет вид:
. Тогда общее решение исходного уравнения имеет вид: 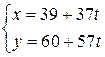 , где
, где 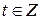 .
.
Дата добавления: 2021-02-19; просмотров: 133;










