Теплоёмкость идеального газа

Основные законы термодинамики были установлены опытным путём. Можно показать, что такие характеристики системы, как теплоёмкость, внутренняя энергия, энтропия и др. могут быть получены методами термодинамики и методами статистической физики.

Число степеней свободы системы i – количество независимых координат, с помощью которых можно полностью описать положение системы в пространстве. Так, для одноатомной молекулы i = 3, т.к. необходимо задать три координаты молекулы, например, координаты x, y, z в декартовой системе. Для двухатомной молекулы i = 3+3-1=5, т.к. число степеней свободы уменьшается на число жёстких связей между атомами, в данном случае на единицу. Если молекула может совершать колебательное и вращательное движения, то число степеней свободы увеличивается: i = n_пост+n_вращ+2n_колеб. Опытным путём в термодинамике было доказано, что на каждую степень свободы приходится энергия 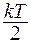. Рассчитываем, например, внутреннюю кинетическую энергию системы из N молекул идеального газа, учитывая, что поступательному движению отдельной молекулы соответствует 3 степени свободы:

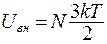(9.24)

Методами статистической физики было доказано, что внутренняя энергия идеального газа равна суммарной средней кинетической энергии движения молекул:

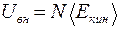(9.25)

Средняя кинетическая энергия молекул:

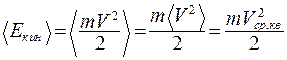(9.26)

где V_ср.кв – среднеквадратичная скорость молекул.

Из распределения Максвелла частиц по скоростям следует, что квадрат среднеквадратичной скорости пропорционален абсолютной температуре:

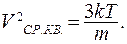(9.27)

Подставим (9.26) и (9.27) в соотношение (9.25) и находим:

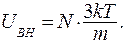(9.28)

Таким образом, термодинамическими и статистическими методами мы пришли к одинаковому результату. В общем случае внутренняя энергия n молей идеального газа:

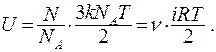(9.29)

где 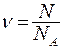- количество молей газа, 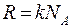- универсальная газовая постоянная.

Применим первое начало термодинамики для получения теплоемкости идеального газа. Пусть имеется 1 моль идеального газа. Теплоемкость, по определению, равна количеству теплоты, необходимому для изменения температуры системы на один Кельвин:

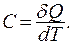(9.30)

Молярной теплоемкостью называется теплоемкость одного моля вещества. Размерность молярной теплоемкости 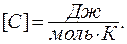Удельной называется теплоемкость единицы массы вещества: 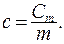Размерность удельной теплоемкости: 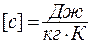. Между удельной и молярной теплоемкостями существует связь 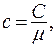где m - молярная масса вещества.

При протекании изохорного процесса ( 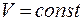) теплоемкость одного моля вещества:

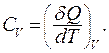
Из первого начала термодинамики следует:

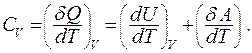
В изохорном процессе газ не совершает работы, 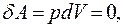отсюда следует:

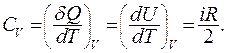(9.31)

Изменение внутренней энергии в изохорном процессе для произвольного количества вещества:

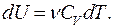(9.32)

При протекании изобарного процесса (P = const), теплоемкость одного моля вещества:

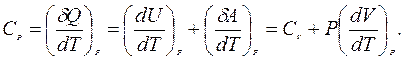(9.33)

Из уравнения Менделеева – Клапейрона для одного моля газа находим:

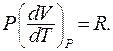(9.34)

Из (9.33) и (9.34) следует, что теплоемкость идеального газа при постоянном давлении:

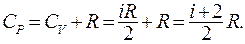(9.35)

Уравнение, связывающие молярные теплоемкости C_P и C_V называется уравнением Роберта – Майера:

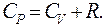(9.36)