Параметрический стабилизатор напряжения.

В схеме выпрямительного устройства, рассмотренного на лекции №2 (рис. 3.1) для преобразования переменного напряжения сети в постоянное напряжение рассмотрены трансформатор, выпрямитель и сглаживающий фильтр. Напряжение на нагрузке поддерживается постоянным по значению с помощью стабилизатора Ст. Простейший стабилизатор напряжения – параметрический, в котором используются специальный диод – СТАБИЛИТРОН.

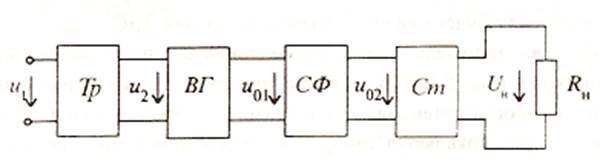
Рис.3.1.

Стабилитрон имеет специфическую вольтамперную характеристику (ВАХ ) в обратном включении (рис.3.2). При отрицательном напряжении ВАХ имеет достаточно протяженный участок, на котором напряжение изменяется мало, а ток изменяется значительно.

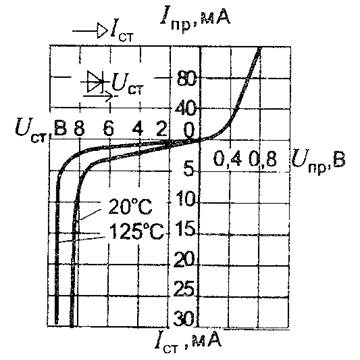
Рис. 3.2. Пример вольтамперной характеристики полупроводникового стабилитрона.

Стабилитрон используется в параметрическом стабилизаторе напряжения (рис.3.3а).

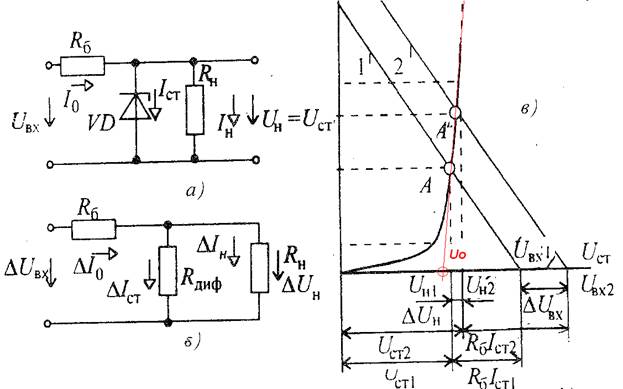
Рис. 3.3. Параметрический стабилизатор напряжения.

а) электрическая схема стабилизатора,

б) линейная схема замещения для малых изменений токов и напряжений (R_диф=ΔU_ст./ ΔI_ст = ΔU_Н/ ΔI_ст –дифференциальное сопротивление)

в) графическое представление состояния стабилитрона и принципа стабилизации напряжения на нагрузке (ΔU_Н<<ΔU_вх) при изменении напряжения U_вх и большом сопротивлении нагрузки (R_Н>> R_диф).

Принцип стабилизации заключается в следующем. Напряжение на стабилитроне, т.е. на нагрузке, остается постоянным из-за изменения тока стабилитрона и вызванного этим изменения напряжения на балластном резисторе.

Схема на рис.3.3а описывается нелинейной системой уравнений:

I₀ - I_ст - I_н = 0 (1)

U_ст( I_ст ) - R_н I_н = 0 (2)

- U_вх + R_бI₀ + R_нI_н = 0 (3)

Преобразуем систему к одному уравнения относительно тока I_ст.

Из (1) имеем I_н = I₀ - I_ст , тогда из (3) следует

- U_вх + R_бI₀ + R_н ( I₀ - I_ст ) = 0 ,

отсюда I₀ =(R_н I_ст + U_вх ) / (R_б + R_н) и из (2) получаем

U_ст(I_ст) = R_н [ (R_н I_ст + U_вх ) / (R_б+R_н) - I_ст]. (4)

Этот же результат можно получить, если применить к схеме на рис.3.3а преобразование по методу эквивалентного активного двухполюсника, в который включим источник входного напряжения U_вх , балластный резистор R_б и приемник R_н (рис. 3.4).

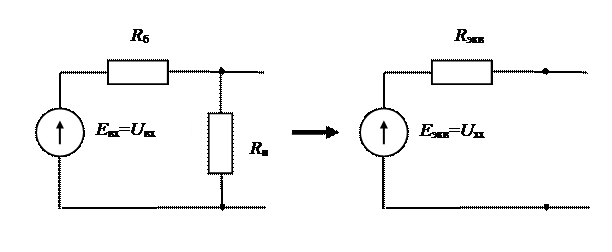
Рис. 3.4. Преобразование части схемы методом эквивалентного активного двухполюсника.

Эквивалентный источник имеет

ЭДС E_экв = U_вх R_н / ( R_н + R_б ) и

сопротивление R_экв = R_б R_н / ( R_н + R_б ).

После эквивалентного преобразования схема рис.3.3а приобретает вид (рис.3.5)

Рис.3.5

Из схемы на рис.3.5 получаем уравнение состояния параметрического стабилизатора:

U_ст ( I_ст ) = E_экв - R_экв I_ст (5)

Если в (5) подставить выражения вместо E_экв и R_экв, то получим уравнение (4). Применение метода эквивалентного источника позволяет лучше представить физически принцип действия стабилизатора, зависимость его свойств от параметров элементов.

Уравнение (4) пригодно для анализа свойств параметрического стабилизатора при любых параметрах элементов.

Положим (наиболее частый случай), что сопротивление нагрузки R_н значительно больше сопротивления балластного резистора R_б. Тогда сопротивление нагрузки можно не учитывать и в схеме виден делитель входного напряжения из балластного резистора R_б и стабилитрона VD (рис.3.3а). Состояние цепи устанавливается в соответствие с рис.3.3в в точке A, где пересекаются ВАХ стабилитрона и прямая линия 1, отсекающая на осях отрезки U_вх1 и U_вх1 /R_б. При увеличении входного напряжения до U_вх2 (линия 2) увеличивается ток стабилитрона (рабочая точка A’), увеличивается напряжение на R_б , а напряжение на нагрузке соответственно увеличивается на ΔU_н. При этом, как видно из графиков ΔU_н << ΔU_вх (R_диф <<R_б).

Для получения простых соотношений для оценки качества параметрического стабилизатора получим линейную его схему замещения с помощью уравнения (5).

Приближенно, если рабочая точка А стабилитрона находится на участке стабилизации, ВАХ стабилитрона на участке стабилизации можно заменить прямой линией с угловым коэффициентом R_диф=ΔU_ст./ ΔI_ст = ΔU_Н/ ΔI_ст:

U_ст( I_ст ) = U₀ + R_диф I_ст

С учетом этой линеаризации уравнение (5) можно переписать :

U₀+ R_дифI_ст =E_экв-R_экв I_ст (6).

Здесь E_экв= R_НU_вх/(R_Н+ R_Б) и R_экв = R_Б R_Н /(R_Б+ R_Н).

Из (6) следует уравнение, если учесть, что R_экв>> R_диф:

I_ст =(E_экв- U₀ )/ (R_экв+ R_диф) =(E_экв- U₀ )/ R_экв (7).

Подставим сюда выражение для E_экв и получим

I_ст =(R_НU_вх/(R_Н+ R_Б) - U₀ )/ R_экв = U_вх /R_Б - U₀ / R_экв

и напряжения на нагрузке принимает вид:

U_н=U_ст(I_ст)=U₀+ R_диф (U_вх /R_Б - U₀ / R_экв) (7)

Отсюда следует, что при изменениях входного напряжения:

ΔU_н=(dU_ст/dU_вх) * Δ U_вх= R_диф/R_б * Δ U_вх (8)

Отношение приращений напряжения на нагрузке и на входе параметрического стабилизатора равно:

ΔU_н /Δ U_вх = R_диф/R_б (8)

Если изменяется сопротивление нагрузки, то

U_н= U₀+ R_диф [U_вх /R_Б - U₀ (R_Б+ R_Н)/ (R_Б R_Н)] (9)

Из уравнения (9) следует, что при изменениях сопротивления нагрузки так же будет достигаться эффект стабилизации напряжения на нагрузке

ΔU_н=(dU_ст/dR_Н) * Δ R_Н= R_диф/ R²_н* U₀ Δ R_Н

.

В практических случаях параметры схемы и стабилитрона подбираются таким образом, чтобы рабочая точка на в.а.х. стабилитрона перемещалась в пределах участка стабилизации (I_ст.мин ,I_{ст.макс}) при необходимом U_ст., которые записаны в паспорте стабилитрона.

С помощью параметрического полупроводникового стабилизатора напряжения можно получить коэффициент стабилизации, который равен отношению относительных изменений входного и выходного напряжений:

K_ст. = (ΔU_вх /U_вх )/ (ΔU_вых /U_вых ) <=100.

Во многих случаях это значение оказывается недостаточным и тогда применяются более сложные «компенсационные стабилизаторы напряжения», содержащие транзисторы.

Заметим так же, что в параметрическом стабилизаторе напряжения нагревание балластного резистора приводит к потерям энергии. Поэтому к.п.д. параметрического стабилизатора напряжения не превышает 30%.

Демонстрация ВАХ реального стабилитрона demo3_1 приведена на рис. 3.6

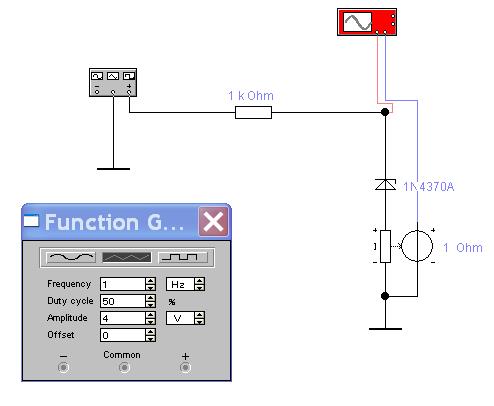
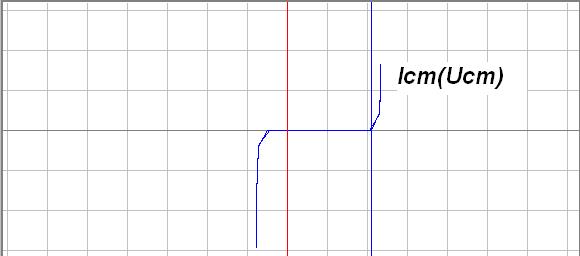
Рис. 3.6. К demo3_1.

Демонстрация работы параметрического стабилизатора напряжения demo3_2 приведена на рис. 3.7.

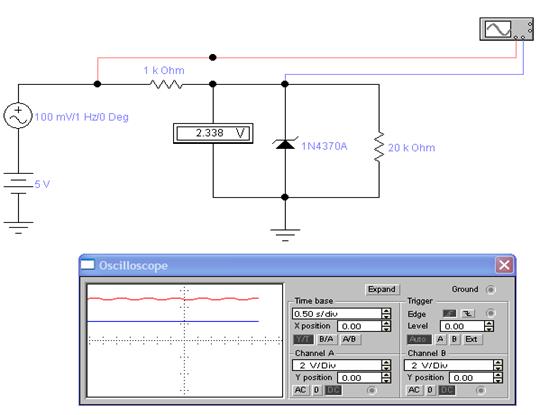
Рис. 3.7.К demo3_2.

Замечание.

Рассмотренный параметрический стабилизатор напряжения позволяет познакомиться с широко применяемым методом описания нелинейных схем с помощью линеаризованных схем замещения. Запишем систему уравнений (1)-(3), заменив в уравнении (2) ВАХ стабилитрона линеаризованным выражением:

I₀-I_ст-I_н =0 (1а)

U₀+R_дифI_ст-R_нI_н=0 (2а)

- U_вх +R_бI₀+R_нI_н=0 (3а)

Для малых изменений токов и напряжений, вызванных изменением входного напряжения, отсюда следует:

ΔI₀-ΔI_ст-ΔI_н =0 (9)

R_дифΔI_ст-R_нΔI_н=0 (10)

-ΔU_вх +R_бΔI₀+R_нΔI_н=0 (11)

Этой системе уравнений соответствует схема замещения, приведенная на рис.3.3 б.