Blum, Blum, and Shub

Простейший и наиболее эффективный генератор, использующий сложностно-теоретический подход, в честь своих авторов называется Blum, Blum, and Shub. Мы сократим его название до BBS, хотя иногда его называют генератором с квадратичным остатком [193].

Теория генератора BBS использует квадратичные остатки по модулю n(см. раздел 11.3). Вот как он работает.

Сначала найдем два простых числа, pи q, которые конгруэнтны 3 modulo 4. Произведение этих чисел, n, является целым числом Блюма (Blum). Выберем другое случайное целое число x, взаимно простое с n. Вычислим

x₀= x²mod n

Это стартовое число генератора.

Теперь можно начать вычислять биты. i-ым псевдослучайным битом является младший значащий бит x_i, где

x_i= x_i-1² mod n

Самым интригующим свойством этого генератора является то, что для получения i-го бита не нужно вычислять предыдущие i-1 биты. Если вам известны pи q, вы можете вычислить i-ый бит непосредственно.

b_i- это младший значащий бит x_i,где x_i =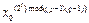

Это свойство означает, что вы можете использовать этот криптографически сильный генератор псевдослучайных чисел в качестве потоковой криптосистемы для файла с произвольным доступом.

Безопасность этой схемы основана на сложности разложения n на множители. Можно опубликовать n, так что кто угодно может генерировать биты с помощью генератора. Однако пока криптоаналитик не сможет разложить n на множители, он никогда не сможет предсказать выход генератора - ни даже утверждать что-нибудь вроде: "Следующий бит с вероятностью 51 процент будет единицей".

Более того, генератор BBS непредсказуем в левом направлении и непредсказуем в правом направлении.Это означает, что получив последовательность, выданную генератором, криптоаналитик не сможет предсказать ни следующий, ни предыдущий бит последовательности. Это вызвано не безопасностью, основанной на каком-то никому не понятном сложном генераторе битов, а математикой разложения n на множители.

Этот алгоритм медленен, но есть способы его ускорить. Оказывается, что в качестве псевдослучайных битов можно использовать несколько каждого x_i. В соответствии с [1569, 1570, 1571, 35, 36] если n- длина x_i, можно использовать log₂n младших значащих битов x_i. Генератор BBS сравнительно медленный и не подходит для потоковых шифров. Однако для высоконадежных приложений, таких как генерация ключей, этот генератор лучше многих других.