Сравнение и измерение
ОСНОВНЫЕ МЕТОДЫ ПРОВЕДЕНИЯ НАУЧНЫХ ИССЛЕДОВАНИЙ
В соответствии с двумя взаимосвязанными уровнями научного познания (эмпирическим и теоретическим) различают эмпирические методы научных исследований (наблюдение, описание, сравнение, измерение, эксперимент, индукция и др.), с помощью которых осуществляется накопление, фиксация, обобщение и систематизация опытных данных, их статистическая обработка, и теоретические (анализ и синтез, аналогия и моделирование, идеализация, дедукция и др.); с их помощью формируются законы науки, теории.
В процессе научного исследования целесообразно использовать многообразные методы, а не ограничиваться каким-то одним.
Наблюдение
Наблюдение – это целенаправленное систематическое восприятие объекта, доставляющее первичный материал для научного исследования. Наблюдение – это метод познания, при котором объект изучают без вмешательства в него. Целенаправленность – важнейшая характеристика наблюдения. Наблюдение характеризуется также систематичностью, которая выражается в восприятии объекта многократно и в разных условиях, планомерностью, исключающий пробелы в наблюдении, и активностью наблюдателя, его способностью к отбору нужной информации, определяемой целью исследования.
Непосредственные наблюдения в истории науки постепенно сменились наблюдениями с помощью все более совершенных приборов – телескопов, микроскопов, фотокамер и т.п. Затем появился еще более опосредованный метод наблюдений. Он позволил не только приближать, увеличивать или запечатлевать изучаемый объект, но и преобразовывать информацию, недоступную нашим органам чувств, в доступную для них форму. В этом случае прибор-посредник играет роль не только "посыльного", но и "переводчика". Так, например, радиолокаторы трансформируют улавливаемые радиолучи в световые импульсы, которые могут видеть и наши глаза.
Как метод научного исследования наблюдение дает исходную информацию об объекте, необходимую для его дальнейшего исследования.
Сравнение и измерение
Важную роль в научных исследованиях играют сравнение и измерение. Сравнение представляет собой метод сопоставления объектов с целью выявления сходства или различия между ними. Сравнение – это операция мышления, посредством которой классифицируется, упорядочивается и оценивается содержание действительности. При сравнении производят попарное сопоставление объектов в целях выявления их отношений, сходственных или отличительных признаков. Сравнение имеет смысл только применительно к совокупности однородных предметов, образующих класс.
Измерение – это нахождение физической величины опытным путем с помощью специальных технических средств.
Целью измерения является получение информации об исследуемом объекте.
Измерение может проводиться в следующих случаях:
– в чисто познавательных задачах, в которых осуществляется всестороннее изучение объекта, без четкого сформулированных идей по применению получаемых результатов в прикладной деятельности;
– в прикладных задачах, связанных с выявлением определенных свойств объекта, существенных для вполне конкретного применения.
Теорией и практикой измерения занимается метрология – наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности.
Для точных наук характерна органическая связь наблюдений и экспериментов с нахождением числовых значений характеристик исследуемых объектов. По образному выражению Д. И. Менделеева, «наука начинается с тех пор, как начинают измерять.
Любое измерение может быть осуществлено в том случае, если имеются следующие элементы: объект измерения, свойство или состояние которого характеризует измеряемая величина; единица измерения; способ измерения; технические средства измерения, проградуированные в выбранных единицах; наблюдатель или регистрирующее устройство, воспринимающее результат.
Различают прямое и косвенное измерения. При первом из них результат получают непосредственно из измерения (например, измерение длины линейкой, массы с помощью гирь). Косвенные измерения базируются на использовании известной зависимости между искомым значением величины и значениями непосредственно измеряемых величин.
К средствам измерений относят измерительный инструмент, измерительные приборы и установки. Измерительные средства делят на образцовые и технические.
Образцовые средства являются эталонами. Они предназначены для проверки для проверки технических, т. е. рабочих средств.
Передача размеров единиц от эталонов или образцовых средств измерений рабочим средствам осуществляется государственными и ведомственными метрологическими органами, составляющими отечественную метрологическую службу, их деятельность обеспечивает единство измерений и единообразие средств измерений в стране. Основоположником метрологической службы и метрологии как науки в России был великий русский ученый Д. И. Менделеев, создавший в 1893 г. Главную Палату мер и весов, которой проведена, в частности, большая работа по внедрению метрической системы в стране (1918 – 1927).
Одной из важнейших задач при проведении измерений является установление их точности, т е. определение погрешностей (ошибок). Погрешностью или ошибкой измерения называют отклонение результата измерения физической величины от ее истинного значения.
Если погрешность мала, то ею можно пренебречь. Однако при этом неизбежно возникают два вопроса: во-первых, что понимать под малой погрешностью, и, во-вторых, как оценить величину погрешности.
Ошибка измерения обычно неизвестна, как неизвестно и истинное значение измеряемой величины (исключения составляют измерения известных величин, проведенные со специальной целью исследования ошибок измерения, например для определения точности измерительных приборов). Поэтому одной из основных задач математической обработки результатов эксперимента как раз и является оценка истинного значения измеряемой величины по получаемым результатам.
Рассмотрим классификацию погрешностей измерения.
Различают систематическую и случайную погрешности измерения.
Систематическая погрешность остается постоянной (или закономерно изменяющейся) при повторных измерениях одной и той же величины. К постоянно действующим причинам этой погрешности относятся следующие: недоброкачественные материалы, комплектующие изделия, применяемые для изготовления приборов; неудовлетворительная эксплуатации, неточная градуировка датчика, применение измерительных приборов невысокого класса точности, отклонение теплового режима установки от расчетного (обычно стационарного), нарушение допущений, при которых справедливы расчетные уравнения и т. п. Такие ошибки легко устраняются при отладке измерительной аппаратуры или введением специальных поправок к значению измеряемой величины.
Случайная погрешность изменяется случайным образом при повторных измерениях и обусловлена хаотическим действием множества слабых, и поэтому трудно выявляемых причин. Примером одной из этих причин является считывание показаний со шкалы стрелочного прибора – результат непредсказуемым образом зависит от угла зрения оператора. Оценить случайную погрешность измерения можно лишь методами теории вероятности и математической статистики. Если погрешность в эксперименте существенно превышает ожидаемую, то ее называют грубой ошибкой (промахом), результат измерения в этом случае отбрасывается. Грубые ошибки возникают вследствие нарушения основных условий измерения или в результате недосмотра экспериментатора (например, при плохом освещении вместо 3 записывают 8). При обнаружении грубой ошибки результат измерения следует сразу отбросить, а само измерение повторить (если это возможно). Внешним признаком результата, содержащего грубую ошибку, является его резкое отличие по величине от результатов остальных измерений.
Другой классификацией погрешностей является их разделение на методические и инструментальные погрешности. Методические погрешности обусловлены теоретическими ошибками выбранного метода измерений: отклонением теплового режима установки от расчетного (стационарного), нарушением условий, при которых справедливы расчетные уравнения и т.п. Инструментальные погрешности вызваны неточной градуировкой датчиков, погрешностями измерительных приборов и т.д. Если методические погрешности в тщательно поставленном опыте можно свести к нулю или учесть введением поправок, то инструментальные погрешности устранить в принципе невозможно – замена одного прибора другим, такого же типа, изменяет результат измерений.
Таким образом, наиболее трудно устраняемыми в эксперименте погрешностями являются случайные и систематические инструментальные погрешности.
Если измерения провести многократно в одних и тех же условиях, то результаты отдельных измерений одинаково надежны. Такую совокупность измерений x1, x2 ...xn называют равноточными измерениями.
При многократных (равноточных) измерениях одной и той же величины x случайные погрешности приводят к разбросу получаемых значений xi, которые группируются вблизи истинного значения измеряемой величины Если проанализировать достаточно большую серию равноточных измерений и соответствующих случайных ошибок измерений, то можно выделить четыре свойства случайных ошибок:
1) число положительных ошибок почти равно числу отрицательных;
2) мелкие ошибки встречаются чаще, чем крупные;
3) величина наиболее крупных ошибок не превосходит некоторого определенного предела, зависящего от точности измерения;
4) частное от деления алгебраической суммы всех случайных ошибок на их общее количество близко к нулю, т.е.
На основе перечисленных свойств при учете некоторых допущений математически достаточно строго выводится закон распределения случайных ошибок, описываемый следующей функцией:
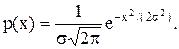
Закон распределения случайных ошибок является основным в математической теории погрешностей. Иначе его называют нормальным законом распределения измеряемых данных (распределением Гаусса). Этот закон в виде графика изображен на рис. 2
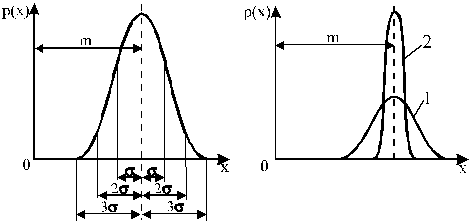
а) б)
Рис. 2. Характеристики нормального закона распределения
р(x) – плотность вероятности получения отдельных значений xi (сама вероятность изображается площадью под кривой);
m – математическое ожидание, наиболее вероятное значение измеряемой величины x (соответствующее максимуму графика), стремящееся при бесконечно большом числе измерений к неизвестному истинному значению x; 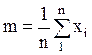 , где n – число измерений. Таким образом, математическое ожидание m определяется как среднее арифметическое от всех значений xi,
, где n – число измерений. Таким образом, математическое ожидание m определяется как среднее арифметическое от всех значений xi,
s – среднее квадратическое отклонение измеряемой величины x от значения m; 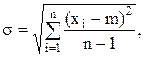 (xi - m) – абсолютное отклонение xi от m,
(xi - m) – абсолютное отклонение xi от m,
Площадь под кривой графика в каком-либо интервале значений x представляет собой вероятность получения случайного результата измерения в этом интервале. Для нормального распределения в интервал ±s (относительно m) попадают 0,62 всех проведенных измерений; в более широком интервале ±2s содержатся уже 0,95 всех измерений, а в интервал ±3s укладываются практически все результаты измерений (кроме грубых ошибок).
Среднее квадратическое отклонение s характеризует ширину нормального распределения. Если повысить точность измерения, разброс результатов резко уменьшится за счет уменьшения s (распределение 2 на рис. 4.3 б уже и острее, чем кривая 1).
Конечной целью эксперимента является определение истинной величины x, к которой при наличии случайных погрешностей можно лишь приблизиться, вычисляя математическое ожидание m для все большего числа экспериментов.
Разброс значений математического ожидания m, вычисленных для различного числа измерений n характеризуется величиной sm; 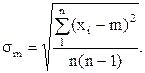 При сравнении с формулой для s видно, что разброс величины m, как средней арифметической, в Ön меньше разброса отдельных измерений xi. Приведенные выражения для sm и s отражают закон возрастания точности при росте числа измерений. Из него следует, что для повышения точности измерений в 2 раза необходимо сделать вместо одного - четыре измерения; чтобы повысить точность в 3 раза, нужно увеличить число измерений в 9 раз и т.д.
При сравнении с формулой для s видно, что разброс величины m, как средней арифметической, в Ön меньше разброса отдельных измерений xi. Приведенные выражения для sm и s отражают закон возрастания точности при росте числа измерений. Из него следует, что для повышения точности измерений в 2 раза необходимо сделать вместо одного - четыре измерения; чтобы повысить точность в 3 раза, нужно увеличить число измерений в 9 раз и т.д.
Для ограниченного числа измерений значение m все же отличается от истинного значения величины x, поэтому наряду с вычислением m необходимо указать доверительный интервал, в котором с заданной вероятностью находится истинное значение x. Для технических измерений вероятность 0,95 считают достаточной, поэтому доверительный интервал при нормальном распределении составляет ±2sm. Нормальное распределение справедливо для количества измерений n ³ 30.
В реальных условиях технический эксперимент редко проводится более 5 – 7 раз, поэтому недостаток статистической информации должен компенсироваться расширением доверительного интервала. В этом случае при (n < 30) доверительный интервал определяется как ± kssm, где ks – коэффициент Стьюдента, определяемый по справочным таблицам
С уменьшением числа измерений n коэффициент ks увеличивается, что расширяет доверительный интервал, а при увеличении n значение ks стремится к 2, что соответствует доверительному интервалу нормального распределения ± 2sm.
Конечный результат многократных измерений постоянной величины всегдаприводится к виду: m ± kssm .
Таким образом, для оценки случайных погрешностей необходимо выполнить следующие операции:
1). Записать результаты x1, x2 ...xn многократных измерений n постоянной величины;
2). Вычислить среднее значение из n измерений – математическое ожидание 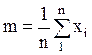 ;
;
3). Определить погрешности отдельных измерений хi -m;
4). Вычислить квадраты погрешностей отдельных измерений (хi -m)2;
если несколько измерений резко отличаются по своим значениям от остальных измерений, то следует проверить не являются ли они промахом (грубой ошибкой). При исключении одного или нескольких измерений п.п. 1...4 повторить;
5). Определяется величина sm – разброс значений математического ожидания m;
6). Для выбранной вероятности (обычно 0,95) и числа проведенных измерений n определяется по справочной таблице коэффициент Стьюдента ks;
Значения коэффициента Стьюдента ks в зависимости от числа измерений n для доверительной вероятности 0,95
| n | ¥ | |||||||
| ks | 12,7 | 3,18 | 2,78 | 2,57 | 2,45 | 2,26 | 2,09 | 2,00 |
7). Определяются границы доверительного интервала ± kssm
8). Записывается окончательный результат m ± kssm.
Инструментальные погрешности устранить в принципе невозможно. Все средства измерения основаны на определенном методе измерения, точность которого конечна.
Инструментальные погрешности устранить в принципе невозможно. Все средства измерения основаны на определенном методе измерения, точность которого конечна. Погрешность прибора определяется точностью деления шкалы прибора. Так, например, если шкала линейки нанесена через 1 мм, то точность отсчета (половина цены деления 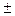 0,5 мм) не изменить, если применить лупу для рассматривания шкалы.
0,5 мм) не изменить, если применить лупу для рассматривания шкалы.
Различают абсолютную и относительную погрешности измерения.
Абсолютная погрешность D измеряемой величины x равна разности измеренного и истинного значений:
D = x - xист.
Относительная погрешность e измеряется в долях от найденной величины x:
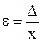 .
.
Для простейших средств измерения – измерительных инструментов абсолютная погрешность измерения D равна половине цены деления. Относительная погрешность определяется по формуле.
| <== предыдущая лекция | | | следующая лекция ==> |
| Препараты по специфической активности | | | ФАКТОРЫ, ОПРЕДЕЛЯЮЩИЕ БЕЗОПАСНОСТЬ ПРОХОДЧЕСКИХ РАБОТ |
Дата добавления: 2016-10-26; просмотров: 5115;










