Непрерывность функции
Функции одной независимой переменной. Пределы. Непрерывность функций. Производная, геометрический смысл. Исследование функций.
Предел функции.
Пусть функция y=f(x) определена в некоторой окрестности точки x0, кроме, быть может, самой точки x0.
О (на « языке последовательностей», или по Гейне):Число А называется пределом функции y=f(x) в точке x0, если для любой последовательности допустимых значений аргумента xn, nÎN (xn¹x0), сходящейся к x0 ( т.е. 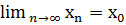 ), последовательность соответствующих значений f(xn),nÎN, сходитьсяк числу А.
), последовательность соответствующих значений f(xn),nÎN, сходитьсяк числу А.
Техника вычисления пределов.
При вычисление предела элементарной функции f(x) приходиться сталкиваться с двумя различными типами примеров.
1. Функция f(x) определена в предельной точке х = а. Тогда 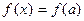
2. Функция f(x) в предельной точке х = а не определена или же вычисляется предел функции при х ® ¥ . Тогда вычисление предела требует в каждом случае индивидуального подхода. В одних случаях ( наиболее простых) вопрос сводиться непосредственно к применению теорем о свойствах бесконечно больших и бесконечно малых функций и связи между ними.
Более сложными случаями нахождения предела являются такие, когда функция f(x) в точке х = а или при х ® ¥ представляет собой неопределенность ( типа 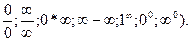
Приведем основные теоремы, на которых основано вычисление пределов.
1) Если существуют 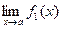 и
и 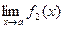 , то
, то
· 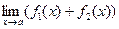 =
= 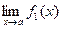 +
+ 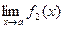
· 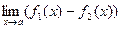 =
= 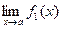 -
- 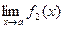
· 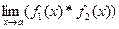 =
= 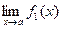 *
* 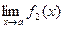
· 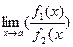 =
= 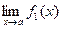 /
/ 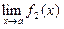 при
при 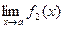 ¹ 0
¹ 0
2) 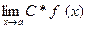 = С*
= С* 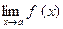 , где С – некоторое число
, где С – некоторое число
3) Связь между бесконечно малой и бесконечно большой величинами (С– некоторое число): 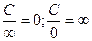
Рассмотрим некоторые ПРИМЕРЫ:
Пример 1. Найти предел функции 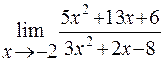
Решение: Имеем неопределенность вида 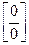 . Для ее раскрытия разложим числитель и знаменатель на множители и сократим на общий множитель
. Для ее раскрытия разложим числитель и знаменатель на множители и сократим на общий множитель 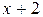 , который при
, который при 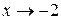 не равен нулю. В результате неопределенность будет раскрыта.
не равен нулю. В результате неопределенность будет раскрыта.
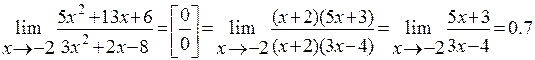
Пример 2. Найти предел функции 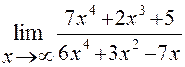
Решение: Имеем неопределенность вида 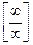 . Для ее раскрытия можно либо разделить числитель и знаменатель на наибольшую степень переменной x и учитывая, что величина обратная бесконечно большой величине есть бесконечно малая величина, раскроем исходную неопределенность, либо вынести переменную в наибольшей степени в числители и знаменатели дроби и сократить на наибольшую степень.
. Для ее раскрытия можно либо разделить числитель и знаменатель на наибольшую степень переменной x и учитывая, что величина обратная бесконечно большой величине есть бесконечно малая величина, раскроем исходную неопределенность, либо вынести переменную в наибольшей степени в числители и знаменатели дроби и сократить на наибольшую степень.
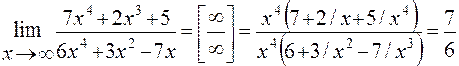
Пример 3. Найти предел функции 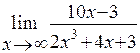
Решение: Имеем неопределенность вида 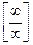 . Раскрываем ее аналогично тому как это сделано в примере 2.
. Раскрываем ее аналогично тому как это сделано в примере 2.
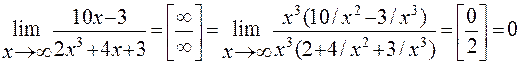
Пример 4. Найти предел функции 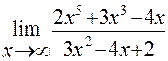
Решение: Имеем неопределенность вида 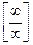 . Раскрываем ее аналогично тому как это сделано в примере 2.
. Раскрываем ее аналогично тому как это сделано в примере 2.
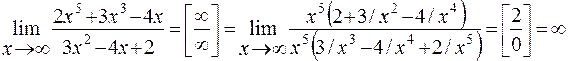
Пример 5. Найти предел функции 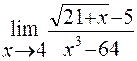
Решение: Имеем неопределенность вида 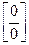 . Для ее раскрытия умножим числитель и знаменатель на выражение сопряженное числителю, разложим выражение стоящее в знаменателе на множители по формуле разности кубов и сократим числитель и знаменатель на общий множитель
. Для ее раскрытия умножим числитель и знаменатель на выражение сопряженное числителю, разложим выражение стоящее в знаменателе на множители по формуле разности кубов и сократим числитель и знаменатель на общий множитель 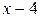 , который при
, который при 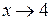 не равен нулю. В результате неопределенность будет раскрыта.
не равен нулю. В результате неопределенность будет раскрыта.
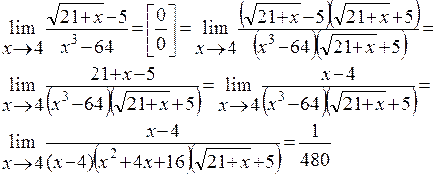
Вычисление пределов с использованием замечательных пределов.
Применение замечательных пределов
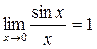 и
и 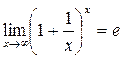
Пользуясь этими формулами, можно вычислить ряд пределов.
Пример 6. Вычислить 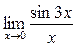 .
.
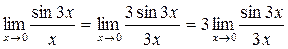 , заменяя 3x = y и учитывая, что y → 0 при x → 0, получаем:
, заменяя 3x = y и учитывая, что y → 0 при x → 0, получаем:
 .
.
Пример 7 . Вычислить 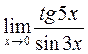
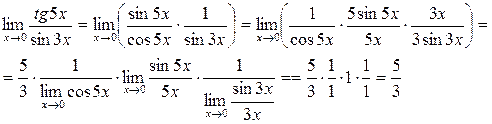
Здесь мы воспользовались известным из курса средней школы пределом:
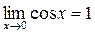 .
.
Пример 8 . Вычислить 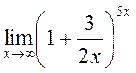
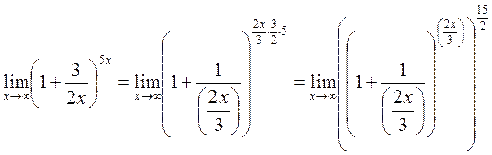
Заменяя 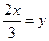 и учитывая, что y → ∞ при x → ∞, можем написать:
и учитывая, что y → ∞ при x → ∞, можем написать:
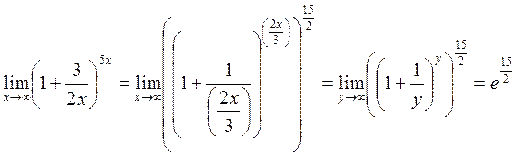 .
.
Непрерывность функции
О: Функция y = f(x) называется непрерывной в точке х = а, если существует предел функции в этой точке, который равен значению функции в этой точке, т.е. 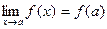 .
.
Примером непрерывной функции может служить любая элементарная функция, которая непрерывна в каждой точке своей области определения.
Точка х = а называется точкой разрыва функции y=f(x), если эта функция определена в некоторой окрестности точки х = а, но в самой точке х = а не удовлетворяет условию непрерывности.
Точки разрыва функции делятся на два типа. К точкам разрыва I рода относятся такие точки, в которых существуют конечные односторонние пределы: 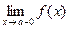 (левый предел) и
(левый предел) и 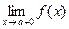 (правый предел). К точкам разрыва II рода относятся те точки, в которых хотя бы один из односторонних пределов не существует или бесконечен.
(правый предел). К точкам разрыва II рода относятся те точки, в которых хотя бы один из односторонних пределов не существует или бесконечен.
Задание 4. Исследовать данную функцию на непрерывность и построить ее график
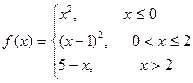
Решение:Функция 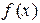 является неэлементарной, так как на разных интервалах представлена различными аналитическими выражениями. Эта функция определена на интервалах (-∞;0), (0;2) и (2; +∞), где она задана непрерывными элементарными функциями. Внутри каждого интервала указанные элементарные функции не имеют точек разрыва, следовательно, разрыв возможен только в точках перехода от одного аналитического выражения к другому, т.е. в точках х1 = 0 и х2 = 2.
является неэлементарной, так как на разных интервалах представлена различными аналитическими выражениями. Эта функция определена на интервалах (-∞;0), (0;2) и (2; +∞), где она задана непрерывными элементарными функциями. Внутри каждого интервала указанные элементарные функции не имеют точек разрыва, следовательно, разрыв возможен только в точках перехода от одного аналитического выражения к другому, т.е. в точках х1 = 0 и х2 = 2.
Для точки х1 = 0 имеем:
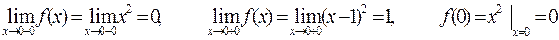
Так как 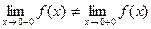 , то функция
, то функция 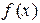 в точке х1 = 0 имеет разрыв первого рода.
в точке х1 = 0 имеет разрыв первого рода.
Для точки х2 = 2 находим:
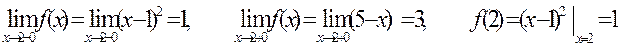
Так как 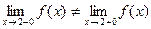 , то функция
, то функция 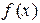 в точке х2 = 2 имеет разрыв первого рода.
в точке х2 = 2 имеет разрыв первого рода.
График данной функции изображен на рис. 1.
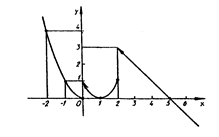
Рис. 1.
3.3 Производная, геометрический смысл.
Основные правила дифференцирования
а) c’ = 0; б) (и ± υ)’ = и’ ± υ’; в) (иυ)’ = и’υ + иυ’; г ) 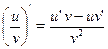
д) дифференцирование сложной функции, если 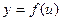 ,
, 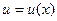 то
то 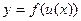 - сложной функция. Тогда,
- сложной функция. Тогда, 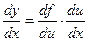 или
или 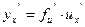
Здесь c = const, а и и υ - дифференцируемые функции.
Таблица производных основных элементарных функций
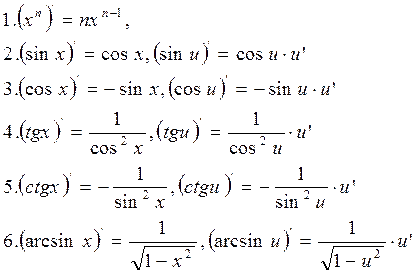
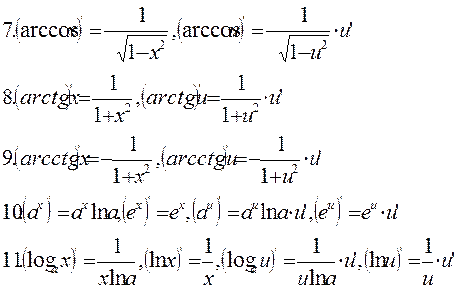
Пример: Найти производные следующих функций :
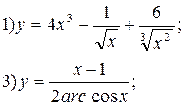
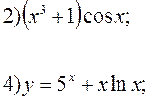
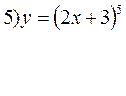
Решение. 1) Запишем данную функцию следующим образом:
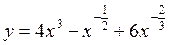 .
.
Тогда
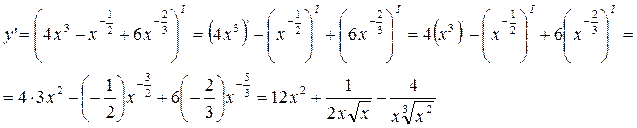
2) Имеем
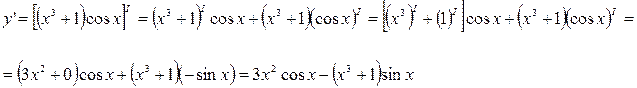
3) Имеем
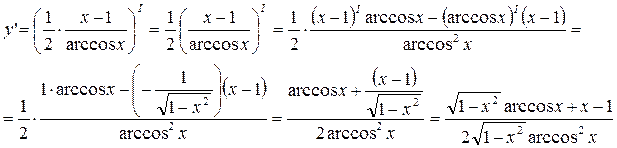
4) Имеем
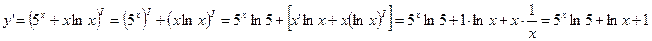
5) Имеем
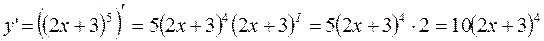 ;
;
Геометрическое приложение производной.
Производная функции y = y (x) при данном значении аргумента x = x0 равна угловому коэффициенту касательной, проведённой к графику этой функции в точке с абсциссой x0. (См. рис.):
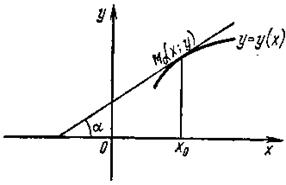 y'(x0)=tgα. (1)
y'(x0)=tgα. (1)
Уравнение прямой к графику функции
y = y (x) в точке М0 (x0 ; y0) имеет вид
y - y0 = y’(x0) (x - x0) . (2)
Если y (x) имеет при x = x0 бесконечную производную, то уравнение касательной таково:
x = x0. (3)
Уравнение нормали, т.е. прямой, проходящей через точку касания М0 (x0 ; y0) перпендикулярно касательной, записывается в виде
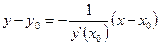 (4)
(4)
Пример: Составить уравнение касательной и нормали к параболе y = 2x2 - 6x + 3 в точке М0 (1 ; -1).
Решение. Найдём производную функции y = 2x2 - 6x + 3 при x = 1. Имеем y’ = 4x - 6, откуда y’ (1) = -2.
Воспользовавшись уравнением (2), получим искомое уравнение касательной :
y - (-1) = -2 (x - 1), или 2x + y - 1 = 0.
Уравнение нормали получим, используя уравнение (4) :
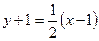 , или x - 2y - 3 = 0.
, или x - 2y - 3 = 0.
| <== предыдущая лекция | | | следующая лекция ==> |
| Подготовка, оформление и ведение графических документов, используемых сотрудниками органов внутренних дел в особых условиях | | |
Дата добавления: 2021-01-26; просмотров: 200;










