Колориметрия негіздері

Жұлдыздар сәулеленуі туралы информация – бұл олардың спектрлеріндегі энергия таралуы, ол абсолюттік энергетикалық бірліктерде сипатталады. Жұлдыздар спектріндегі энергия таралуы туралы мәліметті олардың спектрінің әртүрлі бөліктеріндегі сәуле шығаруын өлшеу арқылы алуға болады, ол үшін жарық сүзгісі (светофильтр) қолданады. Визуалды фотометрлерді пайдаланып алынған жұлдыздық шамалар визуалды деп аталады. Бұл әдіс фотографияға пайда болғанға дейін қолданылады. Қазіргі кезде ол аз қолданылады.

Жұлдыздар кескінінің фотометрлік өлшеу әдісі арқылы алынатын жұлдыздық шамалар фотографиялық деп аталады. Жұлдыздан келетін сәулелер ағынын дәл анықтау фотоэлектрлік фотографиялық әдістер арқылы жүзеге асады. Ол үшін арнайы іріктеліп алып ( светофильтрлері – жарық сүзгілері) пайдаланады. Олар халықаралық жүйеде U,B,V деп белгіленеді, яғни бұл спектрдің 3 бөлігі – ультракүлгін (U), көк (B) және сары (V- визуалды). Басқа да көп түсті фотометрлік жүйелер бар.

Берілген жүйедегі жұлдыздық шамаларды анықтау үшін зерттелетін жұлдыздан келетін жарық ағындары мен стандарт ретінде қабылдаған салыстыру жұлдыздарының жарық ағындарын салыстырады.

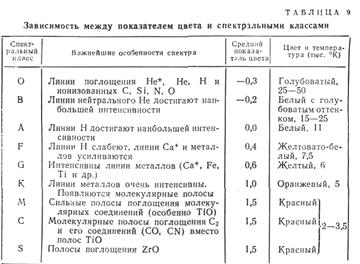
Төмендегі кестеге әртүрлі спектрлік кластарға жататын жұлдыздық түс көрсеткіштерінің мәндері келтірілген. Жұлдыздың түс көрсеткіштерін зерттеуге арналған астрофизика бөлімі – колориметрия деп аталады. Оның мақсаты түс көрсеткіштерін әртүрлі әдістермен өлшеу, жұлдыздар сәуле шығаруының спектрлік құрамын сипаттайтын басқа да шамаларды табу.

9 -кесте.

3.4.4. Спектр – жарықтылық (Герцшпрунг-Рассел) диаграммасы

XX ғасыр басында Дат астрономы Герцшпрунг және одан кейінірек американ астрофизигі Рассел жұлдыздардың спектрі мен жарықтылығы арасындағы байланысты анықтады. Бұл тәуелділік график ретінде келтірілді. Бір оське спектрлік класс, ал екіншісіне абсолют жұлдыздық шама сызылады. Бұл график спектр-жарықтылық немесе Герцшпрунг-Рассел диаграммасы деп аталады (3.12 сурет). Абсолют жұлдыздық шама орнына жарықтылықты (әдетте log шкалада), ал спектрлік кластар орнына – түстердің көрсеткіші - әсерлі (эффективті) температураның өзін келтіруге болады.

Әрбір жұлдыздың орны оның физикалық табиғаты және даму кезеңімен анықталады. Герцшпрунг-Рассел диаграмасында жұлдыздар жүйесінің бүкіл тарихы келтіріледі. Бұл диаграмма физикалық қасиеттері ортақ жұлдыздар тобын және олардың кейбір физикалық сипаттамалары арасындағы тәуелділікті анықтауға мүмкіндік береді. (мысалы: химиялық құрамы, эволюциясы,...т.с.с.).

Диаграмманың жоғарғы бөлігі жарықтылығы жоғары жұлдыздарға сәйкес келеді, ал төменгі бөлігін жарықтылығы төмен жұлдыздар қамтыған. Диаграмманың сол жағында ертеректегі ыстық жұлдыздар орналасқан, ал оң жағында кейінгі спектрлік кластағы суық жұлдыздар орналасқан.

Диаграмманың жоғарғы жағында жарықтылығы жоғары (алыптар және аса алыптар) орналасқан. Диаграмманың төменгі бөлігіндегі жұлдыздардың жарықтылығы төмен топтары орналасқан және олар ергежейлілер деп аталады. Жоғарғы бөліктегі жұлдыздар жиі орналасқан және солдан оңға қарай бағытталған диагональ – бас тізбек деп аталады. Бұл тізбектің маңайында ыстық (жоғарғы жағы) және суық (төменгі бөлігі) жұлдыздар орналасқан.

Жалпы алғанда, Герцшпрунг-Рассел диаграммасындағы жұлдыздар белгілі ретпен орналасқан, ал бұл жарықтық пен температура арасында қандай да бір тәуелділік бар деген сөз. Бірақ диаграмманы мұқият қарасақ, онда басқа да қосымша тізбектер бар екенін көруге болады. Бұл тізбектер белгілі бір жұлдыздар топтарының жарықтылығымен температурасы арасында жекелеген тәуелділіктер бар екенін білдіреді.

Қарастырылған тізбектер жарықтық кластары деп аталады және олар спектрлік кластардан кейін қойылатын Ι ÷ ΙΙ дейінгі рим сандары арқылы белгілейді. Сонда, жұлдыздардың толық классификациясы 2 параметрге тәуелді болады, біріншісі - спектрді, екіншісі – жарықтылықты сипаттайды. Мысалы, Күн бас тізбекте жатыр, ол V жарықтылық класына жатады және оның спектрінің белгіленуі - G2V. Қазіргі кезде қабылданған осы классификация МК (Морган, Кинан) классификациясы деп аталады.

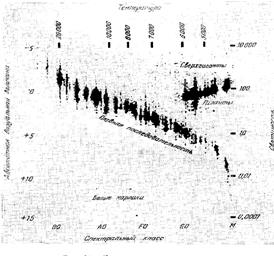
Сурет 3.12 Спектр-жарықтылық диаграммасы

Жарықтылық кластары 3.13 – суретте көрсетілген.

Ι жарықтылық класы – аса алыптар (сверх гиганты) - бұл жұлдыздар спектр - жарықтылық диаграммасының жоғарғы бөлігінде орналасқан және бірнеше тізбектерге бөлінеді.

ΙΙ жарықтылық класы – жарық алыптар;

ΙΙΙ – алыптар;

ΙV – субалыптар. Соңғы үш класс жұлдыздары диаграммада аса алыптар мен бас тізбек аралығындағы облыста орналасқан;

V – бас тізбектің жұлдыздары;

VΙ – жарық субалыптар - олар бас тізбектен бір жұлдыздық шамаға төмен өтетін тізбекті құрайды;

VΙΙ – ақ ергежейлілер - олардың жарықтылығы төмен және диаграмманың төменгі бөлігінде орналасқан.

Жұлдыздардың берілген класқа жату–жатпауы спектрлік классификацияның арнайы қосымша белгілері арқылы анықталады. Мысалы, аса алыптардың спектрлік сызықтары әдетте жіңішке әрі терең болып келеді, ал ақ ергежейлілерде бұған керісінше болып келеді. Өздерінің спектрлері бойынша ақ ергежейлілердің айырмашылығы, олардың кейбір металдарының спектрлік сызықтары алыптарға қарағанда әлсіз.

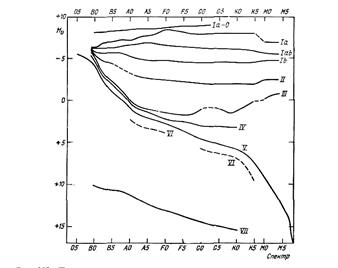
Сурет 3.13 Жарықтылық кластары

Спектрлерлік классификациясының жоғарыда аталған қосымша белгі-шарттары (критерийлері) жарықтылық класын анықтауға және абсолют жұлдыздық шаманы спектроскоптық әдіспен анықтауға негіз болып табылады.

3.4.5. Жұлдыздар өлшемдерін анықтау әдістері

Жұлдыздар радиустарын анықтау мүмкін емес, (кейбір жағдайлардан басқа) себебі олар бізден өте алыс орналасқан және бұрыштық өлшемдері ірі телескоптардың ажырату қабілетінен аз. Егер жақын орналасқан жұлдыздң бұрыштық бұрыштық диаметрі d қандай да бір әдіс көмегімен табылған болса, оның сызықтық өзекшесі D мына өрнек арқылы анықталады:

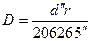(3.4.1)

Жұлдыздық өлшемді жанама әдіс арқылы табуға болады, егер оның болометрлік жарықтығы және әсерлі температураның анықтамасына сәйкес жұлдыздардың 1см² ауданы барлық бағыттар бойынша мынадай энергия ағынын шығарады:

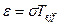(3.4.2)

Егер осы шаманы жұлдыз бетінің ауданына (4πR²)-қа көбейтсек, онда жұлдыз шығаратын толық энергия ағынын толық аламыз. Олай болса жұлдыздың жарықтылығы былайша анықталады:

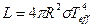(3.4.3)

Алынған өрнекті жарықтылығы мен радиусы белгілі болып табылатын Күнге пайдаланатын болсақ, онда Күннің әсерлі температурасын T _ деп белгілеп, келесі өрнекті аламыз:

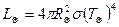(3.4.4)

Жоғарыдағы өрнектерді бір–біріне мүшелеп бөлсек, онда:

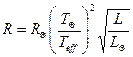(3.4.5)

немесе логарифмдасақ:

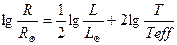(3.4.6)

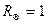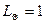Әдетте жұлдыздың радиусы мен жарықтылығын күн бірліктері арқылы өрнектейді және . Олай болса:

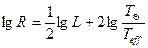(3.4.7)

3.4.6. Радиус-жарықтылық-масса тәуелділігі

Жоғарыда алынған өрнектер маңызды 3 параметрді: радиус, жарықтылық және әсерлі (эффективті) температураны байланыстырады. Сонымен қатар, спектр (яғни, температура) және жарықтылық арасындағы тәуелділік (Герцшпрунг-Рэссел диаграммасы) бізге белгілі. Олай болса, (3.4.7) өрнекке кіретін барлық шамалар өзара тәуелді және жұлдыздардың әрбір тізбегі үшін спектр-жарықтылық диаграммасында спектрлік класс пен радиус арасында белгілі бір заңдылықты табуға болады. Ол үшін спектр-жарықтылық диаграммасының түрін аздап өзгерту керек болады. Визуалды абсолют жұлдыздық шама орнына абсолют болометрлік жұлдыздық шаманы, ал спектрлік класс орнына – сәйкес әсерлі температураны енгіземіз. Бұл жағдайда «ескі» диаграмманың жалпы сипаты негізінен сақталады. Соңғы сызылған диаграммада радиустары бірдей жұлдыздардың орны түзу сызықпен көрсетіледі, себебі Lg L және Lg Т_эфф арасындағы тәуелділік – сызықты. 3.14-суретте тұрақты радиустарының сызықтары келтірілсе, бұл сызықтар бізге жұлдыздардың өлшемдерін олардың жарықтылығы (абсолют жұлдыздық шама) және спектрі (әсерлі температура) бойынша табуға болады. 197-суреттен жұлдыздардың радиустары өте үлкен аралықтарда өзгеретінін көреміз, яғни жүздеген (мыңдаған) 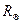- ден (алыптар және аса-алыптар) (10² - 10³) 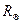-ге (ақ ергежейлілер) дейін. Олай болса, жұлдыздық атмосфералардың температураларының (ерекшеліктері) айырмашылықтарды 10 есеге дейін ғана болса, ал диаметрлеріндегі өзгешелік 10⁶ дәрежесіне дейін жетеді.

3.14–суретте аса алыптардың тізбегі түзу сызықпен келтірілген. Бұл осы жұлдыздар үшін болометрлік жарықтылық пен радиус арасындағы эмпирикалық тәуелділікті анықтауға мүмкіндік береді. Мысалы, бас тізбектегі көптеген жұлдыздар үшін келесі өрнек пайдаланылады:

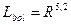
Ал, маңызды шамалардың бірі – массаны дара жұлдыздар үшін анықтау өте қиын. Кейбір жағдайларда Кеплер заңы көмегімен қосжүйелердің компоненттерінің массаларын анықтауға болады. Сондықтан аздаған жұлдыздар тобы үшін массаны болометрлік масса мен болометрлік жарықтылық арасындағы байланыссыз табуға болады, ол 3.15–суретте келтірілген. Бұл суреттегі түзу 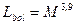тәуелділігін көрсетеді, ол бас тізбектегі көптеген қосжүйелердің компоненттері үшін орындалады.

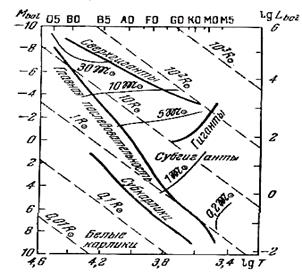
Сурет 3.14 Абсолют жұлдыздық шама –

Температура диаграммасы

Бас тізбекті жағалай төмен түскен сайын жұлдыздар массасы кеми түседі. Ергежейлілердің массасы Күннен аз. M < 0,02 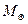болған кезде заттан жұлдыз түзіле алмайды, ол планетаға сығымдалады.

Сонымен, спектр-жарықтылық диаграммасын жұлдыздар күйінің диаграммасы деп қабылдауға болады.

3.4.7. Жұлдыздар құрылымы және жұлдыздар қойнауындағы физикалық күйлер

А) Бас тізбектің жоғарғы бөлігінің жұлдыздары.

Бұл массасы Күн массасынан үлкен жұлдыздар. Олардағы температура мен қысым кейінгі спектрлік класс жұлдыздарына қарағанда жоғары және термоядролық энергия бөлінуі көміртегі циклы арқылы жылдам жүреді. Бұдан бас тізбекте орныққан ыстық жұлдыздар жас жұлдыздар екенін білеміз.

Энергияның бөлінуі өте жоғарғы температураға байланысты (Т) және ол Стефан–Больцман заңына байланысты Т⁴ дәрежесіне байланысты өседі. Сондықтан энергияны заттың өзі тасымалдау керек және бас тізбектегі жұлдыздар қойнауында орталық конвективтік аймақтар пайда болды. Массасы 10 Күн массасындай жұлдыздардың ішкі конвективтік аймағының радиусы жұлдыз радиусының ¼ - не жуық болады, ал центріндегі тығыздық орташадан 25 есе көп. Конвективтік ядроны қоршап тұрған жұлдыздар қабаты сәулелік тепе-теңдікте болады (яғни күндегідей).

Б) Бас тізбектің төменгі бөлігіндегі жұлдыздар

Бұл жұлдыздар Күнге ұқсас.Протон-протондық реакция нәтижесінде бөлінетін энергияның қуаты температураға тәуелді. Бас тізбектің төменгі бөлігіндегі жұлдыздарда сыртқы конвективтік қабаттар пайда болады.Жұлдыз суық болған сайын қабат тереңдігі жоғары болады.Егер Күннің 2%-ке ғана конвекция қабаттары болса, ал массасы 0,6 масса ергежейлілерде аралауда бүкіл массаның 10%-ы қатысады.

В) Субергежейлілерде ауыр элементтер аз.

Субергежейлілер – кәрі жұлдыздар, олар Галактика дамуының ертеректегі кезеңдерінде пайда болды. Ауыр элементтер аз болған себепті субергежейлердің заты бас тізбектегі жұлдыздармен салыстырғанда мөлдір болып табылады, ондағы сәулелік энергия тасымалдануы жеңіл болады.

Г) Қызыл алыптардың құрылымы біртексіз болып келеді..

Жұлдыздың орталық қабаттарындағы сутегінің қызуына байланысты энергияның бөлінуі перифериялық қабаттарға ғана ығысады. Нәтижеде энергия бөлінетін жұқа қабат пайда болады, бұл қабатта сутегілік реакция жүреді. Бұл қабат жұлдызды екі бөлікке бөледі: ішкі – мұнда сутегісі жоқ «гелийлік» ядро ( ядролық реакция жоқ ) және сыртқы –мұнда сутегі бар, бірақ температура мен қысым реакция жүруіне жеткіліксіз. Алғашқыда, энергия шығаратын қабаттағы қысым ядродағыдан көп, сондықтан ол сығыла бастайды, гравитациялық энергияны бөліп қыза бастайды. Бұл қысым газ тозғындалғанша жүреді.

Д) Ақ ергежейлілер. Г – Р диаграммада бұл обьект төменгі сол жақ бұрышта орналасуы тиіс, себебі өлшемдерінің аздығынан температураның жоғарғы мәнінің өзінде де оның жарықтылығы аз болады. Жоғарғы суретте бұл ақ ергежейлілер аймағына сәйкес келетінін көреміз. Сондықтан, ақ ергежейлер аса тығыз жұлдыздар болып табылады, оның себебі термоядролық энергияның сутегілік көздері таусылған. Ақ ергежейлердің центіріндегі тығыздық 1см³-та жүздеген тоннаға дейін жетуі мүмкін. Ақырын суи отырып, олар тозғындалған газдың жылулық энергиясын сәулелей бастайды. Ақ ергежейлердің массасы өскен сайын оның қойнауындағы газ қысымы гравитациялық күшке қарсы төтеп бере алады. Сондықтан массасы үлкен ақ ергежейлер көбірек сығылады және олар үшін жұлдыз радиусының оның массасынан тәуелділігі дәлірек орындалады.

Е) Нейтронды жұлдыздар. Массаның қандайда бір мәнінен кейін тозғындалған газдың қысымы гравитация күшін теңгере алмайды. Мұндай жұлдыз шексіз сызыла береді (коллапс). Егер масса 2-3т асып түссе, онда жұлдыз коллапсқа ұшырайды. Егерде жұлдыз нейтронды болмаса, бұл құбылыс т > 1,2 m жағдайында болар еді. Себебі гравитация күштеріне тозғындалған нейтронды «газдың» қысымы қарсы тұрады. Бірақ бұған дейін жұлдызда ядролық жарылыс болады, нәтижесінде бүкіл ядролық энергиямен зат нейтрондарға айналады да жаңа обьект нейтронды жұлдыз пайда болады. Бұл жұлдыздардың беті болады. Себебі оның сыртқы қаббатары қатты болады және темір мен гелийдің ауыр элементтерінен құралады. Кәдімгі жұлдыз нейтрондық күйге дейін сығылғанда оның магнит өрісінің кернеулігі 10 бірлікке дейін өседі. Бұл кернеулік атомдар пішіндегіден 1000-даған есе көп. Нәтижесі нейтронды жұлдыздың қатты қабатының шекарасында атомдық құрылым өзгереді. 10 К температурадада нейтронды жұлдыздың бетінде атомдар бейтараптығын (нейтралдығын) жоғалтпайды (кәдімгі жағдайда мұндай температурада газ әлде қашан иондалар еді)

Ж) қара құрдымдар. Күн массасынан бірнеше көп есе массада тозғындалған нейтрондардың қысымы гравитациялық күштерге төтеп бере алмайды және жұлдыздың қайтымсыз сығылуына еш нәрсе бөгет бола алмайды (коллапс). Коллапстанушы жұлдыздың радиусы қандайда бір кризистік радиусқа (R) жақындағанда ерекше жағдай орындалады, R былайша анықталады: R=2c*m/r. Радиусы гравитациялық радиустан аз жұлдыздан жарық сәулелері шыға алмайды. Мұндай обьект физика заңдарына сәйкес өмір сүру керек деп есептегенімен, ол байқалмайды. Бұл, теориялық түрде жорамалданған жарықты жұтушы және өзіне басқа массаларды тартып алатын, сәуле шығармайтын обьектілер қара құрдымдардеп атайды. Шварцшильд радиусымен шектелген сфера ішінде заттың тығыздығы шексіз өсіп классикалық физика заңдары орындалмайды, мұнда тек жалпы салыстырмалық теория немесе релятивистік физика заңдары жұмыс істейді. Сондықтан нейтронды жұлдыздармен қатар қара құрдымдарды релятивистік обьект деп атайды.

3.4.8. Қос жұлдыздар

Аспанда екі немесе бірнеше біріне-бірі жақын орналасқан жұлдыздар жиі кездеседі, олардың кейбіреулері шын мәнінде бір-бірінен өте алыста орналасады және олардың физикалық сипаттамалары да түрліше болады. Олар тек аспан сферасындағы жақын нүктелерге проекцияланады, сол себепті оларды оптикалық қос жұлдыздар деп атайды. Бұлардан өзгеше, физикалық қос жұлдыздардеп атайтын жүйелер бар, олар ортақ динамикалық жүйе құрып тартылыс күші нәтижесінде ортақ масса центрі бойымен айналады. Кейде үш немесе оданда көп жұлдыздардың бірігуі де бақыланады. Егер қос жұлдыздардың компонеттері өзара алыс орналасса, яғни олар бөлектеніп көрінсе, онда ондай жұлдыздарды визуалды қос жұлдыздардеп атайды. Кейбір тығыз орналасқан жұлдыздардың компоненттері жекелей көрінбейді, олар тек фото түрде ғана ажыратылады (тұтылған айнымалы жұлдыздар) және спектрлері арқылы ғана ажыратылады (спектірлі қос жұлдыздар).

3.4.9. Қос жүйелердің жалпы сипаттамалары

Қос жұлдыздар табиғатта жиі кездеседі сондықтан ол зерттеу жұлдыздардың өзінің ғана емес жалпы жұлдыздар пайда болуы мен эволюциясының космогониялық проблемаларын шешуде де маңызды. Зерттеліп отырған жүйе оптикалық қос жұлдыз емес нағыз физикалық екендігіне көз жеткізу үшін ұзақ уақыт бақылаулар жүргізу керек. Жұлдыздардың физикалық жүйе екендігі олардың өздерінің қозғалысынан анғаруға болады. Қазіргі кезде онмыңдаған тығыз визуалды қос жұлдыздардың бар екендігі белгілі.

Қос жұлдыздар компоненттерінің қозғалысы Кеплер заңына сәйкес жүреді, яғни екі компанентте кеңістікте ортақ масса центіріне қатысты эллипстік орбиталар сызады. Егер бас жұлдыз қозғалмайды десек, онда серік–жұлдыздың эксцентриситеті де Кеплер заңына сәйкес алынады. Серік-жұлдыздың бас жұлдызға қатысты салыстырмалы қозғалыс орбитасының үлкен жарты осі екі жұлдыздың ортақ масса центріне қатысты қозғалыс орбиталарының үлкен жарты осьтерінің қосындысына тең. Екінші жағынан,бұл екі эллипстің үлкен жарты осьтерінің шамасы жұлдыздар массасына кері пропорционал. Егер бақылау нәтижесінде салыстырмалы қозғалыс орбитасы белгілі болса, онда белгілі өрнектерді пайдаланып қос жұлдыздар компоненттерінің энергиясын анықтауға болады. Егер олардың орбиталарының жарты осьтерінің қатынасы белгілі болса, онда массалар қатынасын да табуға болады, яғни әр бар жұлдыздың массасын жеке – жеке анықтауға болады.Қос жұлдызды зерттеудің маңыздылығының бірі осы,,яғни негізгі шамалардың бірі – жұлдыз массасын анықтау,ал масса арқылы жұлдыздың ішкі құрылысын және оның атмосферасын зерттеуге болады.

3.4.10. Визуалды қос жұлдыздар

Қосарлылығы тек телескоп арқылы анықтайтын қос жұлдыздар – визуалды қос жұлдыздар деп атайды. Серік жұлдыздың бас жұлдызға қатысты көрінетін орбитасын ұзақ уақыт бақылаулар арқылы анықталады. Бұл орбиталар эллипс пішінді болады.

Визуалды қос жұлдыздың көрінетін орбитасы оның шын орбитасының жазықтыққа проекциясы болып табылады. Сондықтан орбитаның барлық элементтерін анықтау үшін ең алдымен еңкею бұрышын білу керек. Бұл бұрышты жұлдыздардың еңкеюін бұрышын көрінгенде ғана анықтауға болады. Егер еңкею бұрышы, периастр бойлығы болса , онда бұл элементтерді анықтау геометриялық есеп болып табылады. Орбитаның үлкен жарты осьінің шын мәнін а және а келесі өрнекпен байланысқан:

А және а бұрыштық өлшеммен анықталады.

Қазіргі кезде алпыс мыңнан аса визуалды қос жұлдыздар тіркелген. Бұлардың шамамен екі мың орбиталарының қозғалыстары анықталған.

3.4.11. Тұтылған айнымалы жұлдыздар

Тұтылған айнымалылар деп телескоппен ажыратылмайтын тығыз жұлдыздар жұбын айтады. Бұл жағдайда жарықтылығы жоғары жұлдыз – бас жұлдыз, ал төменгі – серік жұлдыз болып табылады. Бұл жұлдыздарға, мысалы Алголь және Лираның β-сы жатады. Бас жұлдыздың серік жұлдызбен үнемі тұтылуы нәтижесінде жұлдыздардың тұтылған айнымалыларының шамасы периодты түрде өзгеріп отырады. Жұлдыздардың сәулелену ағынының уақыт бойынша өзгеруі жылтырлық қисығы деп аталады. Жұлдыздың ең аз көрінетін жұлдыздық шамасы кезіндегі уақыт мезеті – максимум кезеңі, ал қарсы жағдайдағысы – минимум кезеңі деп аталады.

Тұтылған айнымалы жұлдыздың жылтырлық қисығының сипаты бойынша қос жұлдыздың біреуінің екіншісіне қатысты орбита элементтерін анықтауға болады. Жылтырлақ қисығын мұқият зерттеу нәтижесінде тұтылған айнымалы жұлдыздар туралы келесі мәліметтер алынады:

1. Тұтылу сипаты көлбеулік бұрышы мен жұлдыздың өлшемдері көмегімен анықталады: i = 90^º болғанда тұтылу орталық болады.

2. Минимумдардың ұзақтығының негізінде компоненттердің R₁ және R₂ радиустарын табуға болады

3. Егер тұтылу толық болса, онда минимумдар тереңдігенің қатынасы арқылы жарықтылықтар қатынасын анықтауға болады, ал егер радиустары белгілі болса онда температуралардың қатынасын анықтай аламыз.

4. Жылтырлық қисығының көлбеулік сипатынан жұлдыздар сәулеленулерінің өзара шағылуларын сипаттауға болады.

5. Жылтырлық қисығының минимумдарын мұқият зерттеу нәтижесінде жұлдыз дискінің шетіне қарай қараңғылау заңын бағалауға болады.

Сонымен, жылтырлық қисығының нәтижесінде келесі шамаларды анықтауға болады екен: i - орбита жазықтығының көлбеулік бұрышы, Р – айналу периоды, Т – бас минимум кезеңі, е – орбита эксцентриситеті, w - периастр бойлығы, R₁,R₂ - компоненттердің радиустары, L₁/L₂- жарықтылықтар қатынасы.

3.4.12. Спектрлі қос жұлдыздар

Кейбір жұлдыздардың спектрлерінде периодтық қосарлану байқалады. Егер бұл жұлдыздар тұтылған айнымалылар болса, онда сызықтардың тербеліс периодтары бірдей болады. Бұл жағдайда, яғни бірігу мезеттерінде спектрлік сызықтардың ортаңғы орнынан ауытқуы нөлге тең. Ал, басқа мезеттерде спектрлік сызықтардың қосарлануы байқалады. Компоненттердің сәулелік шамасы неғұрлым жоғары мәнде болса, қосарлану мәні де соғұрлым жоғары болады. Егер алынған спектр бір ғана жұлдызға тән болса (екіншісінің спектрі оның әлсіздігі салдарынан көрінбейді), онда сызықтардың қосарлануының орнына олардың спектрлерінің бірде қызыл, ал бірде көк бөлігіне ығысуы байқалады. Сәулелік жылдамдықтар қисығы тек екі параметр арқылы анықталады: орбита эксцентреритеті ежәне периастр бойлығы w. Қосарлығы тек спектрлік бақылаулар нәтижесінде ғана анықталатын жұлдыздар спектрлік-қос жұлдыздар деп аталады. Тұтылған айнымалыларға қарағанда бұл жұлдыздарды ίбұрышы 90°-тан қатты ауытқыған жағдайда да бақылауға болады.

Қазіргі кезде шамамен 2500-дей спектрлік-қос жұлдыздар бар екені белгілі. Олардың 750-нің ғана сәулелік жылдамдықтар қисығы белгілі. Ал сәулелік жылдамдықтар қисығының көмегімен бұл жұлдыздардың айналу периодтары мен орбиталарының пішіндерін анықтауға болар еді.

3.4.13. Физикалық айнымалы жұлдыздар

Физикалық айнымалы жұлдыздар деп физикалық процестер нәтижесінде жарықтылықтары аз уақыт аралығында өзгеріп отыратын жұлдыздарды айтады. Айнымалылығының сипатына қарай жұлдыздар пульсациялайтын және эруптивті айнымалылар, жаңа және аса жаңа (эруптивтінің дербес жағдайлары) болып бөлінеді. Барлық айнымалы жұлдыздар арнайы әріптермен белгіленеді (R,S,T,….,Z, ZZ, RR,…., RZ,ST,…. ,AA) және бұған қоса шоқжұлдыздардың аттары қосылып жазылады, мысалы: RR Lyz,...).