Характеристики электромагнитных волн.
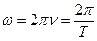 - циклическая частота;
- циклическая частота;
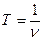 - период колебаний;
- период колебаний;
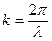 - волновое число;
- волновое число;
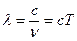 - длина волны;
- длина волны;
с – скорость электромагнитных волн в вакууме;
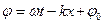 - фаза волны;
- фаза волны;
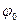 - начальная фаза.
- начальная фаза.
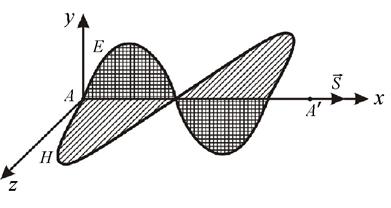
Рис. 1
Уравнения (3) и (4) описывают плоские монохроматические электромагнитные волны (электромагнитные волны одной строго определенной частоты), причем мгновенные значения векторов 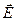 и
и 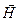 в любой точке связаны соотношением
в любой точке связаны соотношением
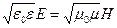 , (5)
, (5)
где ε0=8,85•10-12 Ф/м – электрическая постоянная;
ε – диэлектрическая проницаемость среды;
μ0=4π•10-7 Гн/м – магнитная постоянная;
μ – магнитная проницаемость среды.
Фазовая скорость электромагнитных волн определяется выражением
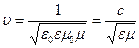 , (6)
, (6)
где 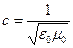 - скорость электромагнитных волн в вакууме.
- скорость электромагнитных волн в вакууме.
В вакууме (при ε=1 и μ=1) скорость распространения электромагнитных волн совпадает со скоростью с. Так как εμ>1, то скорость распространения электромагнитных волн в веществе всегда меньше, чем в вакууме.
Электромагнитные волны поперечны, т. е. векторы 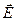 и
и 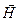 напряженностей электрического и магнитного полей волны взаимно перпендикулярны и лежат в плоскости, перпендикулярной вектору скорости
напряженностей электрического и магнитного полей волны взаимно перпендикулярны и лежат в плоскости, перпендикулярной вектору скорости 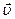 распространения волны, причем векторы
распространения волны, причем векторы 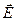 ,
, 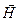 и
и 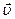 образуют правовинтовую систему.
образуют правовинтовую систему.
Вектор плотности потока электромагнитной энергии называется вектором Умова-Пойнтинга:
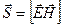 . (7)
. (7)
Вектор 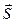 направлен в сторону распространения электромагнитной волны.
направлен в сторону распространения электромагнитной волны.
Интерференцией светаназывается явление усиления волн в одних точках пространства и ослабление их в других в результате наложения двух или нескольких световых волн. Пространство, в котором волны накладываются и интерферируют, называют интерференционным полем.
Если в интерференционное поле поместить отражающий экран, то на нем будет наблюдаться интерференционная картина, представляющая собой набор чередующихся полос с максимальной и минимальной освещенностью. Устойчивую во времени и достаточно контрастную интерференционную картину дают только одинаково поляризованные когерентные волны, т.е. волны с взаимно параллельными векторами 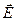 одинаковой частотой и постоянной во времени разностью фаз.
одинаковой частотой и постоянной во времени разностью фаз.
Интерференционную картину, создаваемую когерентными волнами, можно наблюдать визуально, фотографировать, измерять расстояние между светлыми и темными полосами и т.д. Некогерентные лучи не дают стабильной интерференционной картины. Непрерывное изменение фаз складываемых колебаний в каждой точке пространства создает быстро меняющуюся картину, которую невозможно использовать для измерительных целей.
Для получения устойчивой интерференционной картины применяют различные приемы, но все они сводятся к образованию и наложению одинаково поляризованных когерентных волн.
Опыт Юнга.
Юнг был первым, кто понял, что волны от двух разделённых в пространстве и независящих друг от друга источников света не когерентны. Поэтому он пропустил в тёмную комнату солнечный свет через узкую щель 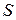 (шириной около 1 мкм), затем с помощью двух щелей
(шириной около 1 мкм), затем с помощью двух щелей 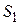 и
и 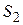 такой же ширины, находящихся друг от друга на расстоянии
такой же ширины, находящихся друг от друга на расстоянии 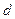 порядка нескольких микрон, разделил этот пучок света на два (рис.2). Проходя через каждую из щелей, световой пучок расширялся вследствие дифракции, поэтому на белом экране Э световые пучки, прошедшие через щели
порядка нескольких микрон, разделил этот пучок света на два (рис.2). Проходя через каждую из щелей, световой пучок расширялся вследствие дифракции, поэтому на белом экране Э световые пучки, прошедшие через щели 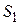 и
и 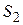 , перекрывались. В области перекрытия световых пучков наблюдалась устойчивая интерференционная картина в виде чередующихся светлых и темных полос. В центре экрана видна полоса белого солнечного света. Остальные интерференционные максимумы окрашены.
, перекрывались. В области перекрытия световых пучков наблюдалась устойчивая интерференционная картина в виде чередующихся светлых и темных полос. В центре экрана видна полоса белого солнечного света. Остальные интерференционные максимумы окрашены.
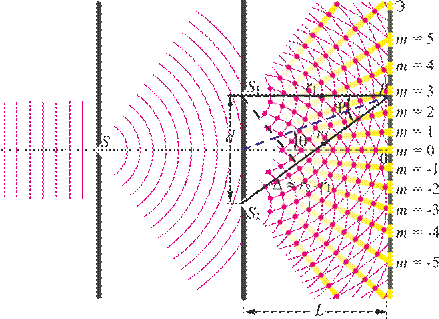
Рис. 2
Таким образом, в классическом опыте Юнга когерентные световые пучки были получены путём разделения и последующего сведения лучей, исходящих от общего источника света.
Зеркало Ллойда.
В опыте, предложенном ирландским физиком Хэмфри Ллойдом (1800-1881 гг.), источником света 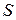 служит узкая щель, параллельная плоскости зеркала (рис.3). Расходящийся световой пучок от источника падает на плоское зеркало
служит узкая щель, параллельная плоскости зеркала (рис.3). Расходящийся световой пучок от источника падает на плоское зеркало 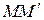 (зеркало Ллойда), расположенное перпендикулярно к экрану
(зеркало Ллойда), расположенное перпендикулярно к экрану 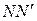 . Отразившись от зеркала, он попадает на экран. Этот пучок света можно представить исходящим от мнимого изображения источника света
. Отразившись от зеркала, он попадает на экран. Этот пучок света можно представить исходящим от мнимого изображения источника света 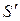 , образованного зеркалом. Кроме того, на экран попадают лучи, идущие непосредственно от источника света
, образованного зеркалом. Кроме того, на экран попадают лучи, идущие непосредственно от источника света 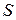 . В той области экрана, где перекрываются оба пучка света, т.е. накладываются две когерентные волны, наблюдается интерференционная картина.
. В той области экрана, где перекрываются оба пучка света, т.е. накладываются две когерентные волны, наблюдается интерференционная картина.

Рис. 3
Особенность интерференционной картины, наблюдаемой с помощью зеркала Ллойда, заключается в том, что центральная полоса получается не светлой, а темной. Это указывает на то, что лучи, проходящие одинаковые геометрические пути, все же сходятся в опыте Ллойда с разностью хода 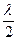 . Такая «потеря» полуволны (или, другими словами, изменение фазы на π) происходит при отражении света от поверхности стекла, коэффициент преломления которого больше, чем воздуха.
. Такая «потеря» полуволны (или, другими словами, изменение фазы на π) происходит при отражении света от поверхности стекла, коэффициент преломления которого больше, чем воздуха.
Зеркала Френеля.
Френель предложил в качестве двух когерентных источников воспользоваться двумя изображениями одного и того же действительного источника света 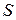 в двух плоских зеркалах
в двух плоских зеркалах 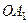 и
и 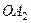 , образующих двугранный угол
, образующих двугранный угол 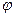 , отличающийся от 180° всего на несколько угловых минут. Схема опыта Френеля представлена на рисунке 4 (
, отличающийся от 180° всего на несколько угловых минут. Схема опыта Френеля представлена на рисунке 4 ( 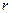 – расстояние от источника света до места соприкосновения зеркал).
– расстояние от источника света до места соприкосновения зеркал).

Рис. 4
Для построения изображений источника 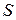 в обоих зеркалах воспользуемся тем, что мнимое изображение, даваемое плоским зеркалом, лежит за зеркалом на таком же расстоянии, на каком источник расположен перед зеркалом. Проведем из точки
в обоих зеркалах воспользуемся тем, что мнимое изображение, даваемое плоским зеркалом, лежит за зеркалом на таком же расстоянии, на каком источник расположен перед зеркалом. Проведем из точки 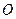 окружность с радиусом
окружность с радиусом 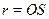 и опустим из точки
и опустим из точки 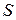 перпендикуляр на продолжение прямой
перпендикуляр на продолжение прямой 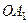 . Точка пересечения продолжения этого перпендикуляра с окружностью
. Точка пересечения продолжения этого перпендикуляра с окружностью 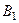 является мнимым изображением источника
является мнимым изображением источника 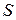 в первом зеркале
в первом зеркале 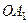 . Аналогично строится мнимое изображение
. Аналогично строится мнимое изображение 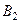 источника во втором зеркале
источника во втором зеркале  .
.
На экране, где пучки, отражённые от зеркал, перекрываются, наблюдается интерференционная картина в виде равноотстоящих тёмных и светлых полос.
Бипризма Френеля.
Бипризма Френеля состоит из двух стеклянных призм, соединенных боковыми сторонами. Схема опыта представлена на рисунке 5 ( 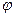 – преломляющий угол призмы;
– преломляющий угол призмы; 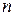 – абсолютный показатель преломления материала призмы).
– абсолютный показатель преломления материала призмы).
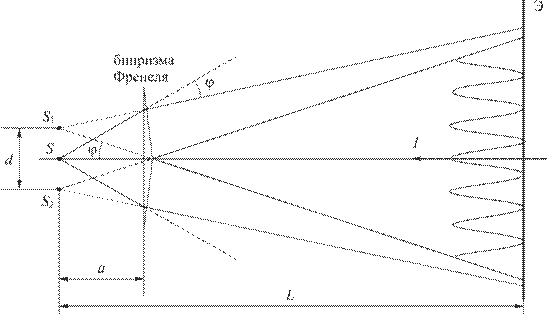
Рис. 5
Свет от источника 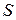 преломляется в обеих призмах, в результате чего за призмой распространяются пучки, как бы исходящие от мнимых источников
преломляется в обеих призмах, в результате чего за призмой распространяются пучки, как бы исходящие от мнимых источников 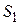 и
и 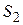 , разнесённых на расстояние
, разнесённых на расстояние 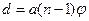 и являющихся когерентными. На экране, расположенном за бипризмой эти пучки интерферируют.
и являющихся когерентными. На экране, расположенном за бипризмой эти пучки интерферируют.
Закономерности интерференции. Расчет электромагнитного поля ведут обычно по вектору 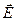 , поскольку зрительные органы человека не реагируют на магнитную составляющую поля.
, поскольку зрительные органы человека не реагируют на магнитную составляющую поля.
Произведем расчет интерференционной картины от двух когерентных источников S1 и S2 (рис. 6).
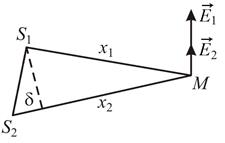
Рис. 6
Предположим, что две монохроматические световые волны, накладываясь друг на друга, возбуждают в точке М пространства колебания векторов напряженности электрического поля, мгновенные значения которых:
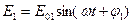 , (8)
, (8)
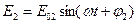 , (9)
, (9)
где 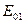 и
и 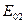 – амплитуды напряженностей электромагнитных колебаний в точке М;
– амплитуды напряженностей электромагнитных колебаний в точке М; 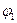 и
и 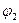 - начальные фазы.
- начальные фазы.
Амплитуду результирующего колебания 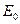 легко найти с помощью векторной диаграммы, изображенной на рис. 7.
легко найти с помощью векторной диаграммы, изображенной на рис. 7.
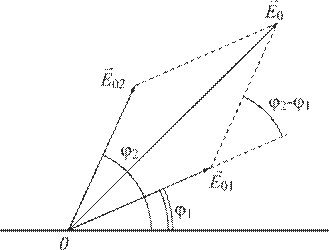
Рис. 7
По теореме косинусов
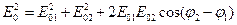 . (10)
. (10)
Учитывая, что интенсивности волн, пропорциональны квадратам их амплитуд, выразим интенсивность результирующего колебания по формуле
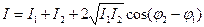 . (11)
. (11)
Так как в реальных некогерентных источниках излучателями являются отдельные атомы, не связанные друг с другом, то разность фаз 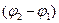 непрерывно изменяется, принимая с равной вероятностью любые значения, так что среднее по времени значение
непрерывно изменяется, принимая с равной вероятностью любые значения, так что среднее по времени значение 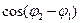 равно нулю. В этом случае интенсивность волны во всех точках экрана
равно нулю. В этом случае интенсивность волны во всех точках экрана 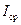 равна сумме интенсивностей складываемых волн
равна сумме интенсивностей складываемых волн
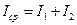 . (12)
. (12)
Интенсивность света во всех точках экрана просто равна сумме интенсивностей, что соответствует закону сохранения энергии. Поэтому при сложении некогерентных волн интерференция не возникает.
Если же разность фаз возбуждаемых волнами колебаний равна нулю или остается постоянной во времени, то волны являются когерентными. Источники таких волн также когерентны. В этом случае 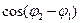 имеет постоянное во времени, но свое для каждой точки экрана значение, в результате чего в одних местах возникают максимумы интенсивности, а в других – минимумы, т.е. наблюдается интерференционная картина.
имеет постоянное во времени, но свое для каждой точки экрана значение, в результате чего в одних местах возникают максимумы интенсивности, а в других – минимумы, т.е. наблюдается интерференционная картина.
Рассмотрим случай сложения когерентных колебаний от двух синфазных источников 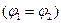 .
.
При 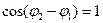 , т.е. при
, т.е. при
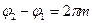 , (13)
, (13)
где m=0,1,2... – целое число, называемое порядком интерференционного максимума, интенсивность результирующего колебания будет максимальна и равна
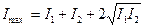 . (14)
. (14)
При 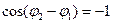 , т.е. при
, т.е. при
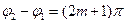 , (15)
, (15)
интенсивность результирующего колебания будет минимальной:
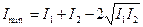 . (16)
. (16)
Разность 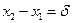 называют геометрической разностью хода волн, разность
называют геометрической разностью хода волн, разность 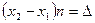 - оптической разностью хода волн, приходящих в точку M от источников
- оптической разностью хода волн, приходящих в точку M от источников 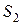 и
и 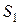 ( n – показатель преломления среды).
( n – показатель преломления среды).
Принимая во внимание, что 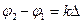 , где
, где 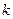 – волновое число, получим условия возникновения максимумов и минимумов интенсивности результирующей волны в виде:
– волновое число, получим условия возникновения максимумов и минимумов интенсивности результирующей волны в виде:
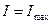 , если
, если 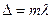 , (m=0,1,2,…), (17)
, (m=0,1,2,…), (17)
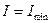 , если
, если 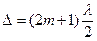 , (m=0,1,2,…). (18)
, (m=0,1,2,…). (18)
Интерференционные максимумы наблюдаются в точках пространства, для которых оптическая разность хода интерферирующих волн равна целому числу длин волн или четному числу длин полуволн (формула (17)).
Интерференционные минимумы наблюдаются в точках пространства, для которых оптическая разность хода интерферирующих волн равна нечётному числу длин полуволн (формула (18)).
Формулы (13) и (15) выражают условия максимумов и минимумов интерференционной картины через разность фаз.
Пусть источники когерентных волн 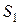 и
и 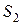 находятся друг от друга на некотором расстоянии d (рис. 8).
находятся друг от друга на некотором расстоянии d (рис. 8).
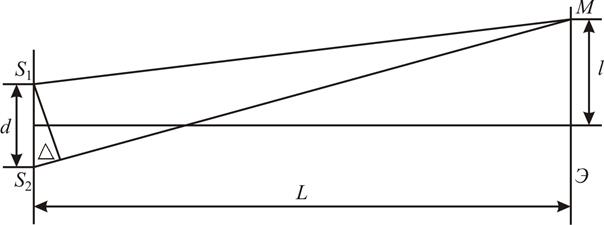
Рис. 8
Экран Эустановлен от источников на расстоянии 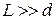 . На экране будет наблюдаться интерференционная картина, и освещенность экрана в некоторой точке M будет зависеть, как это было показано выше, от разности хода
. На экране будет наблюдаться интерференционная картина, и освещенность экрана в некоторой точке M будет зависеть, как это было показано выше, от разности хода 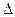 . Получим формулу для вычисления разности хода. Как видно из рис. 8, при условии, что d и l много меньше L, можно записать
. Получим формулу для вычисления разности хода. Как видно из рис. 8, при условии, что d и l много меньше L, можно записать 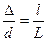 , или
, или
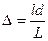 . (19)
. (19)
Так как 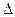 пропорциональна l, то с ростом l периодически будут выполняться то условия минимума, то максимума, и на экране будет наблюдаться интерференционная картина в виде периодически чередующихся темных и светлых полос.
пропорциональна l, то с ростом l периодически будут выполняться то условия минимума, то максимума, и на экране будет наблюдаться интерференционная картина в виде периодически чередующихся темных и светлых полос.
Явление интерференции света широко применяется в технике в частности, для прецизионных измерений длин, углов, оценки качества обработки поверхности и др.
2. ОПИСАНИЕ ИНТЕРФЕРОМЕТРА
И МЕТОДИКА ИЗМЕРЕНИЙ
Оптические измерительные приборы, действие которых основано на использовании интерференции света, называют интерферометрами. Для получения двух когерентных световых волн в интерферометрах используют светоделитель, выполненный либо в виде полупрозрачного зеркала, либо в виде призмы-куба с полупрозрачной гипотенузой. Светоделитель расщепляет световую волну на две части – отраженную и прошедшую через него. Полученные таким образом когерентные волны проходят различные оптические пути, отражаются от специальных зеркал и с помощью того же светоделителя направляются в объектив микроскопа или зрительной трубы, с помощью которых и наблюдают интерференционную картину. На рис. 9 показана оптическая схема интерферометра Линника. В качестве светоделителя в интерферометре используется призма-куб с полупрозрачной гипотенузой. Роль одного из зеркал выполняет изучаемая поверхность.
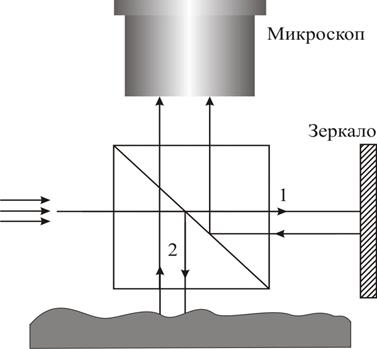
Исследуемая поверхность
Рис. 9
Плоская световая волна (параллельный пучок света) от источника направляется на светоделитель и разделяется им на две волны 1 и 2 .
Первая волна, отразившись от зеркала и от полупрозрачной гипотенузы светоделителя, попадает в объектив микроскопа. Вторая волна, отразившись от исследуемой поверхности и пройдя сквозь посеребренную гипотенузу куба, также поступает в микроскоп. Эти волны когерентны и интерферируют. В микроскопе наблюдается интерференционная картина. Ее характер определяется разностью хода, возникающая при прохождении волн (пучков) 1 и 2 от полупрозрачной гипотенузы куба до соответствующих зеркал и обратно. Если исследуемая поверхность – идеально плоское зеркало, установленное перпендикулярно основному зеркалу, то все поле зрения микроскопа будет ровно освещено, т.к. в любой его точке обе волны будут иметь одну и ту же разность хода. Степень освещенности поля микроскопа будет зависеть от того, чему равна эта разность хода. Если 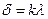 , то освещение максимально, а если
, то освещение максимально, а если 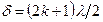 , то поле темное. Если одно из зеркал повернуть на небольшой угол, то разность хода волн будет линейно изменяться от точки к точки поверхности этого зеркала и в микроскопе будет наблюдаться интерференционная картина в виде чередующихся светлых и темных полос. Если исследуемая поверхность имеет дефекты, то в местах выступов или впадин интерференционные полосы искривляются. Искривление полос вызывается изменением длины пути, проходимого световой волной при ее отражении от впадин или выступов. Величина искривления полос тем больше, чем больше высота неровности или глубина царапины (рис. 10).
, то поле темное. Если одно из зеркал повернуть на небольшой угол, то разность хода волн будет линейно изменяться от точки к точки поверхности этого зеркала и в микроскопе будет наблюдаться интерференционная картина в виде чередующихся светлых и темных полос. Если исследуемая поверхность имеет дефекты, то в местах выступов или впадин интерференционные полосы искривляются. Искривление полос вызывается изменением длины пути, проходимого световой волной при ее отражении от впадин или выступов. Величина искривления полос тем больше, чем больше высота неровности или глубина царапины (рис. 10).
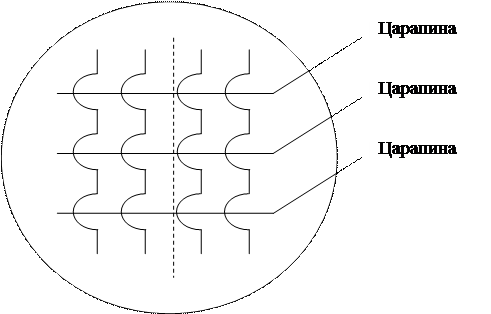 |
Рис. 10
В данной работе используется микроинтерферометр Линника МИИ-4, предназначенный для визуальной оценки, а также измерений и фотографирования высоты неровностей обработанных поверхностей.
В поле зрения микроинтерферометра МИИ-4 видны одновременно исследуемая поверхность и интерференционные полосы [при использовании полихроматического (белого) света - это цветные линии].
Измерение величины искривления и расстояния между полосами (интервала или периода интерференционной картины) осуществляется винтовым окулярным микрометром МОВ-1-15 , который прилагается к интерферометру.
Прибор МИИ-4 позволяет измерять высоты неровностей в пределах от 1 до 30 мкм, что соответствует чистоте обработки поверхности от 10 до 14 класса включительно по ГОСТ 2789–73 (всего, в зависимости от качества обработки, поверхности оцениваются по ГОСТу 14 классами шероховатости).
3. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
НА МИКРОИНТЕРФЕРОМЕТРЕ
Дата добавления: 2016-10-07; просмотров: 4556;











