Парадокс Дня рождения (Birthday Paradox)

Многие криптоаналитические атаки построены на базе, так называемой, задачи парадокса дня рождения [73]. Эта задача состоит в нахождении минимального размера группы людей, такой чтобы, по меньшей мере, двое из них имели с высокой вероятностью общий день рождения. Допустим, что дни рождения r людей образуют случайную выборку размером r из набора всех дней в году. Годы не имеют равную длину, и дни рождения не постоянны на протяжении года. Однако, как приближение, случайная выборка людей принимается эквивалентной случайной выборке дней рождения. Рассмотрим год из 365 дней. Решение находится путем рассмотрения дополнительной задачи - оценки вероятность того, что все r дней рождения будут различными. Легко понять, что эта вероятность будет равна

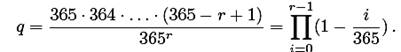
Таким образом, вероятность того, что, по меньшей мере, два человека из группы людей из r = 23 человека будут иметь общий день рождения, равна 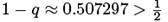. Очевидный парадокс возникает при малом числе людей, что может показаться противоестественным.

Связанная задача (Мэйера и Матиса [162]), которая использует парадокс дня рождения, формулируется так: для заданного множества X и случайной функции 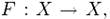найти минимальный размер двух подмножеств A и B множества X , при котором возникает коллизия между их элементами с вероятностью, выше 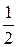. Коллизия для F представляется как пара (a,b) с 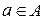, 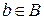такими, что F(a) = F(b), a ¹ b. Рассмотрим сначала вероятность отсутствия коллизии между подмножествами A и B, которая может быть записана как:

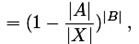
Pr(отсутствие коллизий)

которая, если |A|намного меньше |X|, равна приблизительно 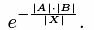Тогда вероятность появления, по меньшей мере, одной коллизии равна:

Pr (минимум, одна коллизия) = 1 - Pr (отсутствие коллизий) =

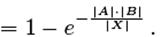
Если 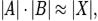то Pr (по меньшей мере, одной коллизии) = 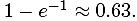Для минимизации размера подмножеств компромиссным решением будет установление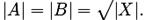

Контрмерой для атак на базе парадокса дня рождения является увеличение |X|до достаточно высокого значения, с учетом уменьшения сложности пропорциональной квадратному корню из |X|. Вследствие указанного минимального размера подмножеств ( 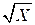), атаки на основе парадокса дня рождения иногда называются атаками квадратного корня.

Как этот парадокс относится к криптографии? Положим для атаки на 64-битный блочный шифр сопернику нужно получить две плайнтекст/шифр-текстовых пары, которые отличаются только в наименее значимом бите. Интерпретация этой задачи в терминах задачи о парадоксе дня рождения приводит к выводу, что пространство из около 2³² известных открытых текстов с высокой вероятностью будет содержать необходимую пару. Как другой пример рассмотрим цикл 64-битового Фейстелева шифра. Положим, что в шифре использована случайная F-функция (32 в 32 бита). Нападающий может захотеть узнать, как много ему необходимо получить открытых текстов для того, чтобы наблюдать равенство выходов (столкновение) F-функции. Ответом, предусмотренным парадоксом дня рождения, есть - только O(2¹⁶) текстов.

Одним из последствий парадокса дня рождения является то, что для n-битового блочного шифра, повторяемые появления блока шифртекста могут ожидаться с вероятностью около 0.63, если более чем 2ⁿ^/2 + 1 случайных открытых текстов зашифрованы на одном ключе (Кнудсен [113]), независимо от размера ключа. Для CBC режима, при совпадении двух блоков шифртекста C_i = C_j соответствующие входные данные (блоки) для функции шифрования E_k( ) также будут равны, . 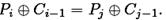Это означает, что в атаке только с шифртекстом 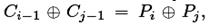то есть, информация об открытых текстах раскрывается из шифртекстовых блоков.