Термы щелочных металлов
Во многие формулы, в частности для энергии, входят не сами магнитные моменты, а их проекции. Поэтому обычно говорят, что спин электрона равен половине (в единицах 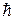 ), а спиновой магнитный момент – магнетону Бора.
), а спиновой магнитный момент – магнетону Бора.
Момент импульса электрона в атоме натрия (равный моменту всего атома) слагается из спинового и орбитального. По квантовым правилам сложения величина суммарного момента определяется квантовым числом 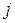 результирующего момента импульса электрона
результирующего момента импульса электрона
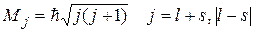 . (36.6)
. (36.6)
С механическими моментами связаны магнитные, которые могут взаимодействовать. Грубо взаимодействие спинового и орбитального магнитных моментов можно представлять себе как взаимодействие двух магнитных стрелок. Вполне очевидно, что энергия взаимодействия спинового и орбитального магнитных моментов (спин-орбитального взаимодействия) зависит от их взаимной ориентации, которая на квантовом языке описывается квантовым числом 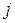 . Следовательно, состояния с различными числами j должны обладать различной энергией, а у энергетических уровней и спектров, возникающих при переходах между такими уровнями, появляется тонкая структура.
. Следовательно, состояния с различными числами j должны обладать различной энергией, а у энергетических уровней и спектров, возникающих при переходах между такими уровнями, появляется тонкая структура.
В соответствии с двумя возможными по формуле (36.6) значениями j , каждый терм ряда р, для которого l = 1, распадается на два, отвечающих 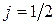 и
и 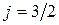 . Точно также каждый терм ряда d (
. Точно также каждый терм ряда d (  ) расщепляется на два с
) расщепляется на два с 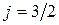 и
и  . Не расщепляются термы ряда s, (
. Не расщепляются термы ряда s, (  ), поскольку имеют только одно значение квантового числа результирующего момента импульса
), поскольку имеют только одно значение квантового числа результирующего момента импульса 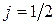 .
.
Термы атомов щелочных металлов можно обозначить символами  , в которых буква (
, в которых буква ( 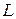 ) указывает на значение азимутального квантового числа (
) указывает на значение азимутального квантового числа (  ) для данного ряда термов, верхний индекс – мультиплетность терма (т.е. количество компонент), а нижний правый индекс – значение квантового числа результирующего момента импульса валентного электрона. Поэтому дублетные термы атомов щелочных металлов можно обозначить следующим образом:
) для данного ряда термов, верхний индекс – мультиплетность терма (т.е. количество компонент), а нижний правый индекс – значение квантового числа результирующего момента импульса валентного электрона. Поэтому дублетные термы атомов щелочных металлов можно обозначить следующим образом:
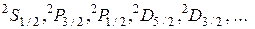
При переходах атомов между различными состояниями на изменения квантового числа результирующего момента импульса j накладывается правило отбора:
 . (36.8)
. (36.8)
Релятивистская квантовая теория дает для расстояния между подуровнями тонкой структуры водородного атома значение
 . (36.9)
. (36.9)
где  энергия ионизации атома водорода;
энергия ионизации атома водорода;
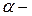 постоянная тонкой структуры:
постоянная тонкой структуры: 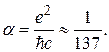
Постоянная тонкой структуры характеризует энергию взаимодействия двух электронов, выражается через и принадлежит к числу фундаментальных констант природы.
Дата добавления: 2021-01-11; просмотров: 443;











