Классификация задач принятия решений

Задачи принятия решений отличаются большим многообразием, классифицировать их можно по различным признакам, характеризующим количество и качество доступной информации. В общем случае задачи принятия решений можно представить следующим набором информации [8, 17, 18]:

<Т, A, К, X, F,G, D>,

где Т— постановка задачи (например, выбрать лучшую альтернативу или упорядочить весь набор);

А — множество допустимых альтернативных вариантов;

К— множество критериеввыбора;

Х— множество методов измерения предпочтений (например, использование различных шкал);

F— отображение множества допустимых альтернатив в множество критериальных оценок (исходы);

G — система предпочтений эксперта;

D — решающее правило, отражающее систему предпочтений.

Любой из элементов этого набора можетслужить классификационным признаком принятия решений.

Рассмотрим традиционные классификации:

1. По виду отображения F. Отображение множества А и К может иметь детерминированный характер, вероятностный или неопределенный вид, в соответствии с которым задачи принятия решений можно разделить на задачи в условиях риска и задачи в условиях неопределенности.

2. Мощность множества К. Множество критериев выбора может содержать один элемент или несколько. В соответствии с этим задачи принятия решений можно разделить на задачи со скалярным критерием и задачи с векторным критерием (многокритериальное принятие решений).

3. Тип системы G. Предпочтения могут формироваться одним лицом или коллективом, в зависимости от этого задачи принятия решений можно классифицировать на задачи индивидуального принятия решений и задачи коллективного принятия решений.

Задачи принятия решений в условиях определенности.К этому классу относятся задачи, для решения которых имеется достаточная и достоверная количественная информация. В этом случае с успехом применяются методы математического программирования, суть которых состоит в нахождении оптимальных решений на базе математической модели реального объекта. Основные условия применимости методов математического программирования следующие:

1. Задача должна быть хорошо формализована, т. е. имеется адекватная математическая модель реального объекта.

2. Существует некоторая единственная целевая функция (критерий оптимизации), позволяющая судить о качестве рассматриваемых альтернативных вариантов.

3. Имеется возможность количественной оценки значений целевой функции.

4. Задача имеет определенные степени свободы (ресурсы оптимизации), т. е. некоторые параметры функционирования системы, которые можно произвольно изменять в некоторых пределах в целях улучшения значений целевой функции.

Задачи в условиях риска. В тех случаях, когда возможные исходы можно описать с помощью некоторого вероятностного распределения, получаем задачи принятия решений в условиях риска. Для построения распределения вероятностей необходимо либо иметь в распоряжении статистические данные, либо привлекать знания экспертов. Обычно для решения задач этого типа применяются методы теории одномерной или многомерной полезности. Эти задачи занимают место на границе между задачами принятия решений в условиях определенности и неопределенности. Для решения этих задач привлекается вся доступная информация (количественная и качественная).

Задачи в условиях неопределенности. Эти задачи имеют место тогда, когда информация, необходимая для принятия решений, является неточной, неполной, неколичественной, а формальные модели исследуемой системы либо слишком сложны, либо отсутствуют. В таких случаях для решения задачи обычно привлекаются знания экспертов. В отличие от подхода, принятого в экспертных системах, для решения ЗПР знания экспертов обычно выражены в виде некоторых количественных данных, называемых предпочтениями.

Выбор и нетривиальность задач принятия решений. Следует отметить, что одним из условий существования задачи принятия решений является наличие нескольких допустимых альтернатив, из которых следует выбрать в некотором смысле лучшую. При наличии одной альтернативы, удовлетворяющей фиксированным условиям или ограничениям, задача принятия решений не имеет места.

Задача принятия решений называется тривиальной, если она характеризуется исключительно одним критерием К и всем альтернативам А_i приписаны конкретные числовые оценки в соответствии со значениями указанного критерия (рис. 1.1 а).

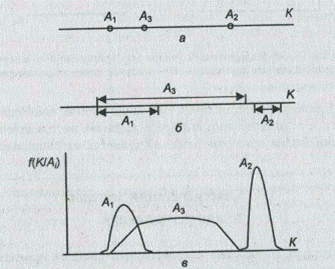
Рис. 1.1. Выбор альтернативы при одном критерии:

а — в условиях определенности; б — в условиях неопределенности;

в — в условиях риска

Задача принятия решений перестает быть тривиальной даже при одном критерии К, если каждой альтернативе А_i соответствует не точная оценка, а интервал возможных оценок (рис. 1.1 б) или распределение f(К/А_i) на значениях указанного критерия (рис. 1.1 в).

Нетривиальной считается задача при наличии нескольких критериев принятия решений (рис. 1.2) независимо от вида отображения множества альтернатив в множество критериальных оценок их последствий.

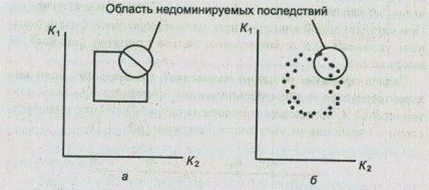
Рис. 1.2. Выбор альтернативы с учетом двух критериев: а — в случае непрерывной области альтернатив; б — в случае дискретных альтернатив

Следовательно, при наличии ситуации выбора, многокритери-альности и осуществлении выбора в условиях неопределенности или риска задача принятия решений является нетривиальной.