Обчислювальні пристрої

Найпростішою схемою є напівсуматор, який виконує операцію знаходження суми двох однорозрядних слів.

Таблиця 2.10. Таблиця 2.11.

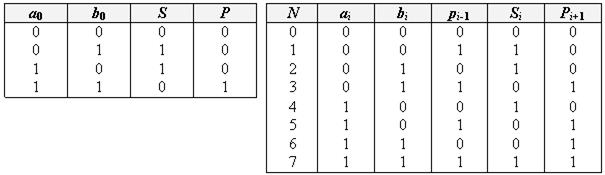
Роботу напівсуматора описує табл. 2.10, з якої знаходимо логічні рівняння для суми і для переносу:

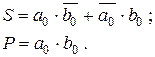
При знаходженні суми багаторозрядних слів напівсуматор може використовуватись лише в молодшому розряді. Для знаходження суми старших розрядів схема повинна мати три входи – два інформаційні і третій – вхід переносу з молодших розрядів. Схема, що відповідає цим вимогам, називається повним суматором, а логіку її роботи описує табл. 2.11.

З табл. 2.11 знаходимо наступні рівняння:

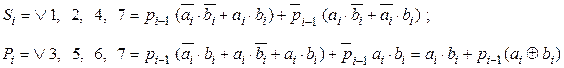
для побудови логічної схеми однорозрядного повного суматора.

Знаходження суми багаторозрядних слів може виконуватись як послідовно, так і паралельно. Для послідовного виконання операції використовується один повний суматор, загальний для всіх розрядів. Для виконання операції суми слова подаються на інформаційні розряди послідовно, починаючи з молодших розрядів (рис. 2.22).

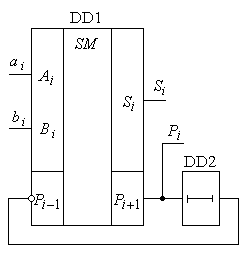Рис.2.22.

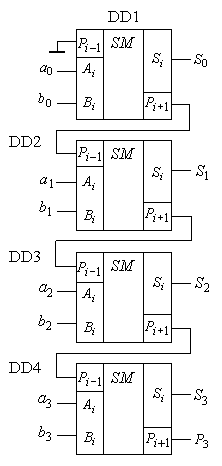Рис.2.23.

Для врахування результату операції з попереднім розрядом вхід та вихід переносу об’єднується через елемент затримки DD2. Цей елемент повинен забезпечити затримку та зберігання сигналу P_{i +1} на один такт виконання операції. Синхронно з інтервалом в один такт повинні подаватись і вхідні дані , .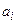

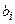Приведена схема виконання операції суми сама по собі нескладна, але вимагає складного апаратного забезпечення. До того ж, послідовне порозрядне виконання операції суттєво знижує швидкодію.

На рис. 2.23 приведена схема організації чотирьохрозрядного паралельного суматора з послідовним переносом. Для кожного розряду в ній використовуються окремі однорозрядні повні суматори, які з’єднані між собою послідовно по виходах-входах переносу. Незважаючи на паралельну одночасну подачу всіх розрядів слів, операція в і-му розряді починає виконуватись тільки після того, як поступить сигнал переносу з (і-1)-го розряду. Звідси витікає, що швидкодія суматора визначатиметься сумою затримок передачі сигналу переносу з молодшого розряду на вихід суматора старшого розряду.

Компаратори – це пристрої, що виконують порівняння двох чисел.

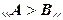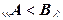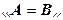Мікросхеми компараторів визначають не тільки рівність, але й нерівність двох чисел. Для цього мікросхема має три виходи: , i , на яких у залежності від співвідношення величин 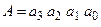, 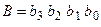з’являється активний рівень сигналу.

Логічна функція, що реалізує алгоритм роботи компаратора для одного розряду:

.

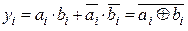(2.12)

Для багаторозрядних чисел функція (2.12) повинна виконуватись для кожного розряду. Нерівність 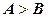має місце тоді, коли в числі А одиниці дорівнює більш старший розряд, ніж у числі В. Для чотирьохрозрядного компаратора така нерівність може бути записана у вигляді:

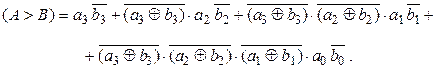
Побудова багаторозрядного компаратора можлива на базі суматора. Його реалізація можлива при виконанні операції віднімання.

Дійсно, в відповідності до законів арифметики при 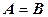на виходах всіх розрядів суматора 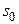, , 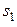, 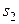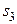буде 0 при .

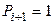При 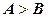значення 1 буде як на виході переносу 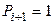, так і хоча б на одному виході 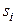. Тому ознакою 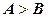може бути функція

.

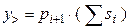При 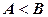результат наявності переносу .

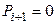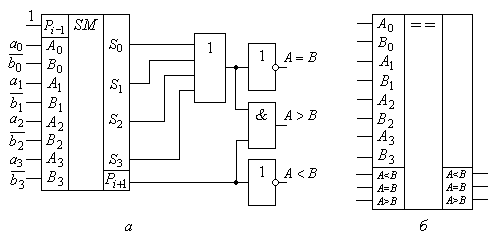
Рис.2.24.

Відповідно до сказаного, логічна схема компаратора на базі суматора К1533ИМ3 (зарубіжні аналоги – 7483PC, CDB483E, MC7483N, N7483N, SN7483AN, UCY7483N) має вигляд, приведений на рис. 2.24, а.

Компаратори широко використовуються в інформаційних системах для виділення необхідного слова в потоці цифрової інформації, для відмітки часу в часових пристроях, для виконання умовних переходів в обчислювальних пристроях. У пристроях автоматики компаратори використовуються для контролю виходу величин за межі допусків і т.п.

Арифметично-логічні пристрої (АЛП, ALU – Arithmetic-Logic Unit) – це спеціалізовані мікросхеми, які виконують арифметичні та логічні операції у відповідності до двійкового коду, який подається на керуючі входи мікросхеми. Умовне позначення АЛП в електронних схемах приведене на рис. 2.25.

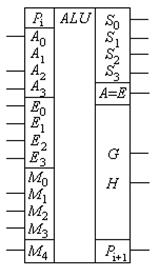
Рис.2.25.

АЛП призначений для роботи з сигналами як позитивної, так і негативної логіки, що відображається у таблиці станів мікросхеми (табл. 2.12).

У табл. 2.12 L та H позначені відповідно низький і високий рівні сигналів, незалежно від типу логіки. Знаки (+) та (–) – знаки арифметичних операцій. Результати арифметичних дій виражені в доповнюючому коді. Так як між зворотнім та доповнюючими кодами існує однозначний зв’язок, то скрізь, де вказана арифметична дія “–1”, результат на виходах зчитується у зворотному коді.

Таблиця 2.12.

Входи вибору функції	Вхід-вихід (негативна логіка)	Вхід-вихід (позитивна логіка)
М3	М2	М1	М0	Логічні функції M4 = H	Арифметичні дії M4 = L; Pi = L	Логічні функції M4 = H	Арифметичні дії M4 = L Pi = H
L	L	L	L		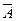A – 1		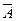A
L	L	L	H		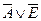AE – 1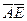
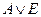
L	L	H	L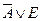
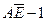
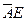
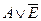
L	L	H	H	1	-1	0	-1
L	H	L	L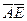
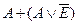
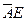
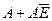
L	H	L	H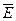
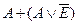
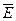
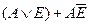
L	H	H	L		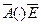A-E-1	A(+)E	A-E-1
L	H	H	H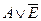
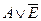
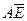
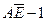
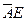
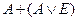
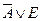
H	L	L	L				A+AE
H	L	L	H	A(+)E	A+E		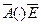A+E
H	L	H	L	E		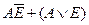E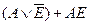
H	L	H	H		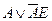AE	AE	AE-1
H	H	L	L	0	A+A	1	A+A
H	H	L	H		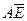AE+A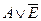
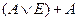
H	H	H	L	AE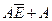
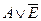
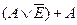
H	H	H	H	A	A	A	A-1

На відміну від суматорів, сигнал переносу на вході і виході є інверсним по відношенню до сигналів на входах А та Е. Сигнали переносу діють лише при виконанні арифметичних операцій. При використанні логічних операцій АЛП всі зазначені в табл. 2.12 функції виконує порозрядно. Функція переносу діє тільки при виконанні арифметичних дій, але в результатах цих операцій символи АЕ означають операцію І.

Якщо АЛП використовується в якості компаратора (операція 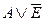), то при 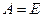на відповідному виході формується сигнал високого рівня. При 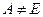відповідний сигнал формується на виході .

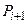Не вдаючись у подробиці роботи АЛП, слід зазначити, що в зв’язку з інтенсивним розвитком мікропроцесорної техніки розглянута схема АЛП у реальній схемотехніці майже не використовується. Її вивчення має скоріш методичне значення, адже дає можливість практично вивчати ідеологію побудови мікропрограмних автоматів і мікропроцесорів.