Особые точки и параметры задачи

Точки, в которых диаграмма нагрузка-перемещение расщепляется на две ветви, называются точками ветвления решения или точками бифуркации.

Для диаграммы, соответствующей примеру 1 (рис.2.1а), это точка .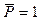

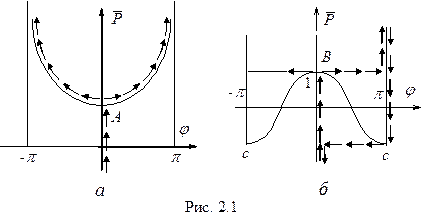
Если нагрузка достигает 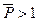, стержень вследствие всегда имеющих место случайных возмущений переходит в отклоненное положение равновесия. С ростом нагрузки отклонение нарастает, вообще говоря, плавно, но в окрестности точки бифуркации малому приращению нагрузки соответствуют достаточно большие смещения.

Иначе ведет себя система в Примере 2. При достижении значения 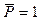(рис.2.1б) система скачком переходит в нижнее положение равновесия.

Точки, в которых положение равновесия становится неустойчивым, называются критическими, а соответствующие им значения нагрузок - критическим нагрузками. При разгрузке системы нижнее положение равновесия остается устойчивым вплоть до значения 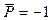, и только здесь происходит перескок. Значения` 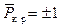принято называть верхней и нижней критическими нагрузками.

Иногда точки типа А называют критическими точками бифуркации первого типа, а точки типа В и С - второго.

Кроме точек этого типа в теории устойчивости рассматривают также особые точки, характеризующиеся тем, что в них не пересекаются два различных решения, но положение равновесия скачкообразно меняется. Такие точки принято называть предельными.

Пример 2.1

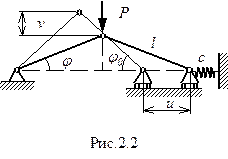
Пусть геометрия системы в ненагруженном состоянии определяется параметрами 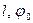(рис.2.1), а в состоянии равновесия - параметрами , 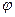а также

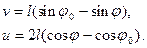
Полная энергия системы

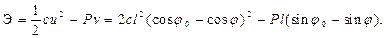
Положение равновесия определяется условием

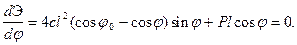(2.1)

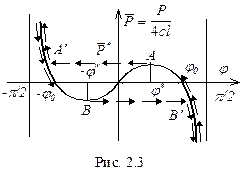
Графическая интерпретация уравнения дана на рис.2.3.

При значениях 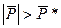система имеет одно положение равновесия, при 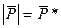- два, а при 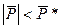- три.

Для исследования устойчивости системы в этих положениях необходимо оценить знак второй производной от энергии по параметру перемещения при 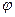, определяемых уравнением (2.I).

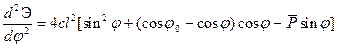(2.2)

Аналитически такой анализ довольно трудоемок, но интуитивно ясно, что состояния 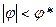неустойчивы, поскольку в этих положениях для дополнительного сжатия пружины нужно уменьшить силу 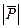.`Поэтому при увеличении силы 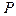система скачком переходит из точки А в точку А', а при уменьшении силы 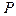- из точки В в точку В'.

Таким образом, значения ` 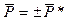определяют верхнюю и нижнюю критическую нагрузку.

Рассмотренные наипростейшие примеры не только содержат особенности, характерные для более сложных задач устойчивости стержней, пластин и оболочек. Они позволяют также в первом приближении оценить влияние отклонений от идеальной геометрии, всегда имеющие место в реальных механических системах.

Пусть в исходном ненагруженном состоянии стержни, рассмотренные в примерах 1 и 2, расположены не строго вертикально, а отклонены на некоторый малый угол 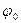(рис.2.4a) .

Это предположение равносильно тому, что сила 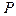прикладывается не по оси вертикально стоящего стержня, а под некоторым углом - 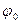( рис.2.4б) и, что существенно, не меняет этого направления в процессе отклонения системы (такую нагрузку, не меняющую ни величины, ни направления, принято называть "мертвой").

Уравнения равновесия для случаев а) и б)

(2.3)

совпадают с точностью до выбора начала отсчета. Поэтому в дальнейшем будем рассматривать только случай "а".

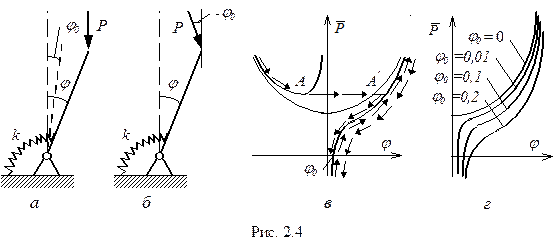
Графическая интерпретация уравнения (2.3) дана на рис.2.4 в, г. Легко видеть, что график решения при 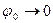асимптотически стремится к графику для идеальной системы, но при любом 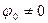, точки бифуркации отсутствуют. При нагружении система плавно отклоняется и так же плавно возвращается при снятии нагрузки. Ни при какой силе 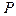система не попадает на левую ветвь, часть которой является устойчивой. Чтобы попасть на эту ветвь, систему нужно сначала отклонить на достаточно большой отрицательный угол 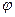и в этом положении уравновесить соответствующей силой 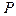. Тогда при разгрузке система скачком перейдет из точки А в А'.

На рис.2.5 дана графическая интерпретация поведения системы из Примера 1.2 с начальным отклонением .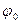

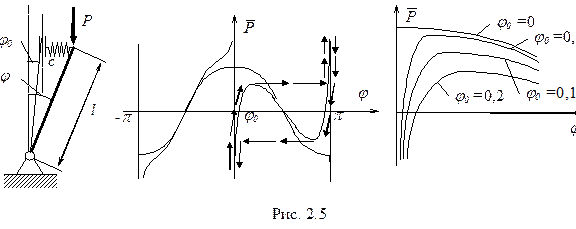
Равновесие этой системы описывается уравнением

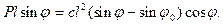
Как видно из диаграммы, точки бифуркации отсутствуют, поскольку кривые, соответствующие различным решениям, не пересекаются. Вместо них возникают предельные точки А и В, соответствующие верхнему и нижнему критическим значениям нагрузки. Причем по модулю эти значения меньше соответствующих значений для идеальной системы. Для того, чтобы попасть на левую ветвь, систему надо предварительно отклонить на отрицательный угол 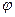. Причем тогда ни при какой силе 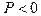или 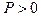перескока не произойдет.

Для более сложных систем описанные характерные особенности сохраняются.

Если идеализированная система имеет точку бифуркации первого рода, система с несовершенствами ее не имеет.

Точки бифуркации второго рода обращаются для систем с отклонениями в предельные точки, а соответствующие им критические нагрузки уменьшаются.

Линеаризованные уравнения

Для систем более сложных, чем рассмотренные, нелинейные уравнения равновесия настолько сложны, что, как правило, получить их аналитическое решение не удается. Численный же анализ, тоже весьма трудоемкий и сложный, не дает возможности провести качественный анализ поведения систем, подобных рассматриваемой, поскольку проводится для конкретных геометрических и жесткостных параметров системы.

Поскольку потеря статической устойчивости для большинства конструкций недопустима, нас всегда интересует не столько поведение системы в закритическом состоянии (после потери устойчивости), сколько сами критические точки и соответствующие им критические нагрузки. Их удается найти с помощью приближенных линеаризованных уравнений.

Логика рассуждений такова: раз точки бифуркации это точки пересечения различных ветвей решения, то для их отыскания достаточно установить наличие форм равновесия, смежных с исходной. Это позволяет ограничиться рассмотрением равновесия систем при малых параметрах отклонения от исходной формы равновесия. В уже рассмотренных нами примерах таким малым параметром оказывается угол 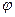. Разложив в ряд Тейлора тригонометрические функции этого угла, мы можем ограничиться первыми членами разложений

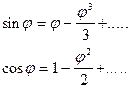(2.4)

Обратимся снова к Примеру 1.1. Линеаризуем уравнение (1.2), т.е. удержим в разложении (2.4) для 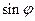только первый линейный член.

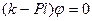. (2.5)

Из (2.5) получаем исходную форму равновесия 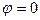. Кроме этого решения, справедливого при любом параметре 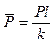, уравнение (2.5) при 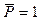имеет решение 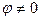, т.е. 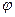- любое, но, разумеется, малое.

Таким образом, мы определили ` .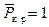

Уравнение равновесия (1.3) для Примера 1.2 в результате линеаризации принимает вид

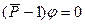(2.6)

и определяет исходную форму равновесия 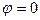и возможность нетривиального решения 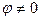при ` .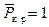

Мы снова нашли точку бифуркации и критическую нагрузку, в данном случае - верхнюю. Естественно, что ограничившись 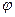, близкими к нулю, мы не смогли найти точку бифуркации, соответствующую 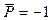. Такую точку легко найти, исследуя возможность равновесия в положении, близком к очевидному равновесию при 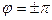. Для этого 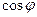надо разложить в окрестности p , записав

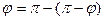
и приняв 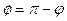малым, т.е.

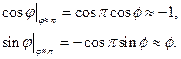
Тогда уравнение (1. 3) примет вид

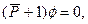
откуда и находим нижнюю критического нагрузку .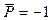

Линеаризованные уравнения позволяют найти точки бифуркации в заранее известных положениях равновесия, но не дают информации ни о характере этих точек, ни о поведении системы в закритическом состоянии, т.е. при больших отклонениях. Поэтому найти с их помощью предельные точки, в которых нет ветвления форм равновесия, строго говоря, невозможно. Однако, и в этих случаях они могут оказаться полезными.

Например, если в Примере1.3 угол 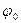мал настолько, что допустимо принять

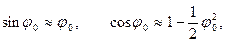
то это тем более допустимо для функций угла 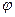. Тогда вместо (2.I) можно рассматривать приближенное выражение

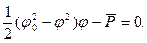(2.7)

Это уравнение нельзя назвать линеаризованным, поскольку мы удержали и вторые члены разложения (2.4) . Однако анализировать его значительно легче, чем (2.1). При сделанных допущениях вместо (2.2) имеем

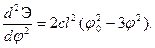
Легко видеть, что эта величина меняет знак при

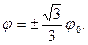(2.8)

Подставив (2.8) в (2.7), находим приближенные значения критических нагрузок в этих предельных точках.

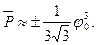
Исследуем с помощью линеаризованных уравнений систему не с одной, а с двумя степенями свободы.

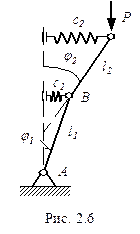
Пример 2.2

Уравнения равновесия такой cистемы:

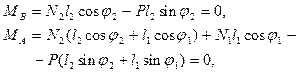(2.9)

где усилия в пружинах:

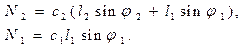(2.10)

Система (2.9) после подстановки в нее (2.10) и линеаризации примет вид

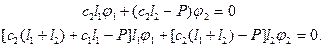(2.11)

Кроме тривиального 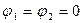решения , соответствующего вертикальному положению равновесия стержней, система может иметь и нетривиальные решения 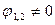, если ее определитель:

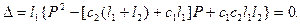(2.12)

Корни уравнения (2.12) дают два значения нагрузки (две точки бифуркации). Пусть для конкретности .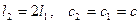

Тогда корни уравнения (2.12)

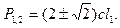(2.13)

При найденных значениях нагрузки (2.13) уравнения (2.11) совпадают, что позволяет найти лишь соотношения между значениям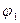и и .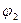

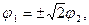(2.14)

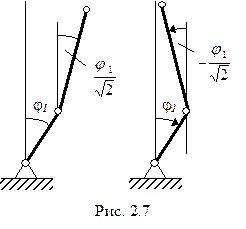
которым соответствуют две формы равновесия, найденные с точностью до множителя (рис. 2.7).

Рассмотренный пример позволяет сделать следующие заключения, характерные для всех задач статической устойчивости.

1. Точки бифуркации находятся из условия нетривиальности решения и математически являются собственными значениями задачи.

2. Количество точек бифуркации совпадает с числом степеней свободы системы, если характеристическое уравнение не имеет кратных корней.

3. Формы отклоненного равновесия математически являются собственными функциями задачи и определяются с точностью до амплитуды.