Задачи теории информации

Теория информации изучает способы наилучшей передачи сообще­ний по каналам передачи информации с заданными свойствами. Задача выбора наилучшего способа передачи (извлечения) сообще­ний является основной задачей не только теории информации, но и инженерной практики на этапе эксплуатации систем связи.

Для решения основной задачи теории информации необходимо в первую очередь решить задачу согласования информационных характеристик источника информации (сообщений) и канала связи, которая требует решения ряда частных задач:

- определения количества информации, содержащегося в сообщении;

- оценки информативности источника информации (сообщений) в целом;

- определения скорости передачи информации, с которой она может быть передана по заданному каналу;

- определения количества информации, теряемой в канале в результате воздействия помех.

Информацию для передачи, хранения, обработки или распространения необходимо представить в виде каких-либо символов (знаков) x_k, k 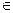[1, L]. Эти символы (знаки) x_k называются элементарными символами источника сообщений.

Множество различных элементарных символов источника сообщений (ИС) {x_k}, k = [1, L], используемых источником информации (ИИ) для формирования сообщений, называется алфавитом источника сообщений, а мощность этого множества L – объемом алфавита.

Упорядоченная совокупность элементарных символов x_k, отображающих информацию,образует сообщение {x}.

Для решения основной и частных задач теории информации необходимо в первую очередь определить меру количества информации.

В 1946 г. К. Шеннон[2] предложил связать количество информации, содержащееся в сообщении, с вероятностями использования символов алфавита ИС при формировании сообщений. Такой подход для количественной оценки информации был принят и назван интуи­тивно-вероятностным подходом [2 – 5].

Прежде всего, заметим, что сообщение об известном событии не содержит информации, так как для получателя в нем нет ничего но­вого. С другой стороны, можно считать, что маловероятное сообще­ние (сенсация) содержит много информации, так как оно является неожиданным и может существенно повлиять на дальнейшие действия получателя информации.

Отсюда логично предположить, что количество информации, содержащееся в k-м символе алфавита ИС x_k, находится в обратной за­висимости от вероятности его появления Р(x_k).

В теории информации, как правило, количество информации, содержащееся в символах любого алфавита, измеряют в битах, т.е. бит является единицей количества информации: 1 бит ин­формации содержит символ сообщения, вероятность появления которого равна 1/2.

Контрольные вопросы

1. Что подразумевается под термином «сообщение»?

2. Какая взаимосвязь между информацией и сообщением?

3. Что такое алфавит источника сообщений?

4. Понятия «источник информации» и «источник сообщений».

5. Поясните, что такое бит.