Числовые последовательности. Примеры
Рассмотрим функции 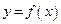 , заданные на множестве натуральных чисел
, заданные на множестве натуральных чисел 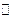 . Такие функции называются функциями натурального аргумента.
. Такие функции называются функциями натурального аргумента.
Множество значений функции натурального аргумента – 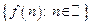 называется числовой последовательностью (или последовательностью), а каждое значение
называется числовой последовательностью (или последовательностью), а каждое значение 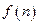 этой функций – членом
этой функций – членом
числовой последовательности. Так как числовая последовательность является конкретным и часто используемым понятием, то удобно для неё использовать иное обозначение, а именно, вместо 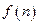 будем писать
будем писать 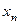 :
: 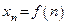 .
.
Члены числовой последовательности располагаются в порядке возрастания аргумента
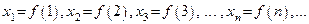 ,
,
при этом
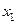 – первый член последовательности;
– первый член последовательности;
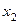 – второй член последовательности;
– второй член последовательности;
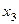 – третий член последовательности;
– третий член последовательности;
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
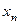 –
– 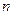 -й или общий член последовательности.
-й или общий член последовательности.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Последовательность 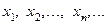 коротко можно обозначать
коротко можно обозначать  .
.
Последовательность 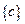 , где
, где 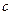 произвольное вещественное число, называется стационарной последовательностью или постоянной величиной.
произвольное вещественное число, называется стационарной последовательностью или постоянной величиной.
Пусть  – произвольная последовательность. Для всякой последовательности натуральных чисел
– произвольная последовательность. Для всякой последовательности натуральных чисел 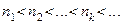 последовательность
последовательность 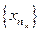 называется подпоследовательностью последовательности
называется подпоследовательностью последовательности  .
.
Пример 1.1. 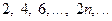 или
или 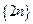 .
.
Пример 1.2. 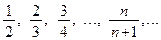 или
или 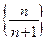 .
.
Пример 1.3. 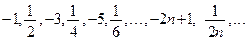 или
или 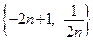 .
.
Пример 1.4. 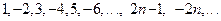
или 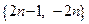 .
.
Пример 1.5. 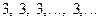 или
или 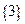 .
.
Дата добавления: 2016-09-06; просмотров: 2414;










