Указание по чередованию

Указания, представленные в Уроках 10..15, рассматриваются и проиллюстрированы в среде бычьего рынка. Кроме специально оговоренных случаев, они применяются в равной степени и в среде медвежьего рынка, в контексте которого иллюстрации и выводы следует инвертировать.

Чередование

Указание по чередованию является весьма широким в своем применении и предупреждает аналитика всегда предполагать некоторое отличие в следующем проявлении подобной волны. Гамильтон Болтон (Hamilton Bolton) сказал:

Хотя чередование не говорит точно, что произойдет, оно дает ценное предупреждение о том, чего не следует ожидать и, следовательно, его полезно помнить при анализе волновой структуры и оценке будущих возможностей. Главным образом, оно обучает аналитика не предполагать, что раз уж последний рыночный цикл вел себя определенным образом, следующий, несомненно, должен быть именно таким (что большинство людей и склонны делать). Поскольку "упрямцы" никогда на прекращают поучать, то тот день, в который большинство инвесторов "уловят" видимую закономерность рынка, станет днем, когда рынок изменит ее на совершенно другую. Тем не менее, Эллиотт пошел дальше в утверждении, что чередование фактически является законом рынка.

Чередование внутри импульсных волн

Если волна 2 импульса является резкой коррекцией, то предполагается, что волна 4 будет боковой коррекцией и наоборот. Рис. 2-1 показывает наиболее характерные структуры в импульсных волнах, направленных и вверх, и вниз, как рекомендует указание по чередованию. Резкие коррекции никогда не содержат в себе нового ценового экстремума, т.е. такого значения цены, которое лежит за пределом ортодоксального окончания предыдущей импульсной волны. Они почти всегда являются зигзагами (одиночными, двойными или тройными); иногда они являются двойными тройками, которые начинаются зигзагом. Боковые коррекции включают в себя волновые плоскости, горизонтальные треугольники, двойные и тройные коррекции (волновые комбинации*). Обычно они содержат новый ценовой экстремум, т.е. такое значение цены, которое лежит за пределами ортодоксального окончания предыдущей импульсной волны. В редких случаях стандартный треугольник (тот, который не содержит ценового экстремума) в четвертой волновой позиции заменит резкую коррекцию, чередуясь с другим типом боковой модели во второй волновой позиции. Идея чередования внутри импульсных волн может быть подытожена следующим образом: **один из двух корректирующих процессов будет содержать движение к окончанию предыдущего импульса (импульсной подволны*) или за его пределы, а другой - нет**.

Диагональные треугольники не демонстрируют чередования между волнами 2 и 4. Обычно, обе они являются зигзагами. Волновые удлинения являются выражением чередования, поскольку движущие волны чередуются по длине. Обычно, первая волна - короткая, третья - удлиненная и пятая - вновь короткая. Волновые удлинения, которые обычно происходят в волне 3, иногда проявляются в волне 1 или 5, это - еще одно проявление чередования.

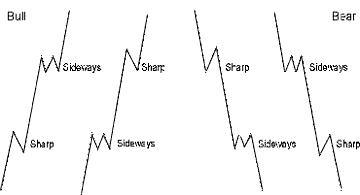
Рисунок 2-1

Чередование внутри корректирующих волн

Если большая коррекция начинается с волновой плоскости а-b-с в качестве волны А, то в качестве волны В ожидается зигзаг a-b-c (рис. 2-2) и наоборот (см. рис. 2-3). Даже навскидку видно, что подобное сочетание весьма практично, поскольку первый рисунок отражает уклон вверх в обоих подволнах (из-за мощной предыдущей движущей волны*), в то время как второй - уклон вниз.

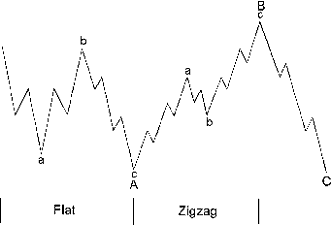
Рисунок 2-2

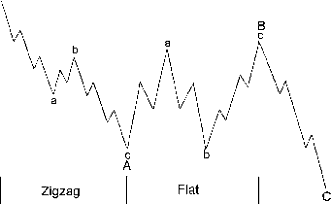
Рисунок 2-3

Достаточно часто бывает так, что если большая коррекция начинается с простого зигзага a-b-c в качестве волны А, то волна В раскрывается в более замысловатый зигзаг a-b-c чтобы достичь некоторого типа чередования, как на рис. 2-4. А волна С иногда бывает еще более сложной, как на рис. 2-5. Обратный порядок сложности (подволн*) менее распространен (например, рис. 2-16, Урок 15, волна 4 *).

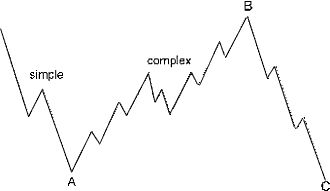
Рисунок 2-4

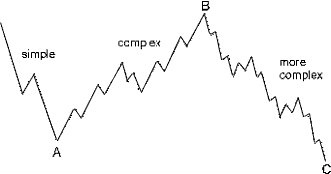
Рисунок 2-5