Углеводородных газов

Как отмечалось выше, в нефтяной газ при нормальных и стандартных условиях входят углеводороды от С₁ до С₄: метан, этан, пропан, изобутан и н-бутан.

С точки зрения строения все они линейно построены, а потому это, так называемые, неполярные углеводороды.

С точки зрения химии, если в системе силами взаимодействия между молекулами можно пренебречь, то такую систему можно рассматривать как идеальную.

К газообразным углеводородам с точки зрения физикиможно применять законы для идеальных систем.

С точки зрения термодинамики идеальным называется газ, внутренняя энергия которого зависит только от температуры и для которого справедливы равенства:

(∂Е/∂V)_T = 0, z = Р·V/Q·R·T = 1, (2.4)

где Е – внутренняя энергия парообразования, Дж/моль;

z – коэффициент, характеризующий степень отклонения реального газа от закона идеального газа.

С точки зрения математики к расчёту физико-химических свойств газа, как многокомпонентной смеси можно применять принцип аддитивности.

Аддитивный подход к расчёту физико-химических и технологических параметров означает, что каждый компонент газа в смеси ведёт себя так, как если бы он в данной смеси был один.

Следовательно, для оценки макроскопических свойств нефтяного газа (при н.у. и с.у.) применимы аддитивные методы расчётов физико-химических и технологических параметров (П_смеси):

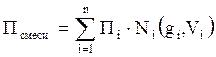, (2.5)

где N_i – мольная доля;

g_i – весовая доля;

V_i – объёмная доля;

П_i – физико-химическое свойство i-го компонента.

Для идеальных газов общее давление в системе (смеси газов) равно сумме парциальных давлений компонентов (закон Дальтона):

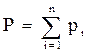, (2.6)

где Р – общее давление смеси газов;

р_i – парциальное давление i-го компонента в смеси.

Откуда

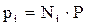, (2.7)

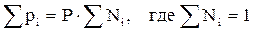. (2.8)

То есть, парциальное давление компонента в газовой смеси равно произведению его молярной доли на общее давление смеси газов.

Аддитивность парциальных объёмов (V_i) компонентов газовой смеси выражается законом Амага:

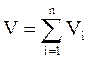, (2.9)

где V – общий объём смеси газов;

V_i – мольный объём i-го компонента газа в смеси.

По аналогии с уравнениями (2.7–2.8) мольный объём компонента в газе можно оценить:

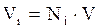. (2.10)

Как аддитивные величины рассчитывают все физико-химические свойства газа, например, плотностьсмеси газов:

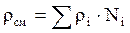, (2.11)

где ρ_i – плотность i–го компонента;

N_i – мольная доля i–го компонента.

Молекулярная масса смеси газовых компонентов рассчитывается по принципу аддитивности по выражению (2.12, левое выражение) для смесей, состав которых выражен в мольных или объёмных долях. Для смесей, состав которых выражен в массовых процентах по (2.12, правое выражение):

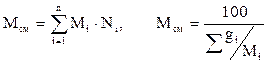[u2] . (2.12)

Рассмотрим пример. При приготовлении рекомбинированной пробы смешивают следующие объёмы (V) газов: 100 м³ пропана (C₃H₈), 75 м³ изобутана (i-С₄Н₁₀) и 75 м³ нормального бутана (n-С₄Н₁₀).

Дано: V_i, м³ M_i, г/моль

C₃H₈ 100 44

i-C₄H₁₀ 75 58

n-C₄H₁₀ 75 58

Найти: чему равна молекулярная масса смеси газов (М_см)?

Решение. Находим общий объём газовой смеси 100 + 75 + 75 = 250 (м³), и рассчитываем её объёмный состав в процентах:

250 м³ – 100 %,

100 м³ – Х %;

Х = 100·100/250 = 40 (%) или V_{C3H8 =} 0,4 (в долях);

Аналогично, для → i-C₄H₁₀ – X % Þ

X = 75·100/250 = V_i-C4H10 = 30 % = 0,3 (в долях);

для → n-C₄H₁₀ – 30 % Þ V_n-C4H10 = 30 % = 0,3 (в долях).

Зная молекулярные массы газовых компонентов смеси (C₃H₈ → 44; C₄H₁₀ → 56) и, что V_i = N_i, рассчитываем величину молекулярной массы смеси газа (M_см):

M_см = SM_i·N_i = 44·0,4 + 58·0,3 + 58·0,3 = 17,6 + 17,4·2 = 52,4 (г/моль).