Оценка математического ожидания

Проверка состоятельности. Согласно закону больших чисел (теорема Чебышева) [13], при неограниченном увеличении числа независимых испытаний среднее арифметическое наблюдаемых значений случайной величины, имеющей конечную дисперсию, сходится по вероятности к ее математическому ожиданию, т. е.

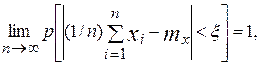(5.5)

где ξ - сколь угодно малое положительное число.

Нетрудно заметить, что вместе с выполнением равенства (5.5) выполняется и условие состоятельности (5.2).

Проверка несмещенности.Пусть имеется l периодов наблюдений (l →∞) продолжительностью п лет. Найдем математическое ожи­дание оценок математического ожидания методом моментов

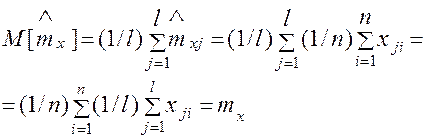
Таким образом, 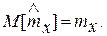Отсюда, согласно выражению (5.1), оценка математического ожидания методом моментов является несмещенной.

Оценка дисперсии

Проверка состоятельности. Раскроем квадрат в числителе формулы (3.37). Тогда

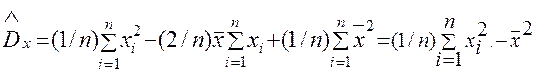
Сумма 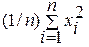представляет собой среднее арифметическое п наблюденных значений случайной величины X², или, иначе, оценку математического ожидания X² методом моментов 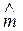_x². Как показано выше, эта оценка сходится по вероятности к m_x² В свою очередь 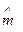_x сходится по вероятности к т_х и тогда вся правая часть полученного равенства сходится по вероятности к

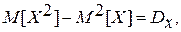
где 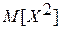- начальный момент второго порядка [см. формулу (3.22)].

Следовательно, эмпирическая оценка дисперсии D_x методом моментов является состоятельной.

Проверка несмещенности. Преобразуем формулу оценки дисперсии (3.37), отняв и прибавив в скобках математическое ожидание

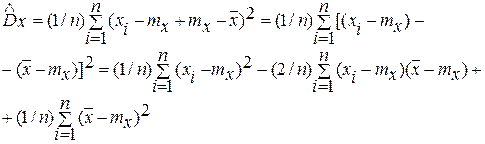
и найдем математическое ожидание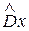

В полученном выражении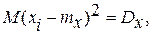

В свою очередь (см. раздел 3.1.5), согласно свойств числовых характеристик 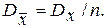Тогда

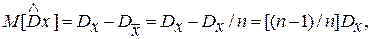
т.е.

(5.6)

Таким образом, оценка дисперсии имеет отрицательную смещенность, равную в среднем D_x/n. Для ее учета следует правую часть формулы (3/37) умножить на п/(п— 1). В ре­зультате получаем

(5.7)

В соответствии с этим для оценки среднего квадратического отклонения должна использоваться формула

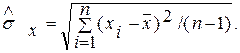(5. 8)

а для оценки коэффициента вариации

(5.9)

Для определения коэффициента асимметрии на основании аналогичных выводов получена формула

(5.10)

Следует отметить, что при п ≥30 во многих расчетах с достаточной точностью можно принимать в знамена­теле формул (5.7) —(5.10) не п— 1, а п.

Практически на всех языках программирования имеются па­кеты программ для оценки числовых характеристик методом мо­ментов на ЭВМ.