Оценка параметров законов распределения в геоэкологических исследованиях

Имеется случайная величина X, закон распределения которой содержит неизвестный параметр a. Требуется на основании опытных данных найти подходящую оценку этого параметра.

Представим себе, что в нашем распоряжении имеется ряд наблюдений бесконечной продолжительности x₁, х₂, . .., x_N (N→∞). Этот ряд наблюдений может рассматриваться как генеральная совокупность значений исследуемого процесса X. Разобьем генеральную совокупность на l частных выборок (l→∞) объемом в п (n<<N) членов каждая. Пронумеруем значения X в соответствии с поряд­ковым номером выборки j и порядковым номером значений X в данной выборке —i.

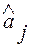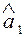По материалам наблюдений, представленным в первой выборке x₁₁, х₁₂,..., x_1п, рассчитано значение параметра а. Это значение называется ста­тистической или выборочной (вычислено по выборке) оценкой параметра а.Обозначим эту оценку через , где j – номер выборки. Есте­ственно, что значение является функцией входящих в первую выборку значений, т. е. = f(x₁₁, х₁₂, . .., x_1п). Аналогично 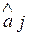является функцией значений, входящих в J – ую выборку, то есть 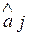= f(x_j1, х_j2, . .., x_jп) и т.д.

Значения случайнойвеличины, очевидно, могут быть разными в разныхвыборках, и появление именно их в данной выборке совершенно случайно. Отсюда следует, что 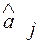, являющееся функцией входящих в выборку значений x_ji , также явля­ется значением случайной величины, имеющей, как и каждая случайная величина, свой закон распределения F_a. Этот закон рас­пределения разный для различных параметров распределения и, при прочих равных условиях, зависит также от закона распределения случайной величины X и от объема выборки.

Таким образом, по каждой из l выборок может быть получена своя оценка данного конкретного параметра а. Представим эти оценки в виде кривой распределения эмпирических значений или оценок а (рис. 5.1).

Рис.5.1. Кривые распределения оценок статистического параметра.

1 – n=N; 2 – n₂<n₁; 3 – n₃<n₂; 4 – n₄<n₃

Будем теперь увеличивать объем выборок п. В этом случае кривая распределения 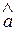будет сужаться по оси абсцисс, т. е. рассеивание выборочных оценок относительно действитель­ного значения будет в соответствии с законом больших чисел [ 13 ] уменьшаться, и при n→∞, с вероятностью p → 1, 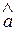должно быть равно а, т. е. кривая распределения должна превра­титься в линию, проходящую через ось абсцисс в точке 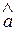=a, равную по оси ординат 1.

Из приведенных графиков распределения оценок а при различных n видно, что при малых значениях n выборочные оценки а могут весьма существенно отличаться от действительных. Очевидно, что, чем меньше, при прочих равных условиях, отличие выборочных оценок от действительных и чем меньше вероятность больших отличий, тем лучше оценка.

Точно так же ряды данных наблюдений, используемые в науках о Земле, являются выборками из генеральной совокупности и рассчитанные по ним значения числовых характеристик (оценки), как правило, отличаются от действительных.

Принятые оценки параметров распределения, по-видимому, должны наилучшим образом отражать их действительные значе­ния. При этом, исходя из приведенных выше рассуждений, каждая оценка параметра является функцией выборки и ее следует считать наблюденным значением некоторой случайной величины. Следовательно, о качестве оценки параметра распределения с помощью данной статистики необходимо судить не по индивидуальным значениям этой статистики, а по ее выборочному распределению.

Исходя из этого, рассмотрим основные требования к выборочным оценкам.

Для того, чтобы какая-то статистическая оценка 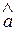(x₁, х₂, ..., x_п) имела наибольшую практическую ценность, она должна удовлетворять следующим требованиям.

1. Быть несмещенной.

Несмещенными называются оценки, математическое ожидание которых равно оцениваемому параметру, т. е.

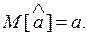(5.1)

Это означает, что центр распределения оценок числовой харак­теристики по множеству выборок (см. рис. 5.1) должен совпадать с действительным значением этой характеристики.

Естественно, что в качестве приближения неизвестного пара­метра лучше брать несмещенные оценки, чтобы не делать систе­матических погрешностей в сторону завышения или занижения.

Бывают случаи, когда возникает необходимость использовать смещенные оценки. Тогда, если 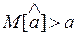оценка называется по­ложительно смещенной, а если 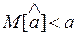— отрицательно сме­щенной.

2. Оценка должна быть состоятельной.│

Оценка 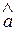называется состоятельной, если она сходится по ве­роятности к оцениваемому параметру при неограниченном возра­стании числа опытов, т. е.

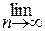
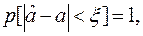(5.2)

где ξ— сколь угодно малое положительное число.

Для выполнения этого требования достаточно, чтобы дисперсия оценки при увеличении п стремилась к нулю, т. е.

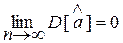(5.3)

и, кроме того, чтобы оценка была несмещенной.

Требование состоятельности практически означает, что с увеличением объема выборок рассеивание оценок относительно ма­тематического ожидания (см. рис. 5.1), совпадающего с действительным значением числовой характеристики, должно уменьшаться и при достаточно большом п отклонение 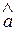от а с р→ 1 должно быть меньше любого наперед заданного значения.

Желательно, чтобы этому требованию удовлетворяла всякая оценка, пригодная для практического использования.

3. Оценка числовой характеристики распределения должна быть эффективной.

Оценки, обладающие свойством несмещенности и состоятельности, при ограниченном числе опытов могут иметь разные дисперсии. Очевидно, что, чем меньше дисперсия оценки, т. е. чем меньше разброс относительно действительного значения (см. рис. 5.1), тем меньше вероятность грубой погрешности при определении приближенного значения параметра.

Оценка, обладающая свойством

(5.4)

называется эффективной.