МАТРИЦЫ НА МНОЖИТЕЛИ. СХЕМА ХАЛЕЦКОГО

Мы видели, что прямой ход метода Гаусса преобразует СЛАУ Ax=b в Ux=j, где

j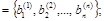

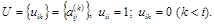
Найдем связь между компонентами векторов b и j. Для этого обратимся к уравнениям (4.3):

при k=1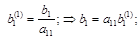

при k=2

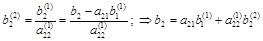и т.д.

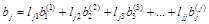, j=1…n,

где .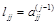

Таким образом, получили систему уравнений вида b=Lj, где L – нижняя треугольная матрица.

Перепишем эту систему в виде j=L^–1b, тогда Ux= L^–1b или

LUx= b.

Сравнивая с исходным уравнением, получаем A=LU, или в координатном виде

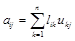, (4.4)

то есть матрица А представлена в виде произведения двух треугольных матриц: нижней треугольной матрицы с ненулевыми диагональными элементами и верхней треугольной матрицы с единичной главной диагональю (LU – разложение).

Существует теорема об LU–разложении [6].

Если все угловые миноры матрицы А отличны от нуля, то матрицу А можно единственным образом представить в виде LU – разложения, т.е. произведения A=LU.

Следствие. Метод Гаусса можно применять тогда и только тогда, когда угловые миноры матрицы отличны от нуля.

Получим формулы для определения элементов этих треугольных матриц.

Для этого преобразуем правую часть формулы (4.4) двумя способами.

1. .

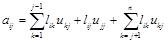Так как 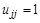, а последняя сумма равна нулю ( 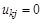при j<k), то

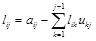при i ³ j. (4.5)

Имеем рекуррентную формулу для нахождения коэффициентов нижней треугольной матрицы. Здесь l₁₁=a₁₁ , u₁₁=1.

2. .

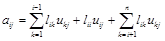Так как последняя сумма равна нулю ( 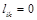при k> i), то

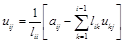при i < j . (4.6)

Имеем рекуррентную формулу для нахождения коэффициентов верхней треугольной матрицы. Обратите внимание на то, что эта формула работает в связке с формулой (4.5).

Таким образом, матрицы разложения определены формулами (4.5–4.6).

Но не забываем, что наша конечная цель – решение уравнения Ах=b. Поэтому назовем разложение матрицы на множители первым этапомпоиска решения.

Второй этап – решение уравнения Lj=b. Найти вектор j довольно просто, так как L – треугольная матрица:

.

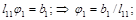
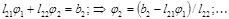
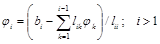Третий этап – решение уравнения Ux=j. Так как U – тоже треугольная матрица, то

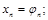
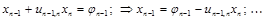
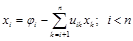
Этот процесс носит название схемы Халецкого (Cholesky). Она весьма экономна, когда надо найти решение систем линейных алгебраических уравнений с постоянной матрицей А и переменным вектором правых частей b.