Квантильные оценки случайных погрешностей измерительных
Основные понятия и классификация погрешностей
Одной из основных характеристик измерительных приборов и систем является точность, которая определяет степень совершенства и качество их работы. Более широкое использование получила характеристика противоположная точности – погрешность.
В общем случае результат x(t) любого измерения отличается от истинного значения xи(t) измеряемой величины на величину погрешности измерения
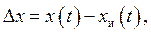 (2.1)
(2.1)
которая зависит от точности используемого метода и средства измерения, квалификации оператора и условий, при которых производится измерение.
Погрешностью Δy измерительного прибора, системы и иного средства измерения называется разность между значением y(t) измеренного параметра (показанием прибора, системы) и значением параметра, измеренным идеальным измерительным прибором, системой (истинным значением) yи(t), т.е.
Δy= y(t) – yи(t). (2.2)
Следовательно, погрешность измерительного прибора, системы и иного измерительного устройства принадлежит данному средству измерения и может быть определена при испытаниях и занесена в его паспорт.
Погрешности измерительных приборов и систем классифицируют по следующим признакам [6, 9]:
Классификация погрешностей по размерности
В зависимости от размерности различают: абсолютные погрешности, относительные погрешности, приведенные относительные погрешности.
Абсолютные погрешности измерительных приборов, систем и других измерительных устройств (ИУ) выражаются в единицах измеряемой величины и равна разности между его показанием x и действительным (истинным) значением измеряемой величины xи
Δx=x – xи.
Абсолютная погрешность ИУ в единицах выходного сигнала (приведенная к выходу ИУ)
Δy=y – yи,
где y – фактический выходной сигнал; yи – идеальный выходной сигнал, т. е. значение выходного сигнала, отвечающее действительному (истинному) значению измеряемой величины в соответствии с заданной статической характеристикой.
Рассматривая малое приращение сигнала Δy как дифференциал функции y=f(x), можно получить приближенную связь между погрешностями Δx и Δy:
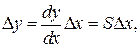 (2.3)
(2.3)
где S – чувствительность ИУ.
Относительная погрешность ИУ равна отношению абсолютной погрешности Δx и Δy к текущему значению соответствующей величины x и y:
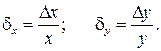 (2.4)
(2.4)
Если характеристика прибора линейна и проходит через начало координат (y=S× x), то
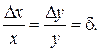 (2.5)
(2.5)
Приведенная относительная погрешность ИУ равна отношению абсолютной погрешности Δx или Δy к соответствующей абсолютной величине диапазона измерения xд или yд:
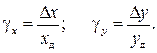 (2.6)
(2.6)
Если характеристика ИУ линейна (y= A+ Sx), то
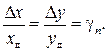
Наибольшая приведенная относительная погрешность, выраженная в процентах называется классом точности измерительного прибора (системы) K, т. е.
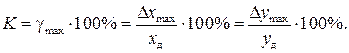 (2.7)
(2.7)
Классификация погрешностей по характеру связи между величиной погрешности и уровнем сигнала
В зависимости от характера связи между величиной погрешности и уровнем измеряемого сигнала различают аддитивные погрешности, мультипликативные погрешности, степенные погрешности (квадратические, кубические и т. д.), периодические погрешности.
Погрешности называют аддитивными (рис. 2.1, а), если их значения не зависят от уровня измеряемых сигналов, т. е. Δy=a.
Погрешность называется мультипликативной (рис. 2.1, б), если ее значение пропорционально измеряемой величине, т. е. Δy=bx, где b – постоянный коэффициент.
Степенная погрешность пропорциональна xm. Если m=2, то погрешность будет квадратической, т. е. Δy=cx2. Если m=3, то погрешность будет кубической, т. е. Δy=dx3.
Периодическая погрешность (рис. 2.1, в) изменяется в зависимости от измерямой величины x по периодическому закону, например
Δy=A sin kx.
В общем случае погрешность измерительного прибора (системы) может содержать несколько составляющих
Δy= a + bx + cx2 + dx3 +… (2.8)
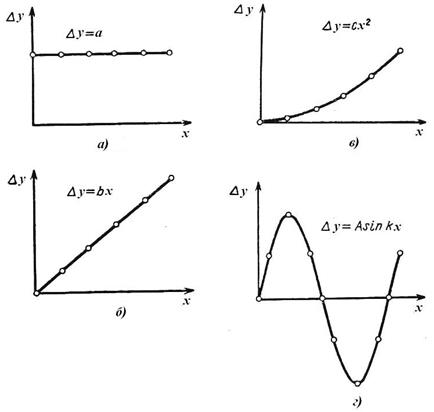
Рис. 2.1. Графики погрешностей измерительных приборов и систем:
а) аддитивная погрешность; б) мультипликативная погрешность;
в) степенная погрешность; г) периодическая погрешность.
Классификация погрешностей по закономерности их появления при многократных измерениях
Если в основу классификации положить повторяемость погрешностей при многократных измерениях, то все погрешности можно разделить на систематические и случайные.
Систематические погрешности имеют определенное значение в каждой точке характеристики измерительного прибора или системы и при многократных измерениях в одинаковых условиях закономерно повторяются. Они вызываются несовершенством методов измерения и схем конструкций приборов. Влияние систематических погрешностей может быть заранее установлено и учтено. В современных приборах и системах систематические погрешности компенсируются при помощи специальных устройств или учитываются при обработке результатов измерений.
Случайные погрешности – это погрешности, имеющие рассеяние по величине и знаку при многократных испытаниях (измерениях) в одних и тех же условиях, причем появление тех или иных значений случайных погрешностей при единичных замерах незакономерно.
Возникновение случайных погрешностей обусловлено случайными изменениями параметров в уравнениях измерения, случайными изменениями параметров схем и конструкций приборов и систем, влиянием внешних случайных возмущений и т. д. В общем случае случайные погрешности могут содержать систематическую составляющую.
Классификация погрешностей по причинам их появления
В зависимости от причин, порождающих погрешности, различают методические и инструментальные погрешности.
Методические погрешности возникают из-за несовершенства метода измерения, т. е. неоднозначной связи между измеряемой величиной и величиной, воспринимаемой чувствительным элементом прибора или системы, а также из-за приближений, допускаемых при проектировании прибора или системы. Методические погрешности характерны, в частности, для приборов и систем, принцип действия которых основан на косвенных методах измерения. Например, градуировочная формула барометрического высотомера, выражающая зависимость атмосферного давления p от высоты H, в диапазоне высот от 0 до 11 км имеет вид [9]
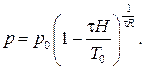
где R – универсальная газовая постоянная; τ – высотный градиент температуры.
Входящие в эту формулу параметры в соответствии со стандартной атмосферой СА-73, принимаются равными некоторым постоянным значениям: р0=760 мм рт.ст.; T0=288,16 K; R=29,27м/град; τ=0,0065 град/м. При реальных измерениях эти параметры могут отличаться от принятых значений, что и приводит к методическим погрешностям.
Методические погрешности не зависят от качества изготовления прибора или системы, они одинаковы для всех образцов данного типа.
Инструментальные погрешности возникают, во-первых, из-за несовершенства технологического процесса изготовления прибора или системы, во-вторых, в следствии изменения геометрических размеров и физических характеристик деталей и узлов прибора (системы) при изменении окружающих условий и, в третьих, из-за изменения характеристик прибора или системы при изменении режимов питания, влияния внешних возмущений на параметры прибора или системы.
Классификация погрешностей по характеру изменения во времени
По данному признаку погрешности измерительных приборов и систем можно разделить на статические и динамические.
Статические погрешности Δyст возникают при установившемся режиме измерения, когда измеряемая величина x и выходной сигнал y сохраняют постоянное значение.
Динамические погрешности Δyдин имеют место при неустановившемся режиме измерения. Под динамической погрешностью понимают ту часть погрешности, которая добавляется к статической погрешности в неустановившемся режиме измерения и является функцией времени.
Следовательно, общая погрешность прибора в неустановившемся режиме измерения равна сумме статической и динамической погрешностей
Δy(t)= Δyст + Δyдин(t). (2.9)
Классификация погрешностей в зависимости от условий работы
прибора или системы
Практика технических измерений показывает, что экспериментальная оценка точности измерительных приборов и систем ведется вначале при нормальных условиях, а затем при отклонениях условий измерений от нормальных. Поэтому принято делить статические и динамические погрешности на две части: основная и дополнительная погрешности.
Основная статическая погрешность имеет место при проведении измерений в нормальных условиях, которые определяются следующими значениями климатических факторов: давление воздуха 760 мм рт. ст., температура 20±5ºC, влажность 20¸60%. При этом за рабочее положение прибора принимается то, которое указано либо на шкале или в его паспорте. Кроме того, предполагается отсутствие переносных линейных и угловых ускорений, нормальный режим питания и т. п.
Основная статическая погрешность прибора или системы возникает под влиянием многих факторов, она формируется на всех этапах проектирования и изготовления измерительного прибора или системы.
Основную погрешность, в зависимости от причин ее появления можно разделить на следующие виды:
· погрешность приближения;
· погрешность от изменения внутренних параметров измерительного прибора
или системы;
· погрешность от вредных внутренних воздействий (от действия внутренних
дестабилизирующих факторов).
Дополнительной погрешностью называется та часть статической погрешности, которая добавляется к основной погрешности при отклонении условий работы прибора или системы от нормальных.
Условия работы измерительных приборов и систем характеризуются комплексом внешних параметров, к числу которых относятся климатические (давление, температура, влажность); механические (наклоны, переносные линейные и угловые ускорения); параметры режимов питания (напряжение, частота, давление, расход); параметры внешних полей (магнитных, электрических); параметры радиационных излучений и т. п.
Отклонение внешних параметров от их номинальных значений приводит к изменению внутренних параметров и внутренних вредных воздействий или к появлению новых вредных воздействий существенно влияющих на работу приборов и систем. В итоге и появляется дополнительная погрешность прибора (системы).
Можно рассматривать частную дополнительную погрешность, т. е. погрешность, возникающую под влиянием только одного дестабилизирующего фактора, например дополнительную погрешность, обусловленную изменением окружающей температуры или режима питания и т. п.
Динамическую погрешность, так же как и статическую можно разделить на две составляющие – основную и дополнительную.
Основная динамическая погрешность имеет место при нормальных условиях работы измерительного прибора или системы.
Основную динамическую погрешность можно, в свою очередь, разделить на собственную и вынужденную.
Источниками собственной динамической погрешности являются инерционные и демпфирующие элементы прибора (системы), характеризуемые определенными параметрами (массой, моментом инерции, коэффициентом демпфирования, индуктивностью, емкостью и т. п.). Наличие в измерительной цепи прибора или системы указанных элементов приводит к запаздыванию процессов преобразования и передачи информации, а также и динамическим искажениям выходного сигнала прибора или системы.
Источниками вынужденной динамической погрешности являются внутренние шумы и наводки, под влиянием которых в измерительной цепи прибора или системы генерируется паразитная переменная составляющая сигнала.
В отличие от собственной динамической погрешности, которая проявляется только при изменении входной величины x, источники шумов и помех создают вынужденную динамическую погрешность в виде переменной составляющей в выходном сигнале, даже если входная величина x сохраняет постоянное значение и не сопровождается входной помехой.
Дополнительная динамическая погрешность возникает при отклонении условий работы измерительного прибора и системы от нормальных. В результате значение параметров внешних воздействий существенно отличается от номинальных, что и является причиной появления дополнительной погрешности. Внешние воздействия, под влиянием которых возникает дополнительная динамическая погрешность, можно разделить на следующие виды: климатические воздействия; механические воздействия (например, линейная или угловая вибрация, удары), электрические и электромагнитные воздействия (наводки, помехи, пульсации напряжения питания), помехи, сопровождающие полезный сигнал на входе измерительного прибора или системы.
2.2. Оценка случайных погрешностей измерительных
приборов и систем
В общем случае входные сигналы и возмущающие воздействия (помехи и шумы) измерительных приборов и систем являются случайными, поэтому при одних и тех же условиях погрешности приборов и систем имеют различные размеры. Размер случайных погрешностей можно оценить с использованием подходов, разработанных в теории вероятностей [ ].
Согласно положениям теории вероятностей случайная погрешность Δx наиболее полно характеризуется интегральной функцией распределения F(Δx) или дифференциальной функцией (плотностью) распределения вероятности f(Δx), связанных между собой соотношениями
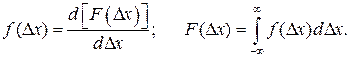 (2.10)
(2.10)
Интегральная функция распределения отражает значение вероятности появления размера погрешности не больше некоторой текущей величины Δxт
F(Δx)=P[δx< Δxт]. (2.11)
Это неубывающая функция случайной погрешности Δx (рис. 2.2, а), изменяющаяся от F(–∞)=0 до F(∞)=1.
Дифференциальная функция распределения f(Δx) (рис. 2.2, б) обычно называемая плотностью распределения вероятности, является положительной и удовлетворяет условию нормирования
Вероятность P распределения погрешности Δx в интервале, ограниченной значениями Δxн и Δxв, определяется интегрированием плотности вероятности
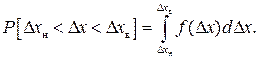 (2.13)
(2.13)
Законы распределения случайной погрешности Δx характеризуют некоторыми численными значениями – неслучайными статистическими моментами.
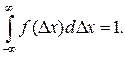 (2.12)
(2.12)
Первый начальный момент или математическое ожидание погрешности 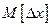 определяют для непрерывной функции распределения зависимостью
определяют для непрерывной функции распределения зависимостью
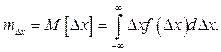 (2.14)
(2.14)
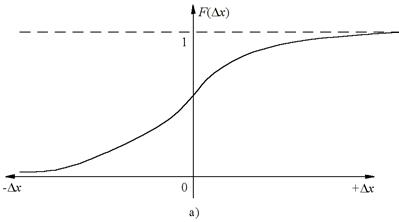
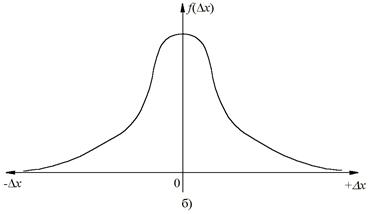
Рис. 2.2. Характер изменения интегральной функции распределения (а)
и плотности распределения вероятности случайной погрешности (б)
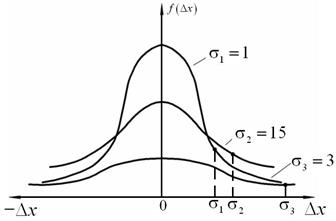
Рис. 2.3. Графики изменения плотности вероятностей случайной погрешности
Отклонение случайной погрешности от математического ожидания определяют дисперсией DΔx, т. е. вторым центральным моментом
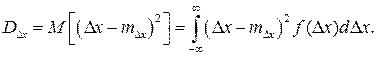 (2.15)
(2.15)
Второй начальный момент или начальный момент второго порядка для случайной погрешности определяют квадратом среднеквадратического значения случайной погрешности
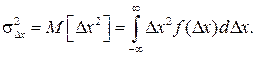 (2.16)
(2.16)
В случае mΔx=0, т. е. при отсутствии систематической составляющей погрешности, среднеквадратическое значение погрешности σΔx определяется как корень квадратный из дисперсии DΔx,
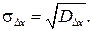 (2.17)
(2.17)
Дисперсия погрешности характеризует как бы мощность, степень рассеяния погрешности, другими словами действующее или эффективное значение случайной погрешности.
Важнейшим дополнением моментов первого и второго порядков является центральный или начальный момент второго порядка для двумерного закона распределения, учитывающего зависимость погрешности от времени Δx(t), который называют корреляционной функцией
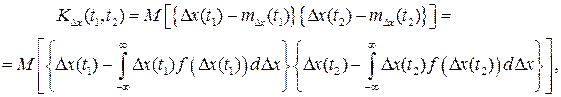 (2.18)
(2.18)
где Δx(t1) и f(Δx(t1)), Δx(t2) и f(Δx(t2)) – реализация случайной погрешности и плотности распределения погрешности в момент времени t1 и t2.
Для стационарной случайной погрешности, когда mΔx(t)= mΔx, DΔx(t)= DΔx степень связи размеров случайной погрешности Δx(t) в различные моменты времени t1 и t2 определяют автокорреляционной функцией KΔx(τ), которая зависит только от разности моментов времени τ= t2 – t1.
Для нецентрированных погрешностей с математическим ожиданием M[Δx(t)]≠0 при увеличении интервала τ корреляционная функция стремится к квадрату математического ожидания погрешности, т. е.
KΔx(τ)|τ→0 → [mΔx]2. (2.19)
В случае отсутствия статистической связи погрешности и времени t при τ→∞ KΔx(τ)|τ→¥ → 0.
При уменьшении интервала τ до нуля корреляционная функция увеличивается до значений, совпадающих с дисперсией
KΔx(τ)|τ→0 → D[Δx(t)]. (2.20)
Свойство эргодичности стационарных случайных погрешностей позволяет определить математическое ожидание, дисперсию и корреляционную функцию по ограниченному числу реализаций или по одной реализации путем осреднения погрешностей и их характеристик на достаточно большом периоде времени Т. Для этого используются следующие выражения:
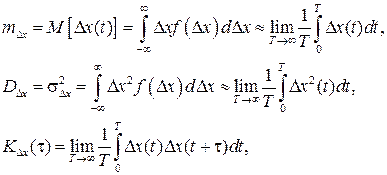 (2.21)
(2.21)
где Δx(t) – реализация случайной погрешности.
При анализе случайных погрешностей чаще всего в практике инженерных расчетов используют нормальную и равномерную плотности распределения.
Если выполнится предположение о том, что погрешности измерения могут принимать непрерывный ряд значений, то при большом числе измерений частота появления погрешностей, равных по абсолютной величине, но различного знака – одинакова и малые погрешности встречаются чаще, чем большие. Поэтому для описания случайных погрешностей следует применять нормальный (Гауссовский) закон распределения вероятностей
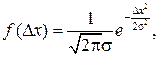 (2.22)
(2.22)
где f(Δx) – плотность вероятностей случайной погрешности Δх; σΔx – среднее квадратическое значение случайной погрешности.
На рис. 2.3 показаны кривые изменения плотности вероятностей f(Δx) при различных значениях σΔx= σi.
Из графиков на рис. 2.3 видно, что при малых значениях σi вероятнее получить малую погрешность измерений, чем большую.
Вероятность того, что погрешность измерения находится между заданными значениями Δx1 и Δx2, вычисляется по формуле
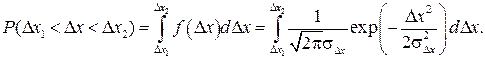 (2.23)
(2.23)
Интеграл в формуле (2.23) можно вычислить, используя таблицы функции Лапласа [ ]
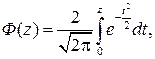 (2.24)
(2.24)
где
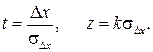
Тогда величина 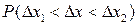 определяется соотношением
определяется соотношением
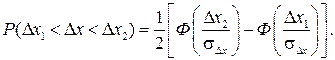 (2.25)
(2.25)
В табл. 2.1 приведены значения вероятностей для интервалов [Δx1; Δx2], заданных в единицах 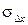 [9].
[9].
Таблица 2.1
| Интервал [Δx1;Δx2] | Вероятность P попадания погрешности в интервал [Δx1; Δx2] | 1–P |
| [- 2/3 σΔx + 2/3 σΔx] [- σΔx + σΔx] [- 2σΔx + 2σΔx] [- 3σΔx + 3σΔx] [- 4σΔx + 4σΔx] | 0,5 0,68 0,95 0,997 0,9993 | 0,5 0,32 0,05 0,003 0,00007 |
Значение погрешности, равной 2/3 σΔx называют вероятной погрешностью, а значение 3σΔx часто считают наибольшей возможной (предельной) погрешностью. Однако при большом числе измерений (n>20÷30) максимальная погрешность нередко может превышать 3σΔx.
Как уже отмечалось, часто закон распределения погрешностей можно принимать равномерным
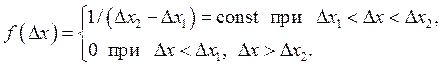 (2.26)
(2.26)
Математическое ожидание погрешности будет 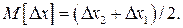 Дисперсия
Дисперсия 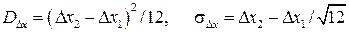 при M[Δx]=0.
при M[Δx]=0.
Для треугольного закона распределения (закона Симпсона)
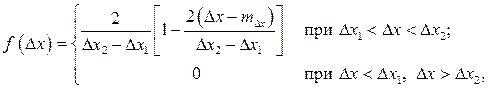 (2.27)
(2.27)
где mΔx =(Δx1 + Δx2)/2 – математическое ожидание, DΔx= (Δx2 – Δx1)2/24 – дисперсия.
В общем случае случайные погрешности Δy на выходе измерительных приборов и систем зависят от значения измеряемой величины x и характеризуются условными законами распределения, которые могут быть представлены в виде:
а) условной функции распределения F(Δy/x), выражающей условную вероятность появления случайной погрешности в интервале от - ∞ до Δy при данном значении x;
б) условной плотности распределения, являющейся производной условной функции распределения
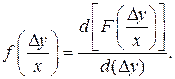 (2.28)
(2.28)
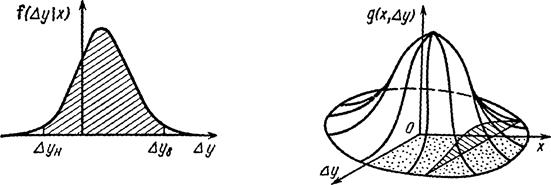
Геометрически условная плотность распределения изображается кривой, форма которой зависит от характера распределения (рис. 2.4, а). Условная вероятность попадания случайной погрешности Δy в поле допусков
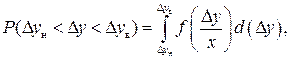 (2.29)
(2.29)
где Δyн и Δyв – нижняя и верхняя границы поля допусков на величину Δy при данном значении x. На рис. 2.4, а эта вероятность выражается заштрихованной площадью.
а) б)
Рис. 2.4. Условная плотность распределения случайной погрешности (а) и плотность распределения системы случайных величин x и Δy (б).
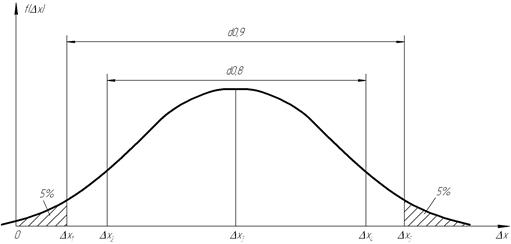
Рис. 2.5. Доверительные вероятности и доверительные интервалы случайных погрешностей
Для перехода от условного распределения к безусловному следует рассматривать систему двух случайных величин, одной из которых является измеряемая величина x, другой – погрешность Δy.
Система двух случайных величин (x, Δy) геометрически интерпретируется как случайная точка на плоскости x, Δy или как случайный вектор, составляющими которого являются случайные величины x и Δy.
Плотность распределения системы x, Δy связана с условной плотностью распределения Δy формулой
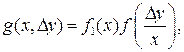 (2.30)
(2.30)
где f1(x) – безусловная плотность распределения x (распределение x не зависит от Δy).
Геометрически плотность распределения системы g(x, Δy) изображаются поверхностью (рис. 2.4, б). Величина f1(x) выражается площадью сечения функции g(x, Δy) плоскостью, проходящей через точку x перпендикулярно к оси x (см. заштрихованную площадь на рис. 2.4, б), а условная плотность f(Δy/x) равна ординате кривой, огибающей это сечение, деленной на площадь сечения.
Безусловная вероятность попадания случайной точки x, Δy в произвольное поле допусков G определяется формулой
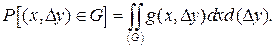 (2.31)
(2.31)
Эта вероятность геометрически выражается объемом призмы, опирающейся на сечение G в плоскости x, Δy и ограниченной сверху поверхностью g(x, Δy).
Квантильные оценки случайных погрешностей измерительных
Приборов и систем
Если построить кривую плотности распределения f(Δx) случайной погрешности Δx измерительного прибора или системы (рис. 2.5), то согласно правила нормирования площадь под кривой равна единице, т. е. отражает вероятность всех возможных событий.
Эту площадь под кривой можно разделить на некоторые части вертикальными линиями. Абсциссы таких линий называются квантилями. Так Δx= Δx1 есть 5% - ная квантиль, так как площадь слева от нее составляет 5% всей площади, а справа 95% . Соответственно значения Δx2, Δx3, Δx4 и Δx5 на рис. 2.5 будут 10% - ная, 50% - ная, 90% - ная и 95% - ная квантили. Интервал значений погрешности Δx между Δx1= Δx0,05 и Δx5= Δx0,95 охватывает 90% всех возможных значений случайной погрешности и называется интерквантильным промежутком d0,9 с 90% - ной доверительной вероятностью. Его протяженность d0,9= Δx0,95 - Δx0,05. Интерквантильный промежуток d0,8= Δx0,9 - Δx0,1 и включает в себя 80% всех возможных значений случайной погрешности Δx.
На основании такого подхода вводится понятие квантильных оценок случайной погрешности, т. е. значений погрешности с заданной доверительной вероятностью Pд как границу отрезка ± Δxд=± dд/2, на протяжении которого встречается Pд процентов всех значений случайной погрешности, а (1–Pд) процентов общего числа возможных значений погрешности оказывается за границами этого интервала.
Таким образом, чтобы характеризовать случайную погрешность достаточно полно, надо располагать двумя числами доверительной вероятности Pд и соответствующим доверительным интервалом ± Δxд. Полученная оценка случайной погрешности есть указание "максимального" значения погрешности Δxд с заданной доверительной вероятностью Pд. Для нормирования случайной и результирующей погрешности средств измерений используются значения доверительных вероятностей Pд=0,9 и Pд=0,95.
Достоинство доверительной погрешности состоит в том, что ее значение может быть оценено по экспериментальным данным.
При проведении некоторого ряда измерений можно определить среднее арифметическое значение измеряемой величины 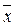 , которая является оценкой истинного значения измеряемой величины xи. Значение измеряемой величины
, которая является оценкой истинного значения измеряемой величины xи. Значение измеряемой величины 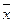 как правило не совпадает с истинным ее значением, а отклоняется от него на величину погрешности Δx =
как правило не совпадает с истинным ее значением, а отклоняется от него на величину погрешности Δx = 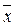 – xи.
– xи.
Доверительная вероятность Pд есть вероятность того, что 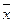 отличается от xи не более чем на Δxд.
отличается от xи не более чем на Δxд.
При небольшом числе измерений (n<20), результаты измерений подчиняются нормальному закону распределения и поэтому для определения погрешности с заданной доверительной вероятностью Pд целесообразно использовать распределение Стьюдента.
В табл. 2.2. приведены так называемые квантили распределения Стьюдента | 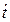 (n)|Pд при заданной доверительной вероятности Pд=0,8÷0,99 для числа измерений n=2-30 [9].
(n)|Pд при заданной доверительной вероятности Pд=0,8÷0,99 для числа измерений n=2-30 [9].
Квантили распределения Стьюдента Таблица 2.2.
| Число измерений n | Доверительная вероятность Pд | ||||
| 0,8 | 0,9 | 0,95 | 0,98 | 0,99 | |
| 3,08 1,89 1,64 1,53 1,38 1,33 1,31 | 6,31 2,92 2,35 2,13 1,84 1,73 1,70 | 12,7 4,30 3,18 2,77 2,26 2,09 2,04 | 31,8 6,96 4,54 3,75 2,82 2,54 2,47 | 63,7 9,92 5,84 4,60 3,25 2,87 2,76 |
Чтобы найти доверительный интервал ± Δxд, необходимо для данных n и Pд найти квантиль | 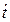 (n)|Pд и вычислить
(n)|Pд и вычислить
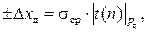 (2.32)
(2.32)
где σср – среднее значение средней квадратической погрешности σΔx ряда измерений.
Среднее квадратическое значение погрешности n измерений определяется
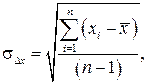 (2.33)
(2.33)
где xi – результат i-го измерения.
Тогда среднее значение σср определяется как
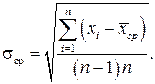 (2.34)
(2.34)
При этом следует иметь в виду, что по ограниченным экспериментальным данным не могут быть получены точные доверительные значения случайной погрешности, а только лишь приближенные значения – оценки. Поэтому квантильные оценки с большими доверительными вероятностями могут быть найдены только при большом числе измерений.
Число измерений n, необходимо для определения Δxд с заданной вероятностью Pд определяется соотношением
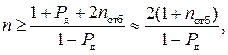 (2.35)
(2.35)
где nотб – число результатов измерений из общего числа n, которые имеют наибольшие по модулю отклонения xi от среднеарифметического значения 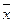 .
.
Для различных значений Pд и nотб необходимое число измерений n приведено в табл. 2.3 [10].
Таблица 2.3
| Pд | Необходимое n при | ||
| nотб=0 | nотб=1 | nотб=2 | |
| 0,8 0,9 0,95 0,99 0,995 0,997 |
Основным недостатком оценки случайной погрешности доверительным значением Δхд при произвольно выбираемом Pд является невозможность суммирования доверительных значений случайной погрешности с разными доверительными вероятностями.
Дата добавления: 2020-10-25; просмотров: 341;










