ФУНКЦИЯ, ПРЕОБРАЗОВАНИЕ

ФУНКЦИЯ

Рассмотрим типичный случай бинарного отношения (А, В, F), когда каждому элементу множества А соответствует не более одного элемента из множества В. Такое отношение называется функциональным или, что тоже самое, функцией.

Пусть А - множество пальто учеников вашей школы, В - множество крючков в гардеробе вашей школы. График бинарного отношения строится так: рассматриваются те и только те пары, где на первом месте стоит пальто ученика, а на втором - крючок, на котором это пальто висит. Если часть пальто повешена, причем неважно, по одному или по несколько на крючок, но ни одно пальто не повешено на два или более крючков, то мы получим соответствие, при котором каждому элементу множества А соответствует не более одного элемента из множества В. Тому пальто, которое висит, соответствует крючок, а тому, которое не висит, не соответствует ни одного крючка.

Понятие функции уходит своими корнями в ту далекую эпоху, когда люди впервые поняли, что окружающие их явления взаимосвязаны. Термин “функция” стали применять в конце ХVII века Лейбниц (1646-1716) и его ученики.

Определение. Бинарное отношение (Х, Y, f) между множествами X и Y называется функциональным (или функцией из множества X в множество Y, или частичным отображением множества X в Y), если каждому элементу множества X соответствует не более одного элемента множества Y, то есть каждый элемент множества X или находится в отношении f точно с одним элементом множества Y, или не находится в отношении f ни с одним элементом множества Y.

Обратим внимание на то, что для сокращения речи иногда говорят просто о функции f, но всегда при этом следует отчетливо представлять, между элементами каких множеств X и Y она рассматривается, так как просто функция без множеств X и Y не существует. Функция f из множества X в множество Y - это особо важный случай бинарного отношения между множествами X и Y. Рассмотрим соответствие f: “y½x” между множествами X={1, 4, 8} и Y={2}.

Соответствие f={(4, 2); (8, 2)} является функцией из Х в Y.

Определение. Пусть (X, Y, f) есть бинарное отношение между множествами Х и Y, то есть fÌ(Х´Y). Множество первых элементов пар называется областью определения отношения f, множество вторых элементов пар - областью значений отношения f. Область определения f обозначается D(f), область значений f обозначается E(f).

Так, областью определения отношения в предыдущем примере является множество {4,8}, а областью значений - множество {2}.

Пример. Рассмотрим соответствие f: “y½x” между множествами Х={2, 10, 15}; Y={1, 2, 5}; D(f)={2, 10, 15}; E(f)={1, 2, 5}.

Это соответствие не является функциональным, так как элементу 2 соответствуют два различных элемента 1 и 2 (1½2 и 2½2).

Рассмотрим важный частный случай функционального соответствия между множествами X и Y, при котором X=D(f).

Определение. Если (X, Y, f) - функция из множества X во множество Y и X=D(f), то f называется отображением (полным отображением) множества X в Y.

В этом случае f есть функция из X в Y с областью определения X и говорят, что f всюду определена на X. Если f - отображение из Х в Y, то каждому элементу из множества X соответствует точно один элемент из множества Y.

Пусть А - множество всех прямоугольников на плоскости, Â⁺={xνx>0}, f(a)=S(а), где аÎA, S(a) - площадь прямоугольника а. Мы получим бинарное отношение между множествами А и Â⁺. Является ли это отношение отображением А в Â⁺? Да, является, так как если прямоугольники равны, то равны и их площади. D(f)=А ; Е(f)= Â⁺.

Определение. Пусть f - отображение множества Х в множество Y. Если E(f)=Y, то f называется отображением множества X на множество Y, или сюръекцией (от французского слова súr - “на”). Заметим, что отображение “на” является частным случаем отображения “в”.

В примере с пальто и крючками отображение будет сюръективным, если все крючки заняты, то есть положение таково, что все пальто развешены и все крючки использованы. Рассмотрим еще пример:

А={1, 2, 3, 4}, В={1, 2, 3, 4, 5}, f={(1, 2); (2, 3); (3, 4); (4, 5)}.

Является ли f отображением А в B? Да, является, D(f)=А, E(f)={2, 3, 4, 5}, следовательно, f не сюръективное отображение. Кроме того, f обладает еще одним свойством: если а₁ , а₂Î А, а₁¹ а₂, то и f(а₁)¹f(а₂).

Определение. Отображение f множества X в множество Y называется взаимно однозначным, или инъективным, если из того, что (а₁,b)Îf и (а₂,b)Îf, следует, что a₁=a₂. Очевидно, что инъективность имеет место тогда и только тогда, когда из а₁¹ а₂ следует f(а₁)¹f(а₂).

В примере с пальто мы получим взаимно однозначное отображение, если на каждом крючке или не висит ни одного пальто, или висит только одно пальто.

Определение. Отображение f множества X в множество Y называется биективным (от латинского слова “bis” - два), или биекцией, или взаимно-однозначным соответствием, если оно инъективно и сюръективно.

Рассмотрим пример: А=Â, B=Â⁺={хνx>0}, f(x)=2^x . Тогда f - биекция  на Â⁺.

Виды отображений:

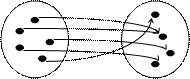
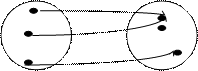
Х Y X Y

Отображение X в Y, но не Х на Y Отображение X на Y но не инъекция

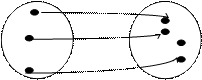
Х Y X Y

Инъекция, но не сюръекция Биекция

ПРЕОБРАЗОВАНИЕ

Перейдем к изучению понятия преобразования.

Определение. Отображение f множества А в себя называется преобразованием множества А.

Преобразование, как следует из определения, является частным случаем бинарного отношения на А. Рассмотрим примеры преобразований.

1. Пусть a - плоскость, а f - множество пар точек плоскости, таких, что первая компонента есть некоторая точка b, а вторая - образ этой точки при повороте на 90°. Тогда (a, a, f) есть преобразование плоскости a. Такое преобразование плоскости a называется поворотом плоскости a на угол 90°.

2. Пусть Â - множество всех вещественных чисел, f={(x,sinx)½xÎÂ}, тогда (Â, Â, f) - преобразование плоскости.

Определение. Пусть f и g - преобразования множества А. Композицией преобразований f и g называется преобразование fg множества А такое, что (fg)(u)=f(g(u)).

Для того чтобы осуществить композицию преобразований, нужно сначала осуществить второе преобразование, а потом первое. В геометрии обычно рассматриваются только те преобразования, которые являются биективными отображениями, то есть только биективные преобразования. Повороты плоскости, конечно, являются биективными преобразованиями, а рассмотренное ранее преобразование (Â,Â,f), где f=={(x, sinx)½xÎÂ}, не является биективным преобразованием.