Теорема о делении с остатком

В этом параграфе будем рассматривать только многочлены, заданные над полем. В кольце многочленов справедлива теорема о делении с остатком.

Теорема 3. "f(x),g(x)ÎР[x]$!q(x),r(x)ÎР[x] (f(x)=g(x)q(x)+r(x)), причем r(x)=0 или степень r(x)< степени g(x).

Доказательство

I. Докажем возможность представления. Пусть deg f(x)=n, deg g(x)=s.

1. Если n < s, тогда f(x) = g(x)0 + f(x), то есть q(x) = 0, а r(x) = f(x) и

deg r(x)<deg g(x), следовательно, теорема верна.

2. Пусть n ³ s, f(x)=a_nxⁿ+a_n-1x^n-1+…+a₁x+a₀, g(x)=b_sx^s+b_s-1x^s-1+…+b₁x+b₀

Рассмотрим многочлен вида

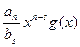и найдем разность

f(x)- 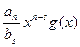= f₁(x), (*)

где f₁(x)=с_n₁xⁿ¹+…+c₁x+c₀. Очевидно, n1<n.

Аналогично, продолжаем вычислять разности до тех пор, пока не получим в результате 0 или многочлен, степени меньшей s, имеем

f₁(x)- 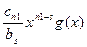= f₂(x)= d_n2xⁿ²+…+d₁x+d₀ (*)

f₂ (x)- 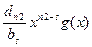= f₃(x) (*)

……………………………

f_k_-1(x)- 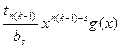= f_k(x), (*)

где deg f_k(x) < deg g(x) или f_k(x)=0.

Очевидно, что на каждом следующем шаге алгоритма получается многочлен степени строго меньшей, чем предыдущий, то есть получим цепочку неравенств deg f(x)> deg f₁(x)> deg f₂(x)> deg f₃(x)>…> deg f_k_-1(x)> deg f_k(x). Так как степени всех многочленов – это положительные целые числа, заключенные в промежутке от s до n, а таких чисел существует только конечное число, то алгоритм конечен. Сложив равенства (*), получим

f(x)- 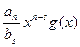+f₁(x)- 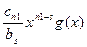+f₂(x)- 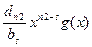+…+f_k-1(x)- =

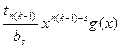= f₁(x)+ f₂(x)+ f₃(x)+…+ f_k(x)

Это равносильно

f(x)–( 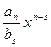+ + 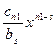+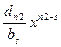…+ 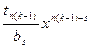)g(x)=f_k(x) и deg f_k(x)<deg g(x) или f_k(x)=0.

Обозначив f_k(x)=r(x), а 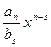+ + 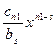+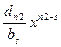…+ 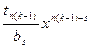=q(x), получим f(x)-q(x)g(x)=r(x), что равносильно f(x)=q(x)g(x)+r(x) и deg r(x)<deg g(x) или r(x)=0. Возможность представления доказана.

II. Докажем единственность. Предположим противное, пусть найдутся по крайней мере, два различных представления f(x)=q(x)g(x)+r(x), где deg r(x)<deg g(x) или r(x)=0 и f(x)=q₁(x)g(x)+r₁(x), где deg r₁(x)<deg g(x) или r₁(x)=0

Получим q(x)g(x)+r(x)=q₁(x)g(x)+r₁(x)Ûq(x)g(x)-q₁(x)g(x)=r₁(x)-r(x)Û

Û (q(x)-q₁(x))g(x)=r₁(x)-r(x).

Так как deg (q(x)-q₁(x))g(x)³ deg g(x), а deg (r₁(x)-r(x))<deg g(x), то последнее равенство приводит нас к противоречию. Следовательно, наше предположение неверно, и единственность доказана.

Если f(x)=q(x)g(x)+r(x), то многочлен q(x) называется неполным частным или просто частным от деления многочлена f(x) на многочлен g(x), а многочлен r(x) - остатком от деления.

следствие 1. Многочлен f(x) делится на многочлен g(x) тогда и только тогда, когда остаток от деления r(x)=0.

следствие 2. Алгоритм, приведенный при доказательстве теоремы, лежит в основе метода деления многочлена на многочлен «уголком».

Пример. Найти остаток от деления многочлена f(x)=3х⁵-7х⁴+х³+3х²-х+8 на многочлен g(x)=х³+2х²-х-1.