Дублирование информации

Данный метод является простейшим видом контроля, заключающимся в повторной передаче данных. Достоинство метода дублирования информации: простая реализация. Недостаток: снижение пропускной способности в два раза из-за высокой избыточности.

Кодирование данных и передача по линии связи :

1. Выбор данного .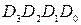

2. Получение копии данного .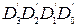

3. Передача данного и его копии 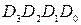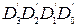по линии связи.

Прием и проверка данных:

1. Прием данного .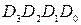

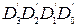2. Вычисление поверочных битов 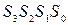сравнением данного 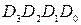и его копии 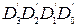с помощью логической операции «сумма по модулю два». Операция сумма по модулю два (исключающее ИЛИ, неравнозначность, XOR) выполняется по правилам: 0 Å 0 = 0; 0 Å 1 = 1; 1 Å 0 = 1; 1 Å 1 = 0.

Для многоразрядных двоичных чисел операция сумма по модулю два выполняется поразрядно: .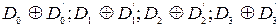

Вычисление поверочных битов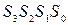

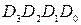
		Данное
		Операция сумма по модулю два
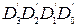
		Копия данного
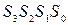
		Поверочные биты

3. Проверка на наличие ошибок:

- если поверочные биты 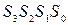равны нулю, то ошибки нет;

- если поверочные биты 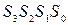содержат хотя бы одну единицу, то ошибка есть.

Пример. Передача данного 1101.

Кодирование данных и передача по линии связи :

1. Передача данного и его копии 1101 1101.

Прием и проверка данных:

1. Прием данных 1101 1101.

2. Вычисление поверочных битов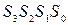

		Данное.
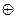
		Операция сумма по модулю два.
		Копия данного.
		Поверочные биты .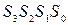

3. Проверка на наличие ошибок:

- поверочные биты 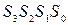равны нулю - ошибки нет.

Пример.

Кодирование данных и передача по линии связи :

1. Передача данного и его копии 1101 1101.

Прием и проверка данных:

1. Прием данных 1101 0101.

2. Вычисление поверочных битов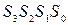

		Данное.
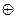
		Операция сумма по модулю два.
		Копия данного.
		Поверочные биты .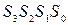

3. Проверка на наличие ошибок:

- поверочные биты 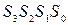равны не нулю - ошибка есть.

В других методах (контрольная сумма, контроль паритета, код Хемминга, CRC, код Рида-Соломона, коды БЧХ) применяют помехоустойчивые коды, которые рассчитываются по специальным алгоритмам. Код Хемминга, CRC, Рида-Соломона, БЧХ относятся к линейным блоковым кодам.

Различные коды позволяют выявлять одиночные и множественные ошибки, а также исправлять одиночные и множественные ошибки.

Контрольная сумма

Контрольные суммы используются для обнаружения ошибок в протоколах UDP (User Datаgramm Protocol) транспортного уровня компьютерных сетей (Интернет).

Помехоустойчивое кодирование методом контрольной суммы позволяет:

1. Обнаруживать одиночные ошибки.

2. Обнаруживать множественные ошибки.

Порядок работы метода.

Кодирование данных и передача по линии связи :

1. Вычисление арифметической суммы данных (без учета переноса).

2. Вычисление контрольной суммы поразрядной инверсией суммы.

3. Передача данного и контрольной суммы.

Прием и проверка данных:

1. Прием данного и контрольной суммы.

2. Вычисление суммы принятых данных.

3. Вычисление поверочных битов, сложением суммы и контрольной суммы.

4. Проверка на наличие ошибок:

- если поверочные биты не содержат нулей, то ошибки нет.

- если поверочные биты содержат хотя бы один нуль, то есть ошибка.

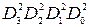Пример. Требуется передать два данных = 1100 и = 0110.

Кодирование данных и передача по линии связи :

1. Вычисление суммы данных = + :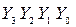

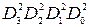		Первое данное .
+		Арифметическое сложение.
		Второе данное .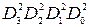
		Сумма .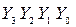

2. Вычисление контрольной суммы = :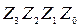

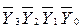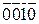
	Поразрядная инверсия суммы .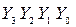
	Контрольная сумма .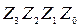

3. Передача данных и контрольной суммы:

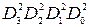
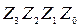= 1100 0110 1101.

Прием и проверка данных:

1. Прием данных и контрольной суммы:

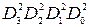
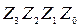= 1100 0110 1101.

2. Вычисление суммы данных: = + :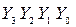

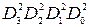		Первое данное .
+		Арифметическое сложение.
		Второе данное .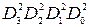
		Сумма .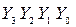

3. Вычисление поверочных битов = + :

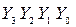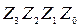	Сумма .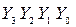
+	Арифметическое сложение.
	Контрольная сумма .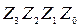
	Поверочные биты .

4. Проверка на наличие ошибок:

- поверочные биты не содержат нулей - ошибки нет.

Пример.

Кодирование данных и передача по линии связи :

1. Передача данных и контрольной суммы:

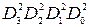
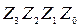= 1100 0110 1101.

Прием и проверка данных:

1. Прием данных и контрольной суммы:

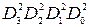
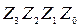= 1100 1110 1101.

2. Вычисление суммы данных: = + :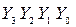

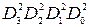		Первое данное .
+		Арифметическое сложение.
		Второе данное .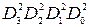
		Сумма .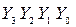

3. Вычисление поверочных битов = + :

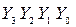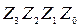	Сумма .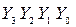
+	Арифметическое сложение.
	Контрольная сумма .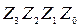
	Поверочные биты .

4. Проверка на наличие ошибок:

- поверочные биты содержат нули - ошибка есть.

Контроль паритета

Помехоустойчивое кодирование методом контроля паритета позволяет:

1. Обнаруживать одиночные ошибки.

2. Обнаруживать ошибки нечетной кратности (ошибки одновременно в одном, трех, пяти и т.д. битах).

Контроль паритета не позволяет обнаруживать ошибки четной кратности (ошибки одновременно в двух, четырех, шести и т.д. битах).

При контроле паритета передающий узел вычисляет один контрольный бит паритета Р для данных D_n-1D_n-2…D₁D₀ (обычно n = 5, 6, 7, 8 бит). Различают два типа контроля паритета (parity – соответствие, аналогия): по четности и по нечетности.

При контроле по четности сумма единичных битов данного и бита паритета является четным числом. При контроле по нечетности сумма единичных битов данного и бита паритета является нечетным числом.

Кодирование данных и передача по линии связи :

1. Вычисление бита паритета Р для данного D_n-1D_n-2…D₁D₀:

Р = (D_n-1 Å D_n-2 Å… Å D₁ Å D₀) Å V,

где V определяет вид используемого паритета (V = 0 – контроль по четности; V = 1 – контроль по нечетности).

2. Формирование сообщения, содержащего данное D_n-1D_n-2…D₁D₀ и бит паритета Р.

3. Передача сообщения D_n-1D_n-2…D₁D₀ Р по линии связи.

Прием и проверка данных:

1. Прием сообщения D_n-1D_n-2…D₁D₀ Р.

2. Вычисление поверочного бита S = (D_n-1 Å D_n-2 Å … Å D₁ Å D₀) Å V;

3. Проверка на наличие ошибок:

- если поверочный бит S = 0, ошибки нет (ошибка не обнаружена);

- если поверочный бит S = 1, ошибка есть.

Бит контроля по четности Рч вычисляется по формуле:

Рч = (D_n-1 Å D_n-2 Å … Å D₁ Å D₀) Å 0

Пример контроля по четности (V = 0).

Кодирование данных и передача по линии связи :

1. Вычисление бита паритета Рч для данного 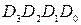= 1101.

Рч = (1 Å 1 Å 0 Å 1) Å 0 = (0 Å 0 Å 1) Å 0 = (0 Å 1) Å 0 = 1 Å 0 = 1.

2. Формирование сообщения, содержащего данное 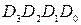= 1101 и бит паритета Рч =1.

3. Передача сообщения 1101 1 по линии связи.

Прием и проверка данных (вариант 1 без ошибки):

1. Прием сообщения 1101 1.

2. Вычисление поверочного бита S = (1 Å 1 Å 0 Å 1 Å 1) Å 0

= (0 Å 0 Å 1 Å 1) Å 0 = (0 Å 1 Å 1) Å 0 = (1 Å 1) Å 0 = 0 Å 0 = 0.

3. Проверка на наличие ошибок:

- поверочный бит S = 0 - ошибки нет.

Прием и проверка данных (вариант 2 с одной ошибкой):

1. Прием сообщения 1101 1..

2. Вычисление поверочного бита S = (1 Å 0 Å 0 Å 1 Å 1) Å 0

= (1 Å 0 Å 1 Å 1) Å 0 = (1 Å 1 Å 1) Å 0 = (0 Å 1) Å 0 = 1 Å 0 = 1.

3. Проверка на наличие ошибок:

- поверочный бит S = 1 – ошибка есть (одна ошибка обнаружена).

Прием и проверка данных (вариант 3 с двумя ошибками):

1. Прием сообщения 1101 1.

2. Вычисление поверочного бита S = (1 Å 0 Å 1 Å 1 Å 1) Å 0

= (1 Å 1 Å 1 Å 1) Å 0 = (0 Å 1 Å 1) Å 0 = (1 Å 1) Å 0 = 1 Å 0 = 0.

3. Проверка на наличие ошибок:

- поверочный бит S = 0 – ошибка не обнаружена (ошибки четной кратности не обнаруживаются).

Прием и проверка данных (вариант 3 с тремя ошибками):

1. Прием сообщения 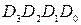= 1101 1.

2. Вычисление поверочного бита S = (1 Å 0 Å 1 Å 0 Å 1) Å 0

= (1 Å 1 Å 0 Å 1) Å 0 = (0 Å 0 Å 1) Å 0 = (0 Å 1) Å 0 = 1 Å 0 = 1.

3. Проверка на наличие ошибок:

- поверочный бит S = 1 – ошибка обнаружена (ошибки нечетной кратности обнаруживаются).

Бит контроля по нечетности Рн вычисляется по формуле:

Рн = (D_n-1 Å D_n-2 Å … Å D₁ Å D₀) Å 1.

Пример контроля по нечетности (V = 0).

Кодирование данных и передача по линии связи :

1. Вычисление бита паритета Рн для данного 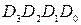= 1101.

Рн = (1 Å 1 Å 0 Å 1) Å 1 = (0 Å 0 Å 1) Å 1 = (0 Å1) Å1 = 1 Å 1 = 0.

2. Передача данного 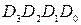= 1101 и бита паритета Рн =0 по линии связи.

Прием и проверка данных (вариант 1 без ошибки):

1. Прием данного 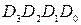= 1101 и бита паритета Рн =0.

2. Вычисление поверочного бита S = (1 Å 1Å 0 Å 1Å 0) Å 1

= (0 Å 0 Å 1 Å 0) Å 1 = (0 Å 1 Å 0) Å 1 = (1 Å 0) Å 1 = 1 Å 1 = 0.

3. Проверка на наличие ошибок:

- поверочный бит S = 0 - ошибки нет.

Прием и проверка данных (вариант 2 с одной ошибкой):

1. данного 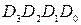= 1101 и бита паритета Рн =0.

2. Вычисление поверочного бита S = (1 Å 0 Å 0 Å 1 Å 0) Å 1

= (1 Å 0 Å 1 Å 0) Å 1 = (1 Å 1 Å 0) Å 1 = (0 Å 0) Å 1 = 0 Å 1 = 1.

3. Проверка на наличие ошибок:

- поверочный бит S = 1 – ошибка есть (одна ошибка обнаружена).

Прием и проверка данных (вариант 3 с двумя ошибками):

1. данного 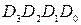= 1101 и бита паритета Рн =0.

2. Вычисление поверочного бита S = (1 Å 0 Å 1 Å 1 Å 0) Å 1

= (1 Å 1 Å 1 Å 0) Å 1 = (0 Å 1 Å 0) Å 1 = (1 Å 0) Å 1 = 1 Å 1 = 0.

3. Проверка на наличие ошибок:

- поверочный бит S = 0 – ошибка не обнаружена (ошибки четной кратности не обнаруживаются).

Прием и проверка данных (вариант 3 с тремя ошибками):

1. Прием данного 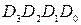= 1101 и бита паритета Рн =0.

2. Вычисление поверочного бита S = (1 Å 0 Å 1 Å 0 Å 0) Å 1

= (1 Å 1 Å 0 Å 0) Å 1 = (0 Å 0 Å 0) Å 1 = (0 Å 0) Å 1 = 0 Å 1 = 1.

3. Проверка на наличие ошибок:

- поверочный бит S = 1 – ошибка обнаружена (ошибки нечетной кратности обнаруживаются).

На практике наиболее часто применяется нечетный паритет, позволяющие фиксировать полное пропадание информации при передаче данного из нулей 00000000, так как формируется комбинация 000000001.