КРИТЕРИИ ОЦЕНКИ ПОГРЕШНОСТЕЙ

Погрешность (информационно–измерительной системы, результата измерений, результата эксперимента) – случайный процесс. Ее полной характеристикой является закон распределения, который может быть представлен в виде условной плотности распределения вероятностей или безусловной плотности распределения вероятностей , если статистическая связь между погрешностью и вектором измеряемых величин Р отсутствует. Практически использование плотности распределения вероятностей в качестве критерия погрешности сопряжено с рядом трудностей и не всегда возможно. Поэтому принято оценивать погрешности числовыми характеристиками, связанными тем или иным оператором с законом распределения. К таким характеристикам относятся экстремальные и интегральные оценки, а также оценки, основанные на применении доверительных интервалов. Плотность распределения вероятностей используется, главным образом, для оценки погрешностей экспериментальных и опытных образцов информационно–измерительных систем высокоточных внешнетраекторных измерений с целью идентификации источников погрешностей и их устранения, а также дифференциации погрешностей на случайные и систематические и изучения законов их поведения. Наиболее употребительной экстремальной оценкой погрешности является модуль максимального отклонения или, полагая здесь и ниже оператор идеальной информационно–измерительной системы тождественно равным единице и опуская индекс р в векторе выходного сигнала, имеем: В качестве наиболее употребительной интегральной оценки погрешности используется среднеквадратичное отклонение, определяемое выражением

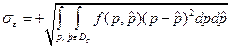
или дисперсия оценки ,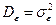

здесь D_p – область существования измеряемой величины и оценки.

Упрощенная оценка среднеквадратичного отклонения в предположении может быть получена по выражению

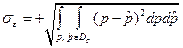
или для случая дискретных измерений

.

Значение n = 1 вместо n в знаменателе обеспечивает несмещенность оценки, 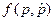– совместная плотность распределения измеряемой величины р и ее оценки . Иногда вместо среднеквадратичной погрешности используется ее интегральная оценка в виде среднего модуля отклонения

.

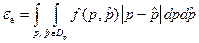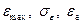представляют собой так называемые точечные оценки погрешности. Они в той или иной степени удобны в качестве оценок точности информационно–измерительной системы, отдельных технических средств и преобразований информации в процессе измерений и отработки результатов.

Интервальные или вероятностные оценки погрешностей дают более полную характеристику, чем точечные, позволяя определить вероятность , с которой погрешность не выходит за заданные пределы, 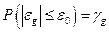. Естественно, что для определения интервальной оценки необходимо знание закона распределения вероятностей погрешности , поскольку

.

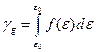С интервальной оценкой связана так называемая предельная погрешность 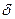, за которую условились принимать такое значение погрешности, вероятность превышения которого не более 0,003, т.е.

.

В случае нормального закона распределения погрешностей предельная погрешность связана со среднеквадратичной соотношением .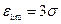

Для сравнения информационно–измерительных систем и их средств между собой, а также при совместной обработке результатов измерений, выполненных информационно–измерительными системами, обладающими различной точностью, используются оценки погрешностей в виде функций потерь, которые строятся так, чтобы малым погрешностям соответствовали меньшие потери. При этом функция потерь может быть линейной, т.е. связанной с экстремальной погрешностью соотношением 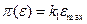, квадратичной, т.е. связанной со среднеквадратичным отклонением выражением 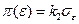, или более сложной. Из последнего выражения видно, что оценка погрешности в виде функции потерь совпадает со среднеквадратичным отклонением при .

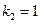Наконец, при оптимизации информационно–измерительных систем в качестве оценки погрешности используется условный 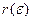или безусловный средний риск, представляющий собой усредненную функцию потерь при фиксированном значении измеряемой величины или по всем возможным значениям измеряемой величины, и определяемый выражениями

,

.

Перечисленные критерии оценки погрешностей обладают определенными преимуществами и недостатками. Чем более полон критерий, тем больше априорных сведений необходимо иметь для получения погрешности. Так, например, для использования среднего риска в качестве критерия оценки погрешности необходимо выбрать функцию потерь и знать условный закон распределения 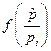оценки измеряемой величины при ее фиксированном значении или совместное распределение вероятностей измеряемой величины и ее оценки. Эти вероятностные характеристики могут быть определены только на основании натурного эксперимента. Для выбора вида функции потерь также необходимо иметь дополнительные сведения. Интервальные оценки погрешностей нашли большое применение при летных испытаниях и, особенно, для оценки точности внешнетраекторных измерений, позволяя судить, какова вероятность получения погрешности заданной величины в конкретном эксперименте. Однако, для их определения необходимо достоверное знание закона распределения погрешностей. Поэтому они используются при проведении особо ответственных летных испытаний, при паспортизации измерительной трассы, а также для исследования и оценки точности высокоточных опытных оптических и радиотехнических средств внешнетраекторных измерений. Наиболее употребительными являются оценки погрешностей в виде экстремальной и среднеквадратичного отклонения, что связано, прежде всего, с простотой их экспериментального определения. При этом экстремальные оценки целесообразны при летных испытаниях на предельных режимах, прочностных испытаниях и вообще во всех случаях, когда исследуемые процессы (объект) могут приближаться к аварийным ситуациям. Наоборот, среднеквадратичное отклонение, оценивая погрешность в среднем, удобно для общей оценки точности информационно–измерительной системы и результатов измерений, эксперимента и, главным образом, при сравнении различных информационно–измерительных систем, а также экспериментов, осуществляемых разными методами, средствами и проводимых в различных условиях.

ПОГРЕШНОСТИ ИНФОРМАЦИОННО–ИЗМЕРИТЕЛЬНЫХ СИСТЕМ.
МЕТОДЫ ОЦЕНКИ

Экспериментатор, планируя измерения, должен иметь сведения о точности подсистем информационно–измерительной системы летных испытаний (бортовой, внешнетраекторной, радиотелеметрической) для оценки ожидаемой точности измерений и сопоставления ее с требуемой. Эти сведения должны быть представлены в одних и тех же критериях. Кроме того, если бортовые датчики, согласующие устройства и регистрирующие устройства в соответствии с целью и задачами летного эксперимента выбираются или заказываются экспериментатором из большого набора приборов, выпускаемых серийно, то измерительная трасса, оснащенная средствами внешнетраекторных и радиотехнических измерений, достаточно универсальна для проведения различных летных испытаний и может быть использована в конкретном эксперименте в соответствии с ее возможностями. Таким образом, для оценки результатов летного эксперимента необходимо, прежде всего, на основе известных погрешностей отдельных средств и подсистем информационно–измерительной системы оценить ее точность в целом.

Методы оценки погрешностей одномерных измерительных устройств хорошо разработаны и в основном закреплены законодательно. Эти же методы распространяются (с определенными допущениями) на информационно–измерительные системы последовательной структуры. К ним можно отнести, например, оценку точности системы измерения какой-либо физической величины, состоящей из датчика, согласующего устройства и регистратора, или оценку точности информационно–измерительной системы, если известна погрешность измерительной системы и системы обработки.

Информационно–измерительные системы летных испытаний – системы многомерные, структура простейших из них параллельная или параллельно–последовательная. Разработка методов оценки погрешностей таких систем еще не завершена. Некоторые рекомендации для оценки их точности, изложенные в классических работах, а также используемые практически при летных испытаниях, приведены ниже.

При летных испытаниях различные физические величины имеют разные пределы измерения и требования к точности их измерения различны. В большинстве случаев целесообразна оценка погрешности информационно–измерительной системы для каждой измеряемой величины и введение критерия оценки ее погрешности в целом в виде совокупности оценок погрешности измеряемых ею физических величин

.

Например, радиотехническая измерительная система оценивается совокупностью погрешностей измерения дальности, углов визирования, скорости изменения дальности и производных углов. Точно также, погрешности n-мерной бортовой и радиотелеметрической систем оцениваются n-мерным вектором, где каждый компонент вектора – погрешность измерения одного входного сигнала.

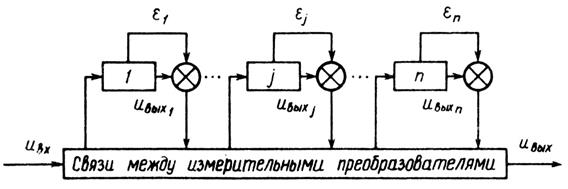
Оценка погрешности информационно–измерительной системы. Для предварительной оценки составляющих вектора основной статической погрешности N-мерной информационно–измерительной системы, состоящей из n различных преобразователей, участвующих в измерении одной физической величины, погрешности которых известны (рис. 3), имеем в линейном приближении

.

Здесь – абсолютная погрешность j-ro преобразователя; 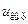– выходной сигнал, соответствующий i-й измеряемой величине; 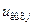– выходной сигнал j-го преобразователя; – коэффициент влияния j-го преобразователя на соответствующую компоненту погрешности информационно–измерительной системы, зависящий от типа связей.

Рис. 3. К оценке погрешностей информационно–измерительной системы:

n – количество преобразований; 1, ..., j, ..., n – преобразователи; – абсолютная погрешность j-го преобразователя; 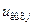– выходной сигнал j-го преобразователя;
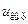– выходной сигнал информационно–измерительной системы.

При оценке относительной погрешности информационно–измерительной системы это выражение принимает вид

,

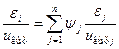где – безразмерный коэффициент влияния j-ro преобразователя.

Индекс «0» у производной в приведенном выражении подчеркивает, что коэффициент влияния вычисляется для нормальных условий. Коэффициент влияния зависит от схемы включения преобразователя в информационно–измерительной системе и от оператора преобразователя.

Если зависимости пропорциональные и связь между измерительными преобразователями последовательная, то , т.е. относительная погрешность любого преобразователя приводится к выходу информационно–измерительной системы без трансформации. Именно поэтому суммарная относительная среднеквадратичная погрешность бортовой информационно–измерительной системы оценивается выражением

,

где –~ соответствующие погрешности датчика, согласующего устройства и регистратора.

Подобный вид имеет выражение для оценки суммарной относительной среднеквадратичной погрешности информационно–измерительной системы, состоящей из измерительной системы и системы обработки 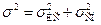, где 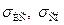– среднеквадратичные погрешности измерительной системы и системы обработки.

Каждая из составляющих погрешностей в суммарной погрешности информационно–измерительной системы оценивается теоретически и проверяется экспериментально в лабораторных условиях в соответствии с нормативными документами (ГОСТ, ОСТ, методики, инструкции). Окончательная оценка погрешности информационно–измерительной системы выполняется экспериментально в условиях, имитирующих летный эксперимент или при проведении специального летного эксперимента.