Тема № 2. Анализ работы и основы расчета механизмов двигателя. Кинематика, динамика и уравновешивание двигателей.

Основы кинематического расчета кривошипно–шатунного механизма ДВС. Построение графиков перемещения, скорости и ускорения поршня

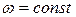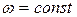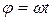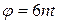Основная задача кинематического расчета состоит в определении закона движения поршня и шатуна. При этом в кинематическом расчете делается допущение, что вращение коленчатого вала происходит с постоянной угловой скоростью . Это позволяет рассчитывать все кинематические параметры механизма в зависимости от угла поворота кривошипа коленчатого вала φ, который при пропорционален времени, т.е. или (град. п.к.в.), так как
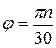(об/мин) и 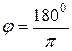(град п.к.в.).

Ниже приводится методика кинематического расчета центрального и дезаксиального кривошипно – шатунных механизмов однорядного двигателя. Аналогично выполняется расчет кинематики и динамики двигателей с V–образным расположением цилиндров, в которых применяют одинаковые шатуны, устанавливаемые рядом на общую шейку вала, а также вильчатые шатуны; отличие состоит только в условиях нагружения коленчатого вала.

Двигатели с V – образным расположением цилиндров, в которых применяют главный и прицепной шатуны, не используют на тракторах, комбайнах и автомобилях.

Кинематика центрального кривошипно – шатунного механизма.

Расчет заключается в определении кинематических параметров шатуна:

– угла отклонения ;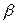

– угловой скорости качания ;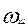

– ускорения ;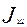

– перемещения ;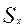

– скорости ;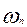

– ускорения .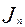

Шатун совершает переносное движение вместе с поршнем и качательное вокруг поршневого пальца. Угол отклонения шатуна 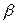от оси цилиндра определяют из соотношения треугольника АСО (рис. 2.1) на основании теоремы синусов:

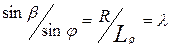(43)

откуда: .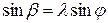

Угол 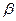считается со знаком «+», если шатун отклоняется в сторону движения кривошипа, и со знаком «–» при отклонении его в противоположную сторону. Наибольшие отклонения шатуна 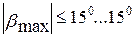будут при 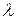, равном 90 и 270°.

Угловую скорость качания 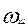и угловое ускорение 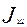шатуна определяют по формулам:

;

.

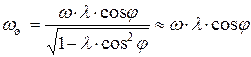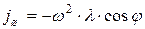При работе двигателя поршень совершает возвратно – поступательное движение, для характеристики которого определяют перемещение 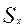, скорость 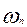и ускорение 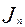. Если перемещение 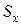поршня отсчитывается от его положения в в.м.т., то из схемы (рис. 2.1) находим:

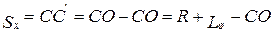
Значение 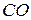определяют из треугольника :

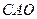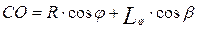CO,

откуда, следовательно: .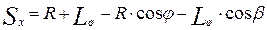

В практических расчетах эта точная формула неудобна, так как перемещение поршня зависит от двух переменных 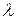и 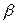. Поэтому чаще пользуются приближенной формулой, в которой переменная 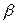выражена через 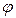на основе бинома Ньютона.

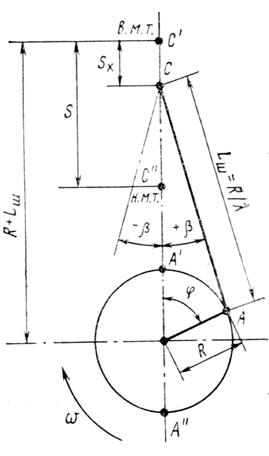
Рисунок 2.1. Схема центрального КШМ.

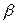– угол отклонения шатуна от оси цилиндра;

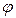– угол поворота кривошипа коленчатого вала.

При этом: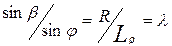

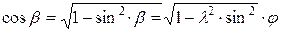
Разлагая правую часть по биному Ньютона, получим:

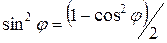
Тогда, пренебрегая вследствие малой величины членами выше второго порядка: 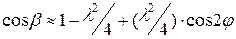и 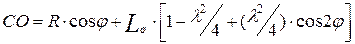или, учитывая, что 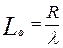, получим:

.

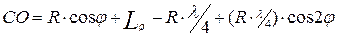Подставляя полученное выражение для 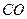в исходное уравнение, находим: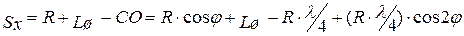

или .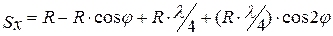

В окончательном виде после преобразований формула для расчета перемещения поршня имеет вид:

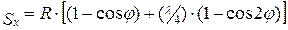
Из формулы видно, что перемещение поршня можно представить в виде суммы двух перемещений. При этом 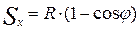– перемещение первого порядка отличается от 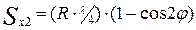– перемещения второго порядка (при положениях поршня, соответствующих п.к.в. от 0 до 90° и от 90 до 180°) на величину 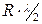, которую называют поправкой Ф.Брикса.

Физическая сущность поправки Ф.Брикса в том, что она учитывает, насколько больше перемещение поршня 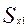при повороте кривошипа в первой четверти окружности ( 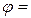0...90°), которой поршень проходит больше половины своего полного хода, по сравнению с перемещением S_xII при повороте кривошипа во второй четверти окружности ( 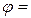90...180°), в которой поршень проходит меньше половины своего полного хода. На рисунке 2.2 представлены кривые перемещения поршня .

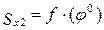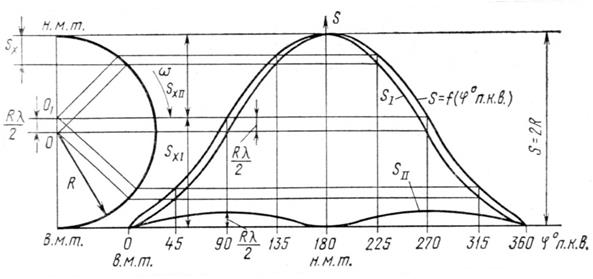
Рисунок 2.2. График перемещения поршня.

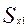– перемещение поршня при повороте кривошипа от 0 до 90°;

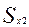– перемещение поршня при повороте кривошипа от 90 до 180°.

Скорость поршня 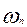определяют по формуле, которую получают дифференцированием выражения (47) по времени:

.

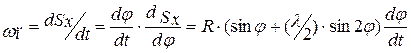Так как угловая скорость кривошипа 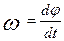то формулу можно записать в виде:

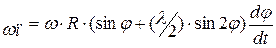
Из формулы и рисунка 2.3 видно, что скорость поршня а в.м.т. ( 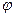= 0 и 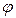= 180°) равна нулю, а при повороте кривошипа на 90 и 270° скорость поршня будет соответственно 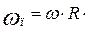и 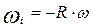, т.е. в этих точках абсолютные значения скорости поршня равны окружной скорости оси шатунной шейки коленчатого вала.

Для практических расчетов и сравнения высокооборотности (критерий подобия) двигателей используют среднюю скорость поршня:

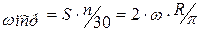
Для современных автотракторных двигателей 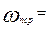5...15 м/с.

Ускорение 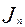поршня определяют дифференцированием выражения скорости по времени:

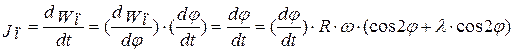
или окончательно: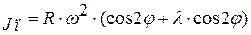

Анализ формул показывает, что скорость и ускорение поршня можно представить в виде двух составляющих. При этом первая выражает скорость и ускорение поршня при бесконечно длинном шатуне, а вторая – поправку скорости и ускорения поршня на конечную длину шатуна. Графически эти составляющие представлены на рисунках 2.3 и 2.4.

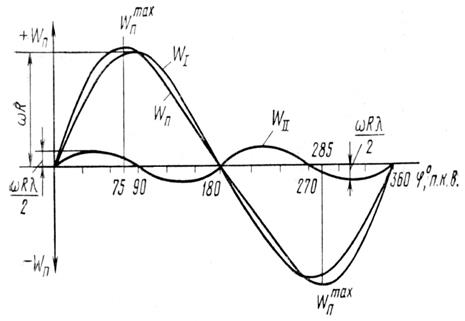
Рисунок 2.3. График скорости поршня.

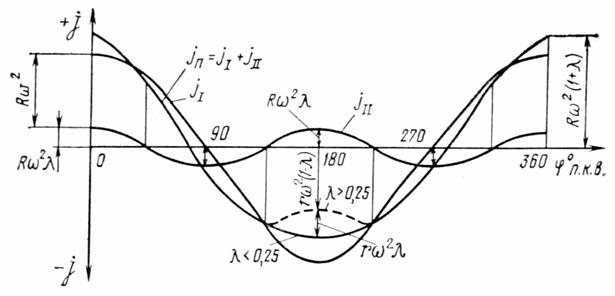
Рисунок 2.4. График ускорения поршня.

Из графиков ускорения поршня видно, что ускорение достигает максимальных положительных значений при 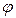= 0(360°), т.е.

,

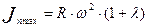Максимальное отрицательное значение ускорения поршня характерно для 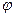=180°. При этом около н.м.т. при 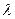<0,25 кривая ускорения выпуклая и ускорение имеет одно наибольшее отрицательное значение

,

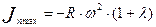а при 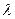> 0,25 в точке 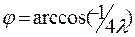кривая ускорения имеет вогнутость в сторону оси и ускорение дважды достигает максимального отрицательного значения, т. е.:

,

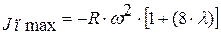Рассмотрим пример кинематического расчета двигателя Д–144.

Исходные данные: двигатель – с центральным кривошипно–шатунным механизмом; номинальная частота вращения коленчатого вала 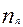=2000 об/мин; ход поршня 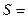120 мм; радиус кривошипа 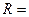60 мм; постоянная 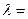0,279.

Угловая скорость кривошипа:

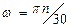=3,14·2000/30 = 209,4 с^–1.

Перемещения поршня 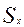, скорости поршня 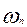, ускорения поршня 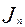, рассчитанные через каждые 10° п.к.в. по формулам сводят в таблицу.

Средняя скорость поршня: 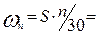0,12·2000/30 = 8

Основы динамического расчета двигателя. Силы, действующие в кривошипно–шатунном механизме ДВС. Построение развернутых диаграмм суммарных сил, действующих в кривошипно–шатунном механизме.

Во время работы двигателя детали кривошипно–шатунного механизма подвергаются действию сил давления газов в цилиндре, сил инерции движущихся масс деталей, сил трения между сопряженными деталями и сил тяжести.

Определить силы трения очень трудно, поэтому их действие учитывают механическим КПД двигателя, а при расчете деталей кривошипно–шатунного механизма силы трения не учитывают.

Силы тяжести учитывают в расчетах малооборотных двигателей ( 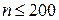об/мин), а в высокооборотных автотракторных двигателях силами тяжести деталей движения пренебрегают.

Таким образом, основные силы при расчете деталей кривошипно–шатунного механизма – силы давления, газов и инерции движущихся масс.

Силы давления газов зависят от протекания рабочего цикла, который изменяется по сложному закону и не поддается точному математическому описанию. Поэтому силы давления газов определяют по индикаторным диаграммам, полученным расчетным и экспериментальным методами.

Силы инерции зависят от массы деталей, движущихся с переменными скоростями и ускорениями. Так, например, в карбюраторных двигателях легковых автомобилей средняя скорость поршня достигает 16 м/с и ускорение 22000 м/с², в гоночных автомобилях при частоте вращения вала 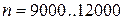об/мин ускорение поршня достигает значения 43 000 м/с² и средняя скорость поршня достигает 28 м/с. В таких двигателях силы инерции достигают больших значений. Силы инерции движущихся масс разделяют на силы инерции возвратно–поступательных масс 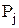, действующие вдоль оси цилиндра, и на силы инерции вращающихся масс, которые называют центробежными силами 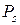.Силы 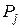через поршневой палец передаются на подшипники коленчатого вала, корпус двигателя, вызывая при этом вибрации в направлении оси цилиндра, а 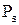действуют в плоскости вращения кривошипа коленчатого вала и также вызывают вибрации двигателя. В многоцилиндровых двигателях от сил инерции 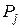и центробежных сил 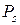возникают моменты, которые передаются на корпус и опоры двигателя. Стремление уравновесить или уменьшить их действие на опоры приводит к дополнительному нагружению коленчатого вала и корпуса двигателя.

Эффективный момент, создаваемый в двигателе, передаётся к потребителю энергии, но при этом возникает равный по значению и противоположный по направлению реактивный момент, действующий на корпус в плоскости, перпендикулярной коленчатому валу, вызывая его колебание. Ниже рассматриваются основы динамического расчета двигателя Д–144. При этом приводится определение сил давления газов, сил инерции, суммарных сил, действующих в кривошипно–шатунном механизме, неравномерности вращения коленчатого вала.

Силы давления газов на поршень.

В результате сгорания топлива в цилиндре двигателя образуются газы, давление от которых воспринимается поршнем, стенками и головкой цилиндра. Под действием давления возникают силы давления газов. Для упрощения расчетов их заменяют одной силой. Сила давления газов 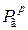(рис. 2.4.а) действует на поршень, направлена вдоль оси цилиндра, передается коленчатому валу и через него – на картер двигателя. Другая сила 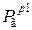действует на головку цилиндра, равна по значению 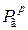,направлена в противоположную сторону и через шпильки крепления головки цилиндра также перелается на картер двигателя. Такимобразом эти силы взаимно уравновешиваются и на опоры двигателя не действуют. Внешние силы давления газов в двигателе проявляются в виде крутящего 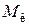и опрокидывающего (обратного) 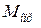моментов.

Их определение будет рассмотрено позже.

Закон изменения давления газов в цилиндре в функции угла поворота коленчатого вала 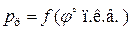задастся индикаторной диаграммой, полученной экспериментально или построенной по данным теплового расчета.

Так как на поршень с внутренней полости картера действует атмосферное давление, то избыточное давление газов на поршень определяют из выражения:

,

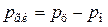где 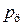– текущее абсолютное давление газов в цилиндре (определяют из индикаторной диаграммы), МПа; 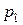– давление окружающей среды (принимают равным 0.1 МПа при нормальных условиях).

Тогда сила от давления газов 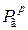на поршень:

,

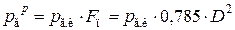где 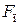– площадь поршня, 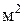; D –диаметр цилиндра, м.

Расчетную силу давления газов 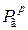, действующую на поршень, переносят на ось поршневого пальца и раскладывают на две составляющие:

– силу 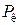,направленную по оси шатуна, которая сжимает или растягивает стержень шатуна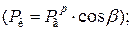

– силу 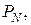перпендикулярную оси цилиндра, которая прижимает поршень к поверхности цилиндра ( 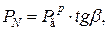где 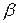– угловое перемещение шатуна).

Силы инерции, действующие в центральном кривошипно–шатунном механизме.

В кривошипно–шатунном механизме поступательное движение совершает комплект поршня (поршень, палец, кольца, верхняя головка шатуна), вращательное движение совершает кривошип коленчатого вала и нижняя головка шатуна, сложное плоскопараллельное – стержень шатуна. Массы этих деталей при движении образуют силы инерции, которые создают дополнительную нагрузку, и их необходимо учитывать при расчетах.

Для упрощения расчета действительный кривошипно–шатунный механизм заменяют динамической моделью. В ней массы деталей отождествляют с системой условных масс, сосредоточенных (приведенных) в определенных точках механизма, законы движения которых известны.

Массу комплекта поршня 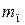условно считают сосредоточенной на оси поршневого пальца в точке С. Там же сосредоточена часть массы шатуна 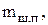которую принимают равной .

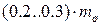На оси шатунной шейки в точке А сосредоточены масса нижней части шатуна 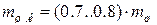, масса шатунной шейки 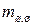и масса средней части двух щек кривошипа 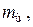центр тяжести которых находится на радиусе .

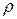На оси коренной шейки в точке О сосредоточена масса коренной шейки 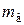и часть массы щек; они расположены симметрично относительно оси вращения, поэтому считаются уравновешенными и при расчетах не учитываются.

В результате получаем систему сосредоточенных масс, динамически эквивалентную кривошипно–шатунному механизму двигателя:

– масса, совершающая возвратно–поступательное движение, сосредоточена в точке С:

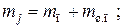
– масса, совершающая вращательное движение, сосредоточена в точке А:

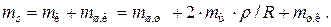
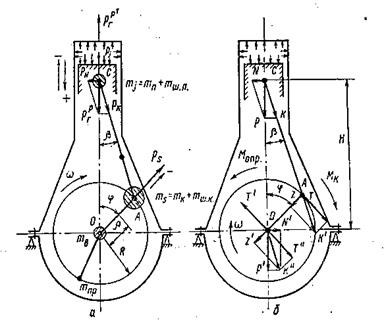
а – силы давления газов и силы инерции; б – суммарные, силы, действующие в звеньях и подшипниках коленчатого вала.

Рисунок 2.4. Силы и моменты, действующие в центральном кривошипно–шатунном механизме

При расчете 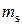в V–образном двигателе с центральными шатунами необходимо значение 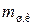удвоить, так как на одной шейке установлены два шатуна.

Значение масс 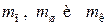принимают по данным двигателей прототипов, подсчитывают по чертежам, определяют взвешиванием и другими методами.

Таким образом, с учетом приведенных масс и рассмотренных ранее ускорений в кривошипно–шатунном механизме действуют две силы инерции:

– сила инерции от возвратно–поступательных масс:

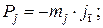
– центробежная сила инерции от вращающихся масс:

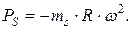
После подстановки в уравнение нахождения сил инерции от возвратно–поступательных масс значения ускорения j_п, которое определяли ранее в кинематическом расчете по формуле 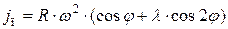, получаем:

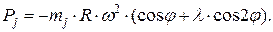
Для удобства анализа силу инерции 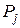раскладывают на две силы:

– силу инерции первого порядка:

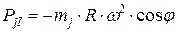
и силу инерции второго порядка:

.

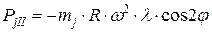Сила 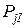изменяется по закону косинусоиды, 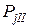– по закону косинуса двойного угла. Период изменения 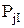составляет один оборот коленчатого вала (360° п.к.в.), а 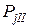– пол–оборота (180° п. к. в.).

Абсолютное значение силы инерции второго порядка 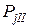в 3.5..4.5 раза меньше силы инерции первого порядка, так как в уравнение определения силы 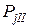входит .

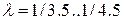Знак «–» в уравнениях показывает, что действие сил инерции противоположно направлению действия ускорения. Сила инерции 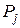действует по оси цилиндра, как и сила давления газов 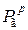, положительна, если направлена к оси коленчатого вала, и отрицательна, если от оси.

Центробежная сила инерции 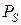всегда постоянная по значению (так как 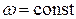), действует по радиусу кривошипа, всегда отрицательная, так как направлена от оси коленчатого вала.

Суммарные силы, действующие в центральном кривошипно–шатунном механизме.

Приведенный ранее анализ сил, действующих в кривошипно–шатунном механизме, показывает, что при расчете нагрузок на детали двигателя необходимо учитывать совместное влияние сил давления газов и сил инерции, которые изменяются в зависимости от угла поворота коленчатого вала.

Суммарную силу Р, действующую на поршень, определяют алгебраическим сложением силы давления газов 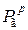и силы инерции поступательно движущихся масс :

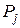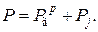
Суммарная сила будет действовать по оси цилиндра и приложена на оси поршневого пальца в точке С.

Для определения сил, действующих в деталях кривошипно–шатунного механизма, разложим силу Р на составляющие:

– силу N,направленную перпендикулярно оси цилиндра (нормальную силу) и прижимающую поршень к стенке цилиндра:

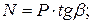
– силу, направленную по оси шатуна, которая сжимает или растягивает шатун:

.

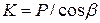От действия силы К через шатун на шатунную шейку коленчатого вала возникают силы:

– радиальная Z , действующая по радиусу кривошипа:

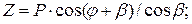
– тангенциальная Т, направленная по касательной к окружности радиуса кривошипа R:

.

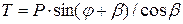Если радиальную силу Zперенести в центр О коренной шейки (сила 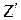) и приложить две взаимно уравновешенные силы 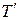и 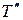, параллельные и равные силе Т, то в результате получим пару сил Т и 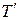, которая приводит во вращение коленчатый вал. Момент этой пары называют крутящим моментом 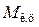двигателя данного цилиндра:

.

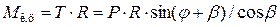Если также сложить оставшиеся силы 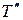и 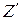, то получим равнодействующую 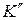, равную силе К, которую можно разложить на составляющие 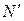и 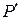. Анализируя действие сил 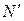и N, устанавливаем, что они образуют пару сил, момент которой называют опрокидывающим (обратным) моментом 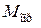. Он всегда равен крутящему моменту, но противоположен по направлению:

,

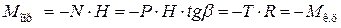где H – расстояние между осями поршневого пальца и коренной шейки.

Сила 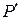равна силе 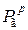и уравновешивается силой давления газов, приложенной к головке цилиндра, а сила инерции 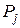остается свободной (неуравновешенной) и действует на опоры двигателя. К центру шатунной шейки кривошипа приложена центробежная сила 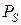, направленная вдоль кривошипа в сторону от оси коленчатого вала; она также не уравновешена и через коренные подшипники передается на опоры двигателя. По результатам решения уравнений строят развернутые диаграммы изменения суммарных сил P, N, K, T и Z в зависимости от угла поворота кривошипа коленчатого вала.

Уравновешивание двигателей внутреннего сгорания

Различают внешнюю и внутреннюю неуравновешенности поршневых двигателей внутреннего сгорания.

Внешняя неуравновешенность – это наличие периодических сил инерции и моментов сил инерции, а также опрокидывающего момента, которые передаются на опоры двигателя и далее – на раму трактора, комбайна, автомобиля или на фундамент (для стационарного двигателя).

Внутренняя неуравновешенность – это возникновение под действием воспринимаемых двигателем нагрузок в поперечных сечениях блока цилиндров перерезывающих сил, а также моментов упругих сил, которые называют внутренними изгибающими моментами и внутренними скручивающими моментами.

Расчет 'внутренних сил и моментов применяют для оценки деформаций блока цилиндров, а также возникающих в нем напряжений и вибраций.

Ниже будет рассматриваться только внешняя неуравновешенность двигателей.

При работе поршневых ДВС возникают силы давления газов, силы инерции поступательно движущихся масс, центробежные силы инерции вращающихся масс, моменты от этих сил, а также крутящий и опрокидывающий моменты. В двигателях уравновешивается только сила давления газов, действующая на головку цилиндров и через коренные подшипники на остов двигателя. Остальные силы и моменты, непрерывно изменяясь по значению и направлению, передаются на опоры двигателя, далее на подмоторную раму и всей машине. В результате детали, сборочные единицы и агрегаты совершают колебательные движения. При этом возникают вибрации, снижающие эффективную мощность и топливную экономичность (примерно до 5%), вследствие затраты энергии на возбуждение вибрации и дополнительные механические потери; ослабляются крепления агрегатов и деталей, что вызывает нарушение соосности валов двигателя и потребителя и ускоряет износ деталей; нарушаются регулировки и затрудняются наблюдения за показаниями контрольно–измерительных приборов и снижается их надежность; повышается утомляемость обслуживающего персонала. Поэтому уменьшение влияния переменных сил и моментов, действующих на двигатель, относится к числу основных требований, предъявляемых к двигателям внутреннего сгорания.

Уравновешенность – это такое состояние двигателя, при котором на установившемся режиме работы на его опоры передаются постоянные по значению и направлению силы и моменты.

Условие полной конструктивной уравновешенности двигателей выражается системой уравнений:

.

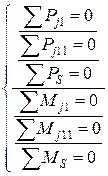При разработке конструкции двигателей стремятся к тому, чтобы уменьшить влияние свободных сил и моментов. Для этих целей применяют следующие конструктивные мероприятия: выбор соответствующего числа и расположения цилиндров и схемы расположения кривошипов, установку простейших противовесов и сложных уравновешивающих механизмов.

Создание конструктивно предусмотренной уравновешенности двигателя достигается выполнением соответствующих требований при производстве деталей, их сборке и регулировке, а также при ремонте и эксплуатации двигателей. При этом обращают внимание на:

– соблюдение допусков на массы и размеры поршней, шатунов, коленчатого вала и других деталей;

– проведение статической и динамической балансировки коленчатого вала;

– достижение идентичности протекания рабочего процесса во всех цилиндрах за счет одинакового их наполнения, одинаковых степеней сжатия во (всех цилиндрах, одинаковой регулировки зажигания или впрыскивания топлива по цилиндрам, идентичного теплового режима и т. д.

Эти мероприятия относятся к условиям как производства, так и ремонта двигателей. Таким образом, уравновешивание – это комплекс конструктивных, производственных и эксплуатационных мероприятий, направленных на уменьшение или полное устранение неуравновешенных свободных сил инерции и моментов.

Расчет динамического уравновешивания многоцилиндрового двигателя заключается в определении значений и направления действующих неуравновешенных сил и моментов сил инерции, которые необходимо в дальнейшем уравновесить с помощью наиболее простых конструктивных мероприятий.

При расчете сил и моментов сил инерции используют выражения:

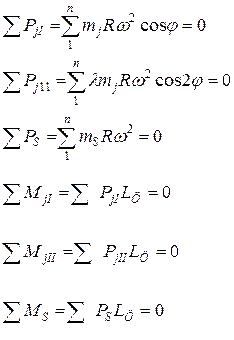
где 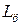– расстояние между осями цилиндров; 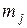и 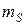– неуравновешенные массы поступательно движущихся и вращающихся частей кривошипно–шатунного механизма одного цилиндра.

На основании расчета динамического уравновешивания двигателя можно сделать заключение о его уравновешенности для конкретных условий применения.