Гипотеза сплошности газовой среды

Теория была введена в практику исследования Даламбером в 1744 году, а затем Эйлером в 1753 году в противовес корпускулярной теории Ньютона.

Воздух атмосферы представляет собой смесь различных газов. До принятия гипотезы сплошности исходили при экспериментах из того, что существует как бы смесь несвязанных между собой молекул газов, между которыми существуют дыры (сито).

Гипотеза сплошности в аэродинамике основана на том, что расстояние между молекулами воздуха и свободный пробег молекул малы по сравнению с обтекаемым воздухом телом. В связи с этим принимается, что воздух (и вода) однородная, сплошная, без разрывов масса [17, 19, 20].

Длина свободного пробега молекул зависит от числа молекул в единице объема, т.е. от плотности среды. Мы уже знаем, что вся масса воздуха находится в пределах тропосферы (высота Н ≤ 10…17 км) и что плотность сильно уменьшается с ростом высоты над уровнем моря. У Земли (Н = 0) в одном кубическом миллиметре содержится 2,7∙10⁺¹⁶ молекул воздуха при массовой плотности ρ_о ≈ 0,125 кг∙с²/м⁴. На высоте Н = 160 км в том же объеме содер-

жится 1 молекула воздуха. А плотность воздуха, например, на высоте Н = 20 км, ρ₂₀ = 0,008965 кг∙с²/м⁴.

Длина свободного пробега по высотам в среднем распределяется следующим образом (таблица 2.2).

Таблица 2.2

Некоторые ученые считают границей применимости гипотезы сплошности отношение длины свободного пробега молекулы воздуха к хорде крыла, равное 1/10⁺⁵.

Кроме плотности воздуха длина свободного пробега зависит от температуры (т.е. от скорости хаотического движения) и от размеров молекул. Средняя длина пробега молекул воздуха рассчитывается по формуле

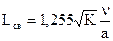, (2.4)

где К – отношение теплоемкости воздуха при постоянном давлении с_р к его теплоемкости при постоянном объеме с_v, т.е.

;

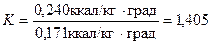ν – кинематический коэффициент вязкости, м²/с; a – скорость звука в воздушной среде в м/с.

Так как параметры ν и a зависят от высоты над уровнем моря, то и параметр L_св зависит от той же высоты (см. таблицу 2.2).

Критерием применимости гипотезы сплошности является число Кнудсена

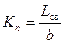или 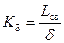, (2.5)

где b – хорда крыла, δ – толщина пограничного слоя.

Окончательно, или другое значение коэффициента Кнудсена таково:

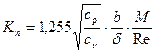, (2.6)

где М – число Маха, Re – коэффициент Рейнольдса, равный

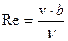, (2.7)

где v – скорость движения в м/с, b – средняя хорда крыла в метрах, ν – коэффициент кинематической вязкости в м²/с (рис. 2.1).

Практический смысл гипотезы сплошности для специалистов в области приборостроения и самолетостроения состоит с возможности определения границ применения способов измерения воздушных параметров, например, манометрического метода при определении скорости, числа М, подъемной силы.

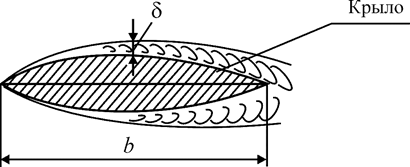
Рис. 2.1. Обтекание крыла потоком воздуха

По Ньютону получалось в его корпускулярной теории, что сопротивление движению есть результат ударов частиц о тело и равно:

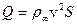, (2.8)

где ρ_∞ – плотность воздуха; v – скорость движения; S – площадь крыла.

Теперь мы уже будем знать, что формула неверна, она завышает силу сопротивления в два раза.

Область аэродинамики, рассматривающая движение твердых тел в сильно разреженном газе, называется супераэродинамикой [17].

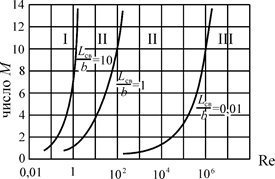
Рис. 2.2. Границы областей аэродинамики и супераэродинамики: I – Область супераэродинамики (потоки свободных молекул); II – Переходная область – течение со скольжением (вместо полного торможения); III – Область аэродинамики (газовой динамики, обычные потоки газа с большими скоростями)

Выводы из гипотезы сплошности:

Гипотеза упрощает исследование процессов движения.

Она позволяет рассматривать все механические характеристики жидкой среды – скорости, плотности, давления, числа М и т.д., как функции координат точки и времени. Эти функции предполагаются непрерывными и дифференцируемыми.

Из гипотезы сплошности следуют ограничения применимости методов измерения скоростных параметров. Например, манометрический метод может быть достоверно использован при Н ≈ 30000 метров над уровнем моря, при скоростях, соответствующих числу Re = 10²…10⁷.

При большом разряжении воздуха и при несоблюдении критерия Кнудсена воздушную среду нельзя считать сплошной. В этих условиях нельзя считать применяемым и принцип непрерывности течения потока воздуха. В этих условиях иными становятся законы образования силы сопротивления движению и подъемной силы. В свободномолекулярном потоке газа единственными силами воздействия газовой среды на движущееся тело являются силы ударов молекул газа о поверхность тела. Величину аэродинамических сил можно оценить по ударной теории Ньютона.