Особенности пластического деформирования при переменных температурах

Рассмотрим некоторые понятия и приемы, используемые в рас­четах сварочных деформаций и напряжений, связанные с протека­нием пластических деформаций.

Рассмотрим одноосное нагружение с использованием схематизированных диаграмм предел текучести — температура (рис.7) в предположении, что модуль упругости Е и коэффициент Пуассона μ постоянны во всем диапазоне рассматриваемых температур, а материал — идеальный упругопластический.

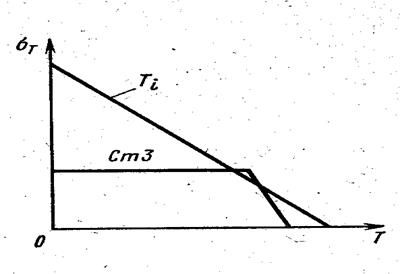
Рис. 7 Схематизированные зависимости пре­дела текучести от температуры

для СтЗ и ти­тана

Пусть известен ли­нейный закон изменения собственной деформации ε укорочения (сжатия) при повышении температуры стержня (рис. 8, а). Та­кое изменение деформаций от температуры возможно в стержне, который жестко заделан по концам. Изобразим изменение дефор­мации ε_т, соответствующей пределу текучести σ_т для низкоуглеродистой стали ε_т =σ_т/Е. До точки А абсолютное значение ε будет меньше σ_т. Никаких пластических деформаций на этом участке возникать не будет, напряжение в стержне σ=-εЕ. В точке А напряжения достигнут σ_т и будут равны ему в дальнейшем при повышении температуры. Отрезки CD и C'D^', соответствующие разным стадиям нагрева, будут выражать упругую составляю­щую, a DF и D'F' — пластическую составляющую деформации

ε = ε_упр + ε_пл (14)

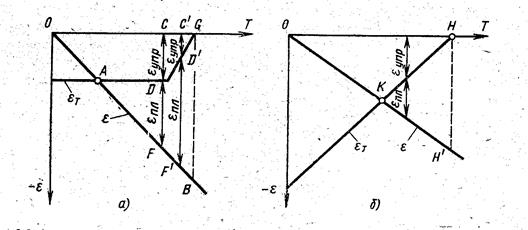
Рис. 8 Упругие и пластические деформации в стержне и при его нагреве

При достижении точки В окажется σ_т=0, ε_упр=0. В области более высоких температур за точкой В вся деформация будет пластической. .

В случае титанового сплава (рис. 8,6) пластические дефор­мации возникнут только после достижения точки К. В точке Н' деформация ε_упр=0.

Рассмотрим диаграмму деформирования стального стержня, прикрепленного по концам к двум абсолютно жестким стенкам (рис. 9,а). Пусть коэффици­ент линейного расширения и модуль упругости не зависят от температуры. На стадии на­грева собственная деформация будет равна температурной де­формации αТ с обратным знаком. В стержне будут происходить те же явления, которые рассмотрены на рис. 9, а.

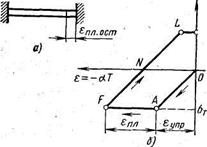
Рис.9 Диаграмма изменения на­пряжения (б) при нагреве и

охлаждении стержня, закрепленного жестко по концам (а)

Пусть стер­жень нагревался только до точки F, а затем началось его остывание. В точке А (рис. 9, б) напряжения стали равными —σ_т. Пос­ле начала остывания от точки F напряжения будут уменьшаться. При некоторой температуре в точке N они станут равными нулю, а в процессе дальнейшего остывания появятся напряжения растяжения, так как стержень жестко закреплен по концам. В точке L напряжения достигнут предела текучести при растяжении и нач­нется снова пластическая деформация, но уже удлинения (растя­жения), а не укорочения (сжатия), как было на стадии нагрева OAF. Отрезок AF выражает пластическую деформацию укороче­ния, а отрезок LM — пластическую деформацию удлинения. Если к отрицательной величине AF прибавить положительную LM, то получим остаточную пластическую деформацию укорочения (см.рис.9,а).

ε_пл.ост = ε_{пл.нагр} + ε_{пл.остыв.} (15)

Остаточную деформацию можно также получить, если взять разность абсолютных значений пластических деформаций

|ε_пл.ост| = |ε_{пл.укор}| + |ε_пл.удл.| (16)

Остаточная пластическая деформация укорочения является при­чиной остаточных растягивающих напряжений, соответствующих точке М. Если стержень отсоединить от жесткой стенки, то он со­кратится на величину ε_пл.ост.

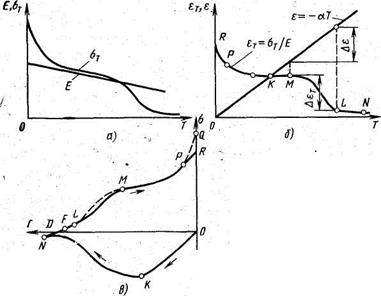
Разберем более сложный случай нагрева и охлаждения закреп­ленного жестко стержня, у которого с изменением температуры меняются по произвольному закону σ_т и Е (рис. 10,б).

Рис. 10 К определению на­пряжений и деформаций в стержне из материала, пре­дел текучести и модуль уп­ругости которого зависят от температуры:

а — зависимость σ_т и Е от тем­пературы: б — зависимость ε_Т от температуры; в — диаграм­ма изменения напряжения в стержне в процессе его нагрева и охлаждения

Примем, что при пластической деформации металл ведет себя как идеальный упругопластический. На рис. 10, б прямая ε показывает рост собственной деформации, равной температурной деформации αТ с обратным знаком, т. е. ε=- αТ . Для удобства сравнения с по­ложительной величиной σ_т=σ_т/Е линия ε=—аТ отложена в по­ложительной области. В точке К собственная деформация |ε| до­стигнет величины ε_т =σ_Т /Е, и с этого момента начнется пластическая деформация. Во время дальнейшего нагрева пластическая деформация будет протекать, если выполняется условие

|∂ε/∂Т| > |∂ε_Т/∂T| (17)

Из характера кривой ε_т (см. рис. 10, б)видно, что ∂ε_Т/∂T<0 , a ∂ε/∂Т >0. Поэтому пластическая деформация будет протекать в течение всего периода нагрева. Пусть в точке N нагрев прекра­тился и началось охлаждение, тогда знак приращения температур­ной деформации изменится на противоположный.

Для более, наглядного представления характера изменения на­пряжений и процесса протекания пластической деформации рассмотрим диаграмму на рис. 10, в. Исследуем, стадию нагрева и ох­лаждения в случае жестко заделанного стержня. Участок ОК соответствует упругой стадии роста напряжений сжатия вследствие расширения стержня при нагреве. Непрямолинейность линии ОК вызвана уменьшением модуля упругости при повышении темпера­туры. Участок KN повторяет кривую зависимости σ_т от темпера­туры. От точки N после начала остывания напряжения сжатия начнут уменьшаться, перейдут через нулевые значения в точке D, а в точке F достигнут σ_т. Затем от точки F начнется пластическая деформация удлинения. Она будет происходить до тех пор, пока выполняется условие |∂ε/∂Т| > |∂ε_Т/∂T| или, что то же самое, в случае α=const, α>|∂ε_Т/∂T|. Для конкретных кривых на рис. 10 это условие перестанет выполняться в точке L (см. рис. 12, б). В дальнейшем рост собственной деформации будет ид­ти в соответствии с ростом αΔT, а напряжения будут возрастать по некоторой сплошной кривой LM, в то время как рост σ_т будет следовать в соответствии с штриховой линией LM (см рис. 10, в). В некоторой точке М приращение собственной деформации Δε в интервале LM (см. рис. 10, б) достигнет по значению прираще­ния деформации предела текучести Δε_т в том же интервале LM, и пластическая деформация начнется снова: Δε= Δε_т.

Следует отметить, что прекращение пластической деформации зависит от условия (17), в то время как ее начало определяется абсолютным значением упругой деформации, которая должна достичь ε_Т. Пластическая деформация будет продолжаться до точки Р, где снова перестанет выполняться условие |∂ε/∂Т| > |∂ε_Т/∂T|. В дальнейшем, вплоть до полного остывания, напряжения будут возрастать по сплошной линии PR, в то время как уровень σ_т, бу­дет следовать по штриховой линии PQ.

Скорость изменения ∂ε_пл/∂Тможно найти, если учесть, что ε_т является упругой составляющей собственной деформации, т. е.

ε = ε_упр + ε_пл = ε_т + ε_пл (18)

Дифференцируя по Т выражение (18), получим

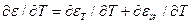
Тогда

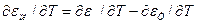(19)

Уравнение (19) справедливо только в случае протекания пластических деформаций.