Деформации, напряжения и перемещения при сварке

Деформации металла при сварке.Одной из основных причин появления сварочных деформаций является расширение и сокра­щение металла при нагреве и остывании. Если материал изотро­пен, а коэффициент линейного расширения металла aво всех точ­ках тела одинаков, то независимо от формы тела при равномер­ном его нагреве от нуля градусов до температуры Т возникнут во всех направлениях одинаковые температурные деформации e = aТ:

e_x = e_y = e_z = aТ (1)

Абсолютное изменение размера L по любому направлению со­ставит

DL= aТL (2)

При этом, как известно, не будет возникать каких-либо напря­жений, вызванных расширением тела. Не будут возникать напря­жения в теле и в том случае, если изменение температур по любо­му направлению следует линейному закону. После остывания тела все его размеры вернутся к первоначальным значе­ниям, которые они имели до нагрева.

В случае неравномерного нагрева в теле возникают такие температурные деформации, которые должны были бы вызвать в нем разрывы или надавливание частиц друг на друга. На самом деле возникают лишь напряжения, создающие необходимые для сохранения сплошности тела упругие де­формации e_уп. Если напряжения превосхо­дят соответствующее значение, то возникают также и пластические деформации e_пл. При достижении напряжениями разрушающего уровня возникают трещины.

Вследствие появления упругих и пластических деформаций из­менение размеров частичек тела не будет следовать закону рас­пределения температурных деформаций e_a. Возникающие дефор­мации, которые можно наблюдать и измерить, в теории упругости и пластичности называют просто деформациями, не присваивая им никаких дополнительных определений. В литературе по сварке под словом деформации часто понимают также искажения форм конст­рукций. В настоящей курсе возникающие в теле деформации называются наблюдаемыми деформациями. В отдельных работах их называют деформациями формоизменения или внешними деформациями. Ес­ли тело изотропно и коэффициенты a во всех направлениях равны, то наблюдаемые деформации в направлении осей Ox, Oy, Oz бу­дут равны сумме упругих, пластических и температурных дефор­маций:

e_н = e_упр + e_пл + e_a (3)

Сдвиговые наблюдаемые деформации при этом не будут со­держать температурной составляющей деформации

g_н = g_упр + g_пл (4)

В случае неодинаковых коэффициентов линейного расшире­ния a₁ и a₂ по двум осям 1 и 2 деформации g_н также, будут зависеть от a₁ и a_2. Если к телу не приложены никакие нагрузки, то деформации (e_упр + e_пл) и (g_упр + g_пл) называют собственными деформациями, или, иногда, внутренними. Последнее название, вероятно, менее удачно.

Кроме температурных деформаций в теле могут возникать так­же и деформации, вызываемые различными структурными превра­щениями, которые обычно происходят с увеличением или умень­шением объема тела. Формально деформации от структурных пре­вращений можно рассматривать как частный случай температур­ных деформаций и приравнивать к некоторому дополнительному нагреву или охлаждению тела. Формулы (3) и (4) получены из предположения, что первоначально тело находится в естественном ненапряженном состоянии. Но в теории сварочных деформаций возможны случаи, когда еще в исходном состоянии в теле имеются начальные деформации, например, вызванные предшествующими пластическими деформациями. Тогда формулы (3) и (4) пре­образуются к виду

e_н = e_упр + e_пл + e_a + e_пл,0 (3,а)

g_н = g_упр + g_пл + g_пл,0 (4,а)

В этом случае e_пл и g_пл означают дополнительные пластиче­ские деформации, которые возникли при протекании какого-либо процесса, начиная от исходного состояния. Конечное суммарное значение пластических деформаций может быть получено, если к на­чальным пластическим деформаци­ям e_пл,0 и g_пл,0 добавить возникшие дополнительно пластические дефор­мации e_пл и g_пл , т. е. будем иметь (e_пл,0 + e_пл ) и (g_пл,0 + g_пл ).

Рассмотрим на примере стержня с пружиной (рис. 1) некоторые характерные случаи образования деформаций. Допустим, стер­жень нагрет и должен был бы удлиниться до точки В. В дей­ствительности он удлинится только до точки А, так как пружина будет оказывать на стержень давление. Согласно (3) e_н будет иметь положительное значение, но так как e_н < e_a, то (e_упр+e_пл) окажется отрицательной. Из этого примера следует, что удлинение стержня, происходящее в условиях одновременного изменения температуры, еще не означает, что в нем возникли напряжения растяжения. В данном примере в стержне, несмотря на его удли­нение, возникают напряжения сжатия.

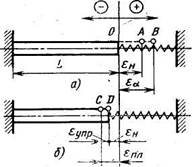
Рис. 1 Деформация стержня при его на­греве (а) и охлаждении (б)

Допустим, что при нагреве стержня возникла пластическая де­формация e_пл. Она будет отрицательной величиной. При остыва­нии стержень будет сокращаться и при отсутствии пружины дол­жен был бы сократиться до точки С (рис. 1,б). Но из-за натя­жения пружины стержень займет положение D и будет находить­ся в растянутом состоянии. При этом возникнет e_упр положитель­ного знака, в то время как e_пл и e_н будут отрицательными. Так как после полного остывания e_a =0, то

e_н = e_упр + e_пл (5)

Деформации могут быть временными и остаточными. Времен­ными деформациями будем называть такие, которые существуют в теле в период протекания какого-либо процесса (нагрева, осты­вания, структурного превращения); остаточными — деформации, которые сохраняются в теле устойчиво в течение продолжительного периода времени после завершения какого-либо процесса.

Напряжения.Напряжения, существующие в теле, связаны оп­ределенными зависимостями с упругими деформациями. Рассуждая формально, можно было бы описать деформированное состояние тела только, через компоненты деформаций, не прибегая к напря­жениям. Однако оценка состояния тела через напряжения оказы­вается удобной, особенно если рассматриваются вопросы, связан­ные с прочностью.

Напряжения, как и деформации, могут быть классифициро­ваны по следующим, признакам: по причинам, их вызвавшим; по периоду времени существования; по степени многоосности; по объ­емам, в которых они взаимно уравновешены. В табл. 1. дана та­кая классификация.

σ_x= 2Gε_x + λΔ, τ_xy= Gγ_xy,

σ_y= 2Gε_y + λΔ, τ_yz= Gγ_yz, (6)

σ_z= 2Gε_z + λΔ, τ_xz= Gγ_xz,

где G – модуль сдвига, а λ=2μG/(1-2μ).

Таблица 1