Информационные процессы

Арифметико-логические основы ЭВМ

В основе любой научно-технической, биологической и социальной системы управления и функционирования, а тем более в основе систем вычислительной техники, лежат информационные процессы, связанные со сбором и обработкой информации, ее передачей, хранением, распределением, отображением, регистрацией, считыванием и т.д. Из всех перечисленных информационных процессов в итоге можно выделить четыре основных процесса или процедуры: приеминформации, передача, хранение и ееобработка. Реализация всех этих процедур в общем случае сопровождается преобразованием физического носителя информации и формы ее представления.

Информация - понятие очень емкое и трудно поддающееся четкому определению. Не останавливаясь на сложной проблеме строгого фор-мализованного и полного определения понятия информации, примем, что информация есть сведения о тех или иных явлениях или объектах, точнее - сведения об определенных свойствах или параметрах этих явлений или объектов и о зависимостях между этими свойствами. Информация воплощенная и зафиксированная в некоторой материальной форме, называется сообщением, а физическое средство передачи соощения - сигналом. Или иначе: сигнал - это процесс изменения во времени некоторого физического параметра s(t) какого-либо объекта, служащий для отображения, регистрации и передачи сообщения.

Характер изменения сигнала во времени может быть представлен графически, в виде осциллограмы, посредством таблицы, в которую вносятся значения siв i-тые моменты времени; сигнал также может быть описан аналитически.

Для того, чтобы сделать сигнал объектом теоретического изучения и расчетов используют те или иные способы математического его описания, т.е. создают математическую модель сигнала. Причем, при создании такой модели описываются только те свойства сигнала, которые представляются объективно важными и игнорируется большое число второстепенных признаков.

В качестве математической модели сигнала может быть принята, на-пример, функциональная зависимость, аргументом которой является время:

s = f(t). Причем при такой модели имеется в виду, что причиной изменения величины s является не само время, а некоторая другая физическая величина. Поэтому точнее говорить, что обозначая сигнал через s(t), q(t),... принимается модель, описывающая изменение величин s, q,... во времени.

Существуют различного типа сигналы: непрерывные, т.е. аналоговые, сигналы дискретные, квантованные, кодированные (цифровые), модулированные, импульсные и т.д.

Как уже отмечалось, практически при любой обработке информации осуществляются те или иные преобразования сигналов. Преобразования сигналов, в частности, применяются при изменении носителя информации или самой передаваемой функции по определенному закону, обеспечивающему однозначное соответствие между входной функцией и выходной.

В случае непрерывного входного сигнала чаще всего первой процедурой изменения типа сигнала является его дискретизация.

Дискретный сигнал описывается решетчатой функцией (последова-тельностью, временным рядом) X(nt), в которой величина X может принимать любые значения в некотором интервале [X', X"], в то время, как независимая переменная n принимает только дискретные значения n = 0, 1, 2,... t - интер-вал (шаг) дискретизации. Дискретизация непрерывного сигнала s(t) может производиться во времени или по уровню (параметру). Последний случай дискретизации обычно называется квантованием по параметру и он будет рассмотрен отдельно.

Когда дискретизация сигнала s(t) осуществляется во времени, то не-прерывный сигнал s(t) заменяется (представляется) последовательностью импульсных сигналов, амплитуда которых соответствует значениям непрерывного сигнала в дискретные моменты времени nt. В данном случае значение t равно временному интервалу между смежными отсчетами. Тогда fD = 1/t - это циклическая частота дискретизации, а D = 2fD соответствующая круговая частота.

Примем, что сигнал s(t) задан или графически или же таблично, в котору. внесены его значения в пределах периода времени Т через определенные равные интервалы времени, т.е. период Т разделен в этом случае на 2n равных частей (рис.1.1.). Тогда абсциссы точек разбиения будут равны:

tk = (kT)/2n, а ординаты в этих точках:

sk = f(tk ), где k=0,1,2,...,2n.

Здесь sk значение амплитуды сигнала s(t) в k-тый момент времени.

Если для непрерывного сигнала действительно следующее выражение:

s(t) = Smsint, то после дискретизации во времени этот сигнал описывается уравнением:

s(nt) = Smsin nt.

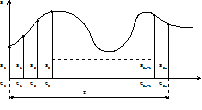
Рис. 1.1. Кривая квантования.

В результате дискретизации исходная функция s(t) заменяется совокупность. отдельных значений sk, по которым можно восстановить исходную функцию s(t) с некоторой погрешностью. Функцию, полученную в результате такого восстановления (интерполяции) называют воспроизводящей. Для представления воспроизводящей функции наиболее часто используются степенные алгебраические полиномы вида

,

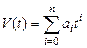где n - степень полинома, ai - действительные коэффициенты.

При дискретизации сигналов приходится решать вопрос о том, как часто следует производить отсчеты функции, т.е. каков должен быть шаг дискретизации.

Согласно теореме В.А.Котельникова, если функция s(t) не содержит частот выше некоторой Fm, то она полностью определяется своими мгновенными значениями в моменты времени, отстоящими друг от друга на величину

1/(2Fm ), т.е.

,

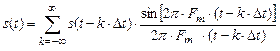где k - порядковый номер отсчета функции; t = 1/(2Fm) - шаг дискретизации по времени,sk = s(tk) - мгновенные значения сигнала s(t) в k-ой отсчетной точке tk = k/m = k/(2Fm) = kt.

Из этой теоремы следует, что для однозначного представления функции с ограниченным спектром на интервале времени Т достаточно иметь некоторые n значений этой функции, где

n = T / t = 2FmT.

При выполнении этого равенства (условия) непрерывная и дискретная функции обратимы между собой, т.е. тождественны. Таким образом, произвольный сигнал, спектр которого не содержит частот выше Fm может быть представлен в виде последовательности импульсов, амплитуда которых равна значению исходного сигнала в дискретные моменты времени kt= а интервалы между ними t = 1/(2Fm).

Из приведенной выше формулировки теоремы Котельникова однозначно следует, что для выбора оптимального шага дискретизации необходимо предварительно провести количественные оценки всех значащих гармоник спектрального разложения исходного непрерывного сигнала, для нахождения величины Fm, т.е.m.

Рассмотрим теперь процедуру квантования сигнала по параметру.

В диапазоне непрерывных значений функции f(t) выбирается конечное число дискретных значений функции, распределенных, например, равномерно по всему диапазону. В произвольный момент времени значение функции f(t) заменяется ближайшим дискретным по параметру значением. Тем самым функция приобретает ступенчатый вид (рис.1.2.):

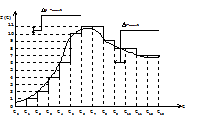
Рис. 1.2. Кривая квантования по параметру

Шагом квантования по параметру называется разность между соседними дискретными значениями функции. Для равномерного квантования шаг квантования постоянный и равен :

k = (fmax _ fmin)/(q _ 1),

где q - число шагов квантования.

Абсолютная погрешность квантования по параметру может изменяться от 0 до k/2. Тогда среднеквадратичная погрешность квантования при равномерном распределении приведенной погрешности от 0 до 0,5k равна:

k = k/2 .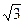

Когда определенному значению квантованного параметра сигнала ставится в соответствие некоторое число (код) из конечного множества выбранной системы счисления, то выполняется процедура кодирования сигнала. Кодированные таким способом сигналы принято называть цифровыми. Однако надо иметь в виду, что кодированием в широком смысле слова называется любое преобразование сообщения в определенный сигнал путем установления между ними однозначного соответствия.

Цифровой сигнал описывается квантованной решетчатой функцией (квантованной последовательность., квантованным временным рядом) Xw(nt), которая принимает ряд дискретных значений уровней квантования h1, h2, h3,..., hk ,, в то время как независимая переменная n = 0, 1, 2,....Каждому из уровней квантования ставится в соответствие некоторое число и тем самым сигнал кодируется. Поэтому передача или обработка отсчета цифрового кодированного сигнала сводится к операциям над безразмерными числами (кодами). Представление сигнала в цифровой форме практически всегда дает существенное преимущество при передаче, хранении и обработке информации.

Следовательно в данном случае информация кодируется конечным набором символов (цифр, букв), которые выбираются из некоторого конечного алфавита. Любую конечную последовательность символов называют словом в данном алфавите. Метод изображения любых чисел с помощь. ограниченного количества цифр называется системой счисления.

Кодирование аналогового сигнала обычно осуществляется при помощи различного типа аналого-цифровых преобразователей (АЦП). Обратная процедура реализуется цифро-аналоговыми преобразователями (ЦАП). Для преобразования сигналов, в частности, используются также различные модуляторы и демодуляторы, широко применяемые, в так называемых, модемах, при помощи которых компьютеры подключаются к различного типа вычислительным сетям. Часто преобразуют и физическую природу сигнала. В частности, преобразование оптического сигнала в электрический и наоборот, выполняют при помощи различных оптоэлектронных устройств.