Изменение внутренней энергии и работа газа в термодинамическом процессе
Под внутренней энергией тела понимается сумма кинетической и потенциальной энергии атомов и молекул.
Внутренняя энергия идеального газа является функцией температуры газа и от давления не зависит: ∆u= φ (Т2) — φ (T1).
Для 1 кг идеального газа изменение внутренней энергии

где сv — теплоемкость газа при v=const. Для элементарного
процесса
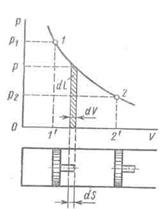
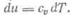
Рис.1.
Графический способ
определения механической работы газа
Механическая работа L газа зависит от характера процесса. Рассмотрим работу произвольного количества газа т (кг) в цилиндре при перемещении поршня с площадью f на расстояние dS, как показано на рис. 1 Ввиду малости dS будем считать давление в цилиндре в процессе этого элементарного перемещения поршня постоянным и равным р. Тогда абсолютная работа, совершаемая газом при расширений, т. е. работа перемещения поршня под действием силы F = pf равна
dL =F dS = pf dS. Изменение объема цилиндра dV = f dS, следовательно, dL = р dV.
Графически элементарная работа dL (см. рис1) соответствует заштрихованной площадке.
Для 1 кг газа элементарная механическая работа газа
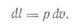
Если величина р переменная, то определение полной работы на участке 1—2 процесса, графическое изображение которого приведено на рис. 1
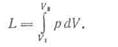
Работа L на участке 1-2 в pv - координатах, соответствует площади 1-2-2'-1', расположенной под кривой, характеризующей процесс.
Для 1 кг газа
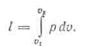
С учетом полученного соотношения для элементарной механической работы газа дифференциальное выражение первого закона термодинамики следующее:
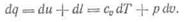
Для конечного процесса с 1 кг газа
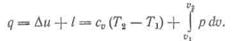
Если учесть, что дифференциальное выражение работы р dv может быть представлено в виде разности pdv=d(pv)-vdp
то равенство примет вид 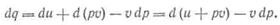
Сумма внутренней энергии и произведения pv представляют функцию состояния тела, называемую энтальпией:
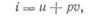
где pv — работа проталкивания, численно равная работе, которую необходимо затратить, чтобы объем v «протолкнуть» в область с давлением р. Например, работа, производимая при подаче 1 кг воды с удельным объемом v0 в паровой котел с давлением р, равна pv0. Величину pv0 иногда называют потенциальной энергией объема.
Таким образом дифференциальное выражение первого закона термодинамики
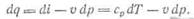
Теплоёмкость газов
Теплоемкостью тела называется количество теплоты, необходимое для повышения его температуры на 1 К. Теплота нагревания, затрачиваемая на
1К единицы количества вещества, называется удельной теплоемкостью. Различают следующие удельные теплоемкости: массовую с (на 1 кг), объемную С (на 1 нормальный м3) и мольную с (на 1 моль).
Соотношение между удельными теплоемкостями следующее:

где μ— молекулярная масса смеси.
Принято удельную теплоемкость называть просто теплоемкостью. Теплоемкость рабочего тела зависит от его природы, температуры тела и характера процесса, в котором происходит подвод или отвод теплоты.
Зависимость теплоемкости газа от его температуры
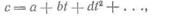
где a, b, d — постоянные коэффициенты, учитывающие физические свойства газа.
Для двухатомных газов достаточную точность дают зависимости с=а+bt.
Теплоемкость зависит от характера процесса. Особое значение имеют теплоемкости газа при постоянном давлении (в изобарном процессе) ср и постоянном объеме (в изохорном процессе) сv. Величина cv меньше ср, так как при нагревании тела в изохорном процессе теплота затрачивается только на повышение температуры. При изобарном нагревании газ расширяется и совершает работу.
Теплота нагревания ср (1 кг газа в изобарном процессе на 1 К) больше теплоты cv на величину работы расширения, которая равна газовой постоянной R. Теплоемкости связаны формулой Майера
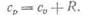
Для мольных теплоемкостей формула Майера
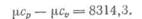
Отношение теплоемкости ср и сv для всех газов больше единицы
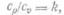
где k — показатель адиабаты.
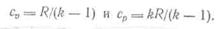
Смеси газов
Рабочее тело тепловых двигателей холодильных машин,
компрессоров и других теплотехнических устройств представляет собой
смесь газов, состав которой может быть задан составом по массе:
в абсолютных количествах
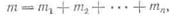
где m1, m2 и т. д. — массы смешиваемых газов;
в относительных долях
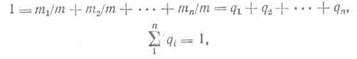
где qi — массовая доля отдельного компонента смеси; или составом по объему:
в абсолютных количествах
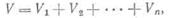
где V1 V2 и Vn — объемы отдельных компонентов при одинаковых физических условиях; в относительных долях;
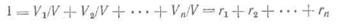
или
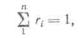
где гi — объемная доля отдельного компонента смеси.
Теплоемкость смеси газов определяется по ее составу. Массовая теплоемкость смеси
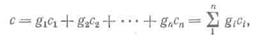
где c1 c2, …. с — массовые теплоемкости отдельных компонентов;
gl g2 ... gn — доли компонентов по массе. Объемная теплоемкость смеси
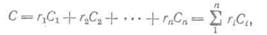
где ri и Ci — соответственно доли компонентов по объему и объемные теплоемкости отдельных компонентов уменьшаются.
Дата добавления: 2020-07-18; просмотров: 570;











