Предел бесконечно числовой последовательности

Бесконечной числовой последовательностьюназывается совокупность чисел, каждому из которых присвоен определенный порядковый номер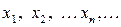

Числовая последовательность задается общим членом 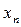, записанным в виде функции номера: 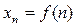. Например, последовательность 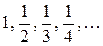задается ее общим членом .

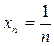Число 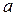называется пределом последовательности 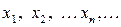, если для всякого сколько угодно малого положительного числа 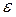(эпсилон) найдется такое положительное число N, что .

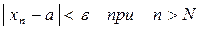В этом случае пишут

.

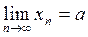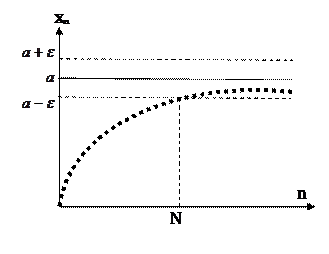( Читается: предел последовательности равен а при n стремящемся к бесконечности).

Рассмотрим геометрический смысл определения предела числовой последовательности. На горизонтальной оси 0n будем откладывать номера элементов числовой последовательности. Тогда вертикальная ось – ось значений элементов числовой последовательности.

Неравенство 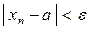эквивалентно системе двух неравенств:

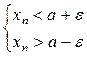Пусть предел числовой последовательности 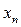равен а. Затем дадим произвольное малое положительное число 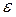. Отложим на вертикальной оси значения , , .

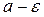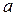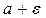Из точек 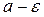, , 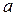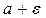на вертикальные оси проведем прямые линии, параллельно горизонтальной оси. Графиком числовой последовательности является множество точек с координатами (1;х₁), (2; х₂), … (n; x_n),… (см. рис)

Начиная с номера N все точки графика числовой последовательности располагаются внутри полосы 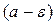, 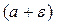. Если задать число 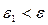, то полоса 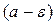, 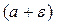будет тоньше. Однако и в этом случае найдется номер числовой последовательности N₁ такой, что при n >N₁ все точки графика будут располагаться внутри полосы.

Числовая последовательность 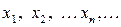называется бесконечно малой, если ее предел при 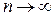равен нулю.

Числовая последовательность называется бесконечно большой, если для каждого сколь угодно большого положительного числа М можно указать такое число N(M) >0, что для всех значений n >N(M) выполняется неравенство 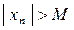. В этом случае пишут: 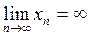. Примером бесконечно малой последовательности является последовательность натуральных чисел 1, 2, 3, …n, …

Предел постоянной величины 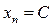равен самой этой величине, так как неравенство 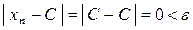выполняется при любых .

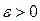Не всякая числовая последовательность имеет предел, например, последовательность с общим членом 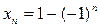. Последовательность имеет вид: 2, 0, 2, 0, 2, 0, … С ростом номера члены числовой последовательности не приближаются к какому то одному числу, для них нельзя указать числа а, для которого выполнялось бы неравенство 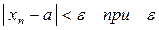> 0

Предел функции 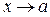при и при .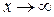

Число b называется пределом функции f(x) при 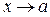(при х стремящемся к а), если для любого сколь угодно малого положительного числа 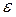(ипсилон) найдется такое число (дельта) 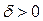, величина которого зависит от 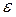, что при всех х, не равных а и удовлетворяющих неравенству 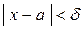, выполняется неравенство .

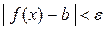Это записывается так

.

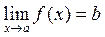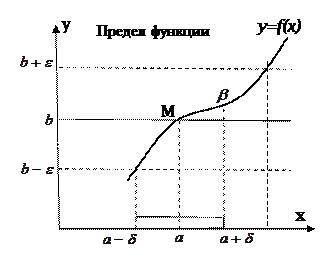Данное определение предела функции имеет геометрическое толкование, которое рассмотрим на рисунке 2. Пусть 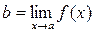. Зададим произвольное малое число 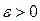. Построим полосу шириной 2 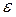со средней линией y=b.

Отобразить с помощью графика функции y=f(x) 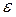-окрестность точки b на оси 0у и получим окрестность точки а на оси 0х. Преобразуем не симметричную окрестность точки а в симметричную с меньшей стороной. Эта окрестность не рисунке подчеркнута и обозначена как , .

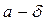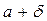Таким образом, для произвольного числа 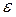мы смогли найти такое число 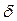, что все точки дуги 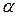, 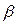графика лежат внутри построенной полосы. При уменьшении числа 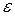полоса сжимается к средней линии, вследствие чего уменьшается 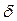- окрестность точки а.

Из определения предела следует:

1) закон, по которому изменяется переменная х при 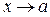, произвольный; х может оставаться по одну сторону от точки а, но может и колебаться относительно этой точки;

2) при любом законе изменения .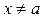

Если 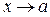и при этом x <a, то пишут 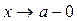. Если 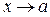и при этом x >a, то пишут .

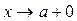В этом случае предел 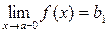называется левосторонним,

предел 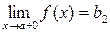называется правосторонним. Для существования предела функции при 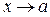необходимо и достаточно, чтобы 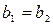. Условно записывают 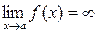, если 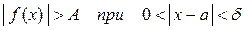, где А – произвольное большое положительное число.

В этом случае функция f(x) называется бесконечно большой при .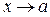

Если 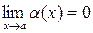, то функция 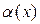называется бесконечно малой при .

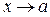Число b называется пределом функции при 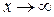, если для любого малого положительного числа 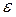можно указать такое положительное число М, величина которого зависит от 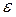, что для всех значений х, удовлетворяющий неравенству 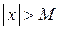, будет выполнятся неравенство .

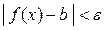Записывается так:

.

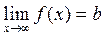Условно записывают 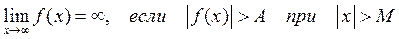, где А – произвольное большое положительное число.

В этом случае функция 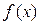называется бесконечно большой при .

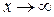Если 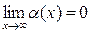, то функция 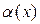называется бесконечно малой при .

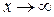Свойства пределов.

Свойства пределов справедливы как для пределов числовых последовательностей, так и для пределов функций. Свойства справедливы как для 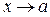, так и для .

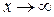1. Предел суммы переменных равен сумме их пределов

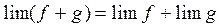
2. Предел произведения переменных равен произведению их пределов

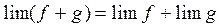
3. Предел дроби двух переменных равен дроби их пределов, если предел делителя отличен от нуля:

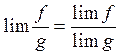, если .

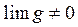4. Постоянный множитель выносится за знак предела

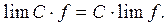
5. Предел постоянной равен самой постоянной

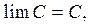где С – соnst.