Кривизна траектории.

Докажем теорему:

Производная от единичного вектора касательной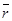

По криволинейной координате S равна по модулю кривизне траектории в данной (.) и направлена по главной нормали в сторону вогнутости.

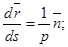
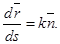К-кривизна траектории.

ρ – радиус кривизны траектории в данной (.)

Ускорение точки

Скорость в общем случаи изменяется по модулю и по направлению.

Мерой изменения скорости (.) с течением времени является ускорение (.) ( )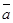

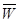
А) Векторный способ задания движения

Движение задано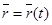

V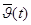

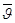
м

м₁ v₁

o

v

∆v

V₁ v_cр

Найдем приращение скорости

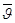∆ за ∆t

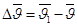
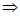
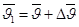
Если 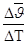- получим среднее ускорение (.) за этот промежуток.

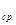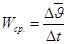
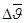Q = . (имеет направление ) т.к. в сторону вогнутости кривой

Lim 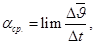получим

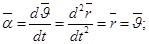
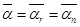
Предельное значение а_ср при t→0 так же направлены внутрь вогнутости кривой.

В) Координатный способ задания движения

x=x(t), y=y(t), z=z(t)

a =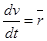

v = v_x*i+v_y*y+v_i*k, r = xi+yi+kz

проектируя на координаты оси

а_x = W_x = v_x = x

а_y = W_y = v_y = y

а_z = W_z = v_z = z

a = a_xi+a_yi+a_zk а=а_xi+a_yj+a_zk

проекция ускорения на декартовых координатах оси выражаются первыми производными от соответствующих проекций скорости ее на те же оси или вторыми производными по времени от соответствующих координат (.)

|a| =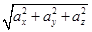

Cos (a,i) = a_x/|a|

Cos (a,j) = a_y/|a|

Cos (a,k) = a_z/|a|

c) Естественный способ задания движения.

S = s(t) и траектория

V = v_rt, где v_t = s =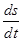

W = 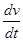= 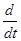(v_rr) = 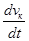r + v_r 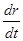= 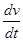r + v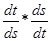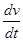_r 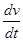= r + r +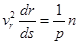

Следовательно

а = 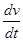r +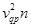

a_r = 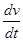r – касательное ускорение

a_n = 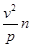- нормальная состояние ускорения.

а = а_r + a_n

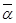- характеризует изменение скорости по величине

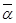- “ – “ - “ изменение скорости по направлению.

Проектируем (**) на естественной оси

М

W 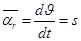(является алгебраической величиной)

W_н W r 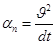(всегда неотрицательная

величина)

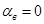
т.е. вектор ускорения всегда лежит в соприкасающей плоскости

Классификация движения (.) по ускорениям ее движения

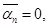
1) 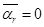(.) движется прямолинейно и равномерно и ее ускорение 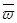=0

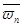2) ≠0, 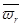≠0 происходит изменение направления скорости без изменения модуля.

(.) движение равномерно криволинейно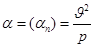

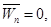
3) 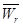≠0 (.) движение по прямой неравномерно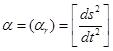

Есл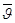и и 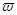совпадают, то движение ускоренное

–“ – “ не совпадают, то замедленное

4) 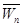≠0, 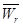≠0 (.) движется неравномерно и криволинейно.

5) Если (W 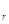)-const . – то (.) совершает равнопеременное движение.

W_t = 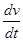= const

Интегрируя при начальных условиях t=0, υ 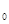=υ, S=S

V = v₀ + w_rt

S = s₀ + v₀t + 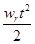w_R – может иметь + или –

Если проекция укоренения на касит. Равна 0

W_r = 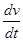=0, то движение называется равномерным

V = v₀ = const

S = S₀ + vt