Решение отсутствует.

Рассмотрим другой пример: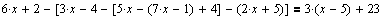

После выполнения описанных выше действий для нахождения решения Mathcad выдает сообщение о том, что решение не найдено.

Проанализировав данное уравнение приходим к выводу, что выданное Mathcad сообщение означает, что решений нет L={}.

MathCAD выдает сообщение "Решение не найдено", даже если уравнение имеет "формальное решение", которое не принадлежит области определения (смотри примеры ниже).

Многозначность.
Если в качестве решения MathCAD выдает имя переменной, это означает, что множество решений уравнения совпадает с областью определения. Однако, такие понятия, как множество решений уравнения и область определения, отсутствуют в MAthCAD и он не выписывает оболасть определения. Вы можете найти область определения, решая с помощью Mathcad систему неравенств или уравнений

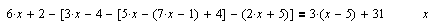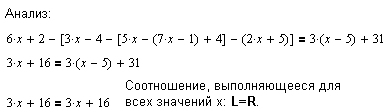
Такой результат, выданный Mathcad после выполнения действий по решению уравнения, означает, что любое значение x из базового множества удовлетворяет этому уравнению, т. е. L=R.

Дробные уравнения

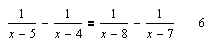
Команда Solve (Вычислить) из подменю Variable (Переменные) меню Symbolics (Символы)выдает множество решений: L = {6}.

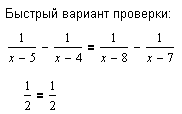
Решение 6 копируем в буфер, а затем выделяем маркером переменную x и активизируем команду Substitute (Замена) подменю Variable (Переменные) меню Symbolics (Символы) для замены переменной значением 6.

Рассмотрим другой пример: 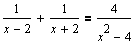Последнее уравнение (рисунок справа) условно эквивалентно уравнению:2x=4. Решение уравнения Mathcad: 2. Формальное решение x = 2 не входит в область допустимых значений. Mathcad выдает правильное сообщение!

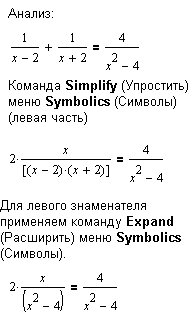
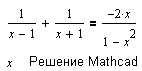
Здесь также правильное решение: множество решений совпадает с областью допустимых значений L = D. Только следует учесть, что D={R\{-1,1}}.

Квадратные уравнения и алгебраические уравнения высших порядков.

Определение: Уравнение P(x)=0 называется алгебраическим уравнением n-го порядка, если P(x) представляет собой полином степени n, при n=2 данное уравнение называется квадратным уравнением.

При решении такого рода уравнения необходимо выполнить те же действия, что и при решении линейных уравнений.