Движение заряженных частиц в плазме
Чтобы нагреть плазму до температуры, соответствующей началу управляемой термоядерной реакции, ее необходимо изолировать от стенок вакуумной камеры и свести до минимума потери горячих частиц из плазмы.
Рассмотрение процессов в системах с магнитным удержанием начнем с анализа поведения заряженных частиц в плазме. Движение этих частиц можно описать, используя три различных подхода:
а) анализ движения отдельных заряженных частиц, невзаимодействующих или слабо взаимодействующих между собой (он проводится обычно в дрейфовом приближении);
б) анализ движения плазмы как сплошной квазинейтральной среды (МГД-приближение);
в) кинетический подход.
Перейдем сначала к наиболее простому описанию поведения невзаимодействующих заряженных частиц в электромагнитных полях, основы которого изучались вами ранее, в курсе «Плазмодинамика». Мы подробно проанализируем движение частиц в стационарных и нестационарных электромагнитных полях сложной конфигурации, характерной для термоядерных систем, и особое внимание уделим на применимости такого подхода к анализу движения частиц в высокотемпературной плазме.
Целью исследований в рамках настоящей лекции является анализ движения заряженных частиц в электромагнитных полях различной геометрии и анализ получающихся траекторий в рамках дрейфового приближения.
Для анализа используем уравнение движения отдельной заряженной частицы с массой M и зарядом Ze в следующем виде:
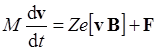 ,
,
где F – равнодействующая всех (кроме силы Лоренца) сил, действующих на частицу (электростатической, гравитационной, силы взаимодействия с другими частицами и т.д.). Мы договорились, что взаимодействие частиц в рассматриваемом приближении отсутствует. Отношение гравитационной силы к другим очень мало. Мы его записывали при анализе величин ядерных сил и их соотношении с другими.
Движение независимой заряженной частицы в электромагнитном поле (т.е. поля влияют на движение отдельных частиц, а обратным влиянием этого движения и соответствующих токов в плазме на магнитную конфигурацию пренебрегается) описывается уравнением, которое в векторной форме в системе СИ имеет следующий вид:
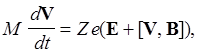
где M, Ze и V- масса, заряд и вектор скорости частицы, t - время, E и B- векторы напряженности электрического и индукции магнитного полей соответственно.
Для трехмерного случая записанное векторное уравнение можно представить в виде системы трех скалярных уравнений для проекций векторных величин. Для правой тройки в декартовых координатах она имеет следующий вид:
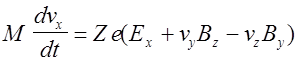
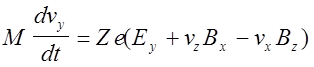
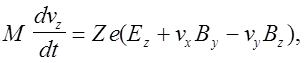
а ее решение для произвольных электромагнитных полей в общем случае может быть проведено численными методами, например методом Рунге - Кутты. Для этого приведенные соотношения записывают в виде системы дифференциальных уравнений первого порядка в форме Коши, т.е. разрешают явно относительно производных. Если задать зависимости характеристик электромагнитного поля от координат, начальное положение и скорость частицы, ее массу и заряд, а также точность решения, применение стандартных процедур интегрирования с автоматическим выбором шага, как правило, не вызывает существенных трудностей.
У нас для проверки этих положений будет специальная лабораторная работа на ЭВМ.
Однако интерпретация полученных таким способом “точных” (т.е. полученных с помощью численных методов с фиксированной погрешностью интегрирования) временных зависимостей координат и проекций скорости для сложных электромагнитных полей может быть затруднена, а поведение частицы становится не совсем понятным. Это связано со сложным и неоднозначным влиянием электромагнитных конфигураций на характер движения частицы. Поэтому в физике плазмы при анализе движения частиц часто используют приближенные модели для его описания, которые позволяют расщепить последнее на ряд составляющих, физическая природа которых достаточно проста, а характер движения частиц довольно легко предсказуем. Однако необходимо отдавать себе отчет в том, что мы получаем таким способом только приближенные результаты, которые могут существенно (как количественно, так и качественно!) отличаться от точного решения уравнения движения. Поэтому обязательным этапом такого приближенного исследования является тщательный анализ применимости использованных упрощений для заданных условий.
Одной из таких моделей является так называемое дрейфовое приближение. При его использовании в движении частицы рассматривают три составляющие, которые связаны не с проекциями вектора скорости на координатные оси, а с их ориентацией относительно вектора магнитной индукции. В рамках этого приближения выделяют следующие элементы движения:
n быстрое вращение частицы вокруг магнитной силовой линии,
n медленный дрейф в направлении, перпендикулярном вектору индукции магнитного поля,
n свободное движение в направлении, коллинеарном вектору B.
Рассмотрим сначала простейшие случаи движения заряженных частиц в конфигурациях, когда присутствует только одно однородное поле (либо электрическое, либо магнитное).
А. Движение частицы в стационарном однородном электрическом поле при отсутствии внешнего магнитного поля B.
Направим вектор Е вдоль оси Ох.
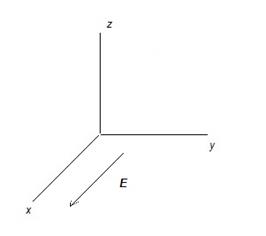
Проекции уравнения движения на оси системы координат принимают вид:
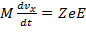 ,
,
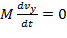 ,
,
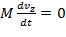 .
.
Электрическое поле изменяет только проекцию скорости на ось Ох. После интегрирования первого уравнения получим для нее выражение
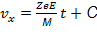 ,
,
а после второго интегрирования – уравнение для временной зависимости координаты х от времени, описывающее равноускоренное движение частица в этом направлении
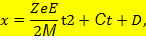
где константы интегрирования C = vx0, D = x0 – начальная проекция скорости частицы и ее начальное местоположение. Естественно, другие координаты частицы и другие проекции скорости не меняются.
Б. Движение частицы в стационарном однородном магнитном поле при отсутствии внешнего электрического поля Е.
Выберем направление вектора магнитной индукции вдоль оси Оz.
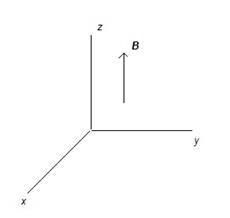
Система трех скалярных уравнений движения в проекции на оси декартовой системы координат (правая тройка) принимает следующий вид:
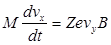 , (1)
, (1)
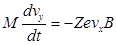 , (2)
, (2)
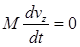 . (3)
. (3)
Продифференцировав первое уравнение по времени, получим:
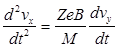 .
.
Подставим сюда из уравнения (2) производную от скорости по y:
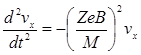 .
.
Аналогично для другой проекции скорости
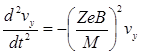 .
.
Эти уравнения суть линейные дифференциальные второго порядка. Характеристическое уравнение имеет вид:
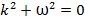 ,
,
а общее решение:
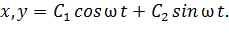
Удовлетворяя граничным условиям, получим
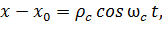
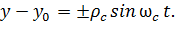
Эти формулы описывают круговую орбиту радиусом 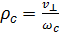 вращения частицы с частотой
вращения частицы с частотой 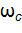 вокруг фиксированного ведущего центра (x0, y0).
вокруг фиксированного ведущего центра (x0, y0).
Характеристиками вращения частицы вокруг магнитной силовой линии являются радиус окружности (называемый циклотронным или ларморовским) 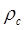 и круговая (или ларморовская) частота
и круговая (или ларморовская) частота 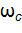 :
:
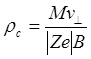 м;
м; 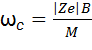 радиан/с,
радиан/с,
где v^ - проекция скорости, перпендикулярная вектору индукции магнитного поля.
Направление вращения частицы всегда таково, что создаваемое при этом магнитное поле направлено противоположно внешнему магнитному полю. Следовательно, частицы плазмы стремятся уменьшить магнитное поле, а плазма является диамагнетиком. Помимо этого движения имеет место еще движение с постоянной скоростью вдоль оси z, т.к. проекция силы на эту ось отсутствует. Говорят, что для такой магнитной конфигурации на движение заряженной частицы вдоль магнитного поля B не действует. Таким образом, заряженная частица в однородном стационарном магнитном поле движется в пространстве по траектории, которая в общем случае является винтовой линией.
Дата добавления: 2020-04-12; просмотров: 559;










