Напряжения на наклонных площадках растянутого стержня

Рассмотрим важный вопрос о том, как зависит величина напряжений от ориентации сечения в растянутом стержне. На рис. 4.1 показано сечение стержня, составляющее угол α с поперечным сечением. Площади поперечного А и наклонного А_α сечений связаны простым соотношением:

А = А_α cos α,

или cos α = А / А_α.

В каждой точке наклонного сечения действует внутреннее полное напряжение р, вектор которого параллелен оси стержня. Действие напряжения р по всей площади А_α количественно характеризуется продольной силой N. Поэтому справедливо равенство:

р А_α = N.

С другой стороны, при растяжении имеем:

N = s А.

где s - величина напряжения в поперечном сечении.

Следовательно, величина внутреннего напряжения меняется в зависимости от угла наклона сечения по закону:

N = р А_α = s А

р = s (А/ А_α) = s cosα

Разложим вектор полных напряжений р на нормальное и касательное напряжения, действующие по наклонной площадке (рис. 4.1). В результате получим следующие зависимости:

s_α =р cos α = s cos ² α, (4.1)

t_α = p sin α = p sin α cos α = 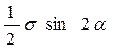(4.2)

Если угол α = 0, s_α = s, t_α = 0.

Если α = π/2, s_α = 0, t_α = 0.

Следовательно, при растяжении силовое взаимодействие между продольными слоями материала отсутствует.

При α = π/4 t_α = t_max = s / 2.

Установим, как связаны напряжения на взаимно перпендикулярных площадках. Для этого положим в формулах (4.1) и (4.2) Ð b = Ð a + 90⁰ и оценим величину напряжений в сечении с углом наклона равным b:

s_b = s cos² b = s cos² (a + 90⁰) = s sin² a.

Величина касательных напряжений на двух взаимно перпендикулярных площадках с учетом соотношения (4.2) может быть оценена аналогичным образом:

.

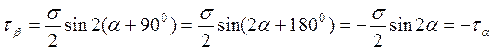Это соотношение носят название закона парности касательных напряжений: на двух взаимно перпендикулярных площадках составляющие касательных напряжений, перпендикулярные к общему ребру, равны и направлены либо к общему ребру, либо от ребра. Закон парности справедлив при любых свойствах материала, а также при любых приложенных нагрузках.

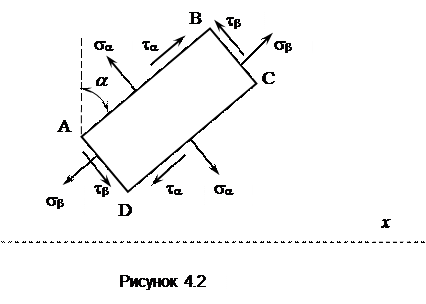Доказывается, что площадку, изображенную на рисунке 4.2, можно развернуть таким образом, что по граням будут действовать только касательные напряжения. Если по граням выделенного элемента действуют только касательные напряжения, то этот элемент испытывает чистый сдвиг.

4.2 Напряжения и деформации при сдвиге

Сдвиг – вид деформации, при котором в поперечном сечении стержня действует только поперечная сила.

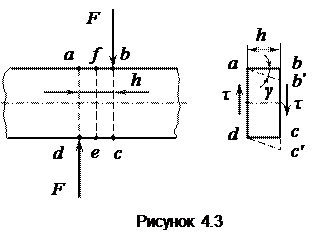Рассмотрим сначала картину силового нагружения стержня, приводящую к сдвигу (рис. 4.3). Пусть две равные, но противоположно направленные силы действуют в поперечных сечениях стержня ad и bc, расстояние между которыми h достаточно мало. Такая картина нагружения возникает, например, при операции резания металлических листов или прутьев. Если увеличивать силу F, то прямые углы элементарного параллелепипеда abcd сначала перекашиваются, а затем происходит срез стержня по некоторому среднему сечению fe. Таким образом, деформация при сдвиге состоит во взаимном смещении близлежащих поперечных сечений относительно друг друга. Величина деформации характеризуется углом сдвига γ, который, равен отношению абсолютного сдвига bb′ к расстоянию h между сечениями действия внешних сил. Под действием внешних перерезывающих сил F возникают равные им внутренние силы Q. Считают, что касательные напряжения t равномерно распределены в сечении стержня, поэтому их величина равна:

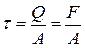(4.3)

Так же как при растяжении (сжатии), напряжения и деформации при сдвиге связаны между собой линейной зависимостью:

t = G g , (4.4)

которую называют законом Гука при сдвиге:в области упругих деформаций касательные напряжения (t) прямо пропорциональны углу сдвига (g). Коэффициент пропорциональности G является еще одной механической характеристикой конструкционных материалов (наряду с модулем продольной упругости Е и коэффициентом Пуассона m). Он называется модулем сдвига. Его значения для различных материалов содержатся в справочной литературе. Размерность модуля сдвига – Па = Н / м ². По физическому смыслу он представляет собой напряжение, которое возникло бы в материале, если бы угол сдвига стал равным 1 радиану (это следует из формулы (4.4)). Для сталей значения модуля G достигают величин @ 0.8 × 10 ¹⁰ Па.

Между модулем упругости и модулем продольной упругости существует взаимосвязь:

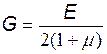(4.5)

4.3 Расчеты на прочность на срез и смятие.

Условия прочности

Срезом называется разрушение в результате сдвига.

Условие прочности на срез:

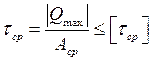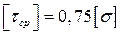, . (4.6)

Условие прочности на смятие:

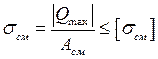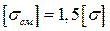, . (4.7)

Допускаемые напряжения 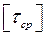и 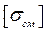принимают по ориентировочным соотношениям в зависимости от допускаемого напряжения на растяжение .

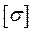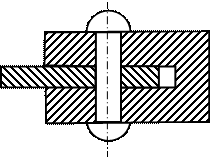
Рассмотрим расчет заклепки, в конструкции соединяющей две детали (рис. 4.4 а) .

		а)
		Рисунок 4.4

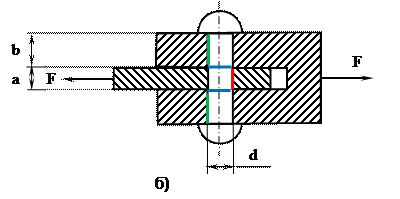
При действии сил F (рис. 4.3 б), растягивающих детали, заклепка будет испытывать срез, две поверхности которого перпендикулярны оси заклёпки. Поверхности среза обозначены двумя горизонтальными синими линиями,

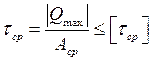, при этом ,

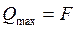суммарная площадь среза, в виде двух кругов равна

.

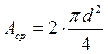Срез сопровождается смятием наименее прочных деталей, входящих в соединение. Заклёпку, как наиболее дешевую деталь, изготавливают из менее прочного материала. Поверхности смятия, обозначены красной (справа от оси заклепки) и зелеными (слева от оси) линиями. Если а < 2b, то смятие будет проходить только по поверхности, обозначенной красной линией.

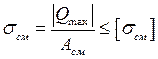, при этом ,

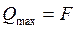где 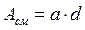– условная поверхность смятия, геометрически равная проекции цилиндра на диаметральную плоскость.

По условию прочности на срез также рассчитывают болтовые, сварные, шпоночные и др. соединения.

4.4 Напряжения и деформации при кручении

Кручение – вид деформации, при котором в поперечном сечении стержня действует только крутящий момент. Стержень, испытывающий деформацию кручения называют – валом. Кручение – это частный случай деформации сдвига, когда в поперечном сечении действуют только касательные напряжения.

При получении расчетных зависимостей используются следующие допущения:

1. Деформации малы и подчиняются закону Гука;

2. Справедлива гипотеза плоских сечений, т.е. слои материала, параллельные плоскости поперечного сечения до деформации остаются плоскими и после деформации, поворачиваясь на некоторый угол относительно оси стержня;

3. Слои материала, параллельные плоскости поперечного сечения, не оказывают давления друг на друга, следовательно, в поперечных сечениях действуют только касательные напряжения, а нормальные напряжения равны нулю.

На рис. 4.5 показан элемент стержня, ограниченный двумя поперечными сечениями с расстоянием между ними dx и цилиндрической поверхностью радиуса r. За счет действия внешнего скручивающего момента Т правое сечение повернется относительно левого сечения на некоторый угол dj. Это перемещение можно рассматривать как сдвиг правого сечения на величину сс΄ (абсолютный сдвиг) и углом сдвига γ. Длину дуги сс΄ можно выразить как через угол поворота dj, так и через угол сдвига γ:

сс΄ = r dφ = γ dx.

Здесь величина тангенса угла сдвига заменена его аргументом в силу малости последнего. Отсюда можно выразить угол сдвига:

.

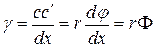Величина 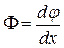называется относительным углом закручивания. Она характеризует угол поворота сечений стержня, приходящийся на единицу его длины.

Правую часть последнего равенства подставим в закон Гука (4.4). Получим соотношение, связывающее напряжения в материале при кручении с величиной перемещений:

t = r G Ф (4.8)

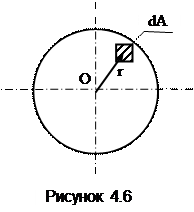
Однако использовать это соотношение при расчетах невозможно, поскольку не известна связь напряжений и перемещений с величиной крутящего момента. Установим ее. Для этого рассмотрим элементарную площадку dA в сечении.

Элементарная сила, обусловленная действием касательных напряжений в пределах площадки dA равна:

dQ = t dA.

Как известно из раздела «Статика», момент этой силы относительно центра сечения О может быть получен как произведение величины силы на плечо:

dT = r dQ = r t dA.

С учетом соотношения (4.8) элементарный момент касательных напряжений, действующих на площадке dA, определяется выражением:

dT = r ^{2 G} Ф dA.

Величина полного момента касательных напряжений относительно центра О может быть получена путем интегрирования этого выражения по всему сечению. С другой стороны, интегральное действие напряжений в сечении характеризуется величиной соответствующего внутреннего силового фактора. В данном случае это крутящий момент Т. Следовательно, справедливо равенство:

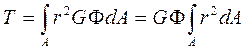(4.9)

Модуль сдвига и относительный угол закручивания вынесены из под знака интеграла, поскольку они не зависят от положения точки в сечении. Интеграл

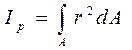(4.10)

носит название полярного момента инерции поперечного сечения стержня и является его геометрической характеристикой. Используя обозначение (4.10), из равенства (4.9) получим следующую формулу для расчета относительного угла закручивания:

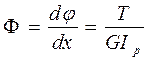(4.11)

Полученное соотношение позволяет количественно оценить перемещения при кручении, если известна зависимость действующего в сечениях крутящего момента от продольной координаты. В самом деле, интегрируя последнее равенство по участку стержня длиной L, получим угол, на который повернется одно крайнее сечение этого участка относительно другого:

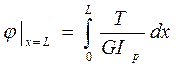(4.12)

Если крутящий момент и сечение стержня не меняются по его длине, то эта формула упрощается:

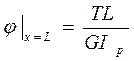(4.13)

Произведение, стоящее в знаменателе, называется жесткостью стержня при кручении.

Полученные для углов поворота формулы позволяют сформулировать условие жесткости при кручении. Так же как и условие жесткости при растяжении, оно состоит в естественном требовании, чтобы максимальные перемещения не превышали допускаемых значений:

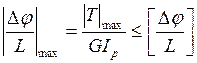(4.14)

Слева в этом неравенстве стоит угол поворота сечений стержня, приходящийся на единицу его длины. Он максимален там, где действует максимальный по абсолютной величине крутящий момент. В правой части неравенства участвует допускаемое значение этой величины, которое для различных элементов оборудования (роторы центрифуг и сепараторов, валы перемешивающих устройств и т. п.) могут меняться в пределах (0.5 – 3.5) · 10 ^-2 рад / м.

Теперь выведем расчетную формулу для определения напряжений при кручении. Для этого в соотношение (4.8) для касательных напряжений подставим правую часть формулы (4.11). В результате получим:

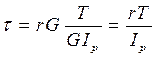. (4.15)

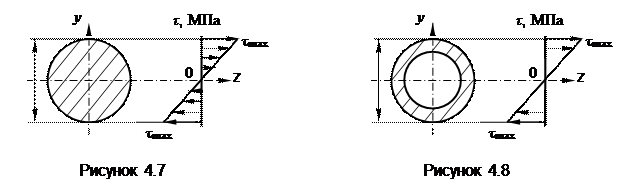
Из полученной формулы видно, что величина касательных напряжений не одинакова в различных точках сечения. В центре сечения при r = 0 напряжения в материале отсутствуют. По мере удаления от центра напряжения увеличиваются пропорционально расстоянию до него, достигая своих максимальных значений на периферии сечения, рис. 4.7. Из эпюры напряжений видно, что центральная часть сечений стержня оказывается недогруженной, следовательно, убирая часть материала, примыкающую к оси стержня, получим рациональную форму поперечного сечения в виде кольца, рис. 4.8.

Из выражения (4.15) следует, что наибольшее значение напряжения в данном поперечном сечении равно

τ_max = r_max T / I_p . (4.16)

Величину W_p = I_p / r_max называют полярным моментом сопротивления поперечного сечения (его размерность м³). Она объединяет все геометрические характеристики сечения, влияющие на величину напряжений.

При эксплуатации элементов оборудования, работающих на кручение, величина максимальных касательных напряжений не должна превышать допускаемых значений [t]. В этом состоит условие прочности при кручении. В символьной форме оно примет вид:

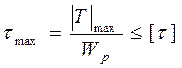(4.16)

Допускаемое значение касательного напряжения [t] для различных конструкционных материалов – величина справочная. Для большинства материалов оно примерно равно половине допускаемого нормального напряжения, т.е. .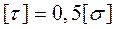

КОНТРОЛЬНЫЕ ВОПРОСЫ ПО ТЕМЕ ЛЕКЦИИ

1. Какие напряжения возникают на наклонных сечениях стержней и как они зависят от угла наклона сечения?

2. Что такое сдвиг и какие напряжения возникают при этом виде деформации?

3. Сформулируйте закон Гука при сдвиге. Запишите формулу для закона Гука при сдвиге.

4. Что такое модуль сдвига и в каких единицах он измеряется?

5. Что называется срезом и смятием?

6. Запишите и поясните условие прочности на срез (сдвиг).

7. Запишите и поясните условие прочности на смятие.

8. Что такое кручение? Когда возникает этот вид деформации? Какие перемещения он вызывает?

9. Какие напряжения возникают при кручении? Как они распределены по сечению стержня?

10. Запишите и поясните формулу для расчета распределения напряжений по круглому поперечному сечению вала при кручении.

11. Запишите и поясните формулу условия прочности при кручении.

12. Сечение, какого вала считается более рациональным – сплошное или кольцевое?

13. Что характеризует относительный угол закручивания? От чего он зависит?

14. Сформулируйте условия прочности и жесткости при кручении.