Итерационные методы

Решение систем линейных уравнений

Прямые методы

Все методы решения линейных алгебраических задач (наряду с задачей решения систем линейных алгебраических уравнений (СЛАУ), это и вычисление определителей, и обращение матриц, и задачи на собственные значения) можно разбить на два класса: прямые и итерационные. Как явствует из заглавия, здесь будут рассмотрены только прямые методы, т. е. такие методы, которые приводят к решению за конечное число арифметических операций. Если операции реализуются точно, то и решение также будет точным (в связи с чем, к классу прямых методов применяют еще название точные методы). Итерационные методы, т. е. методы, в которых точное решение может быть получено лишь в результате бесконечного повторения единообразных (как правило, простых) действий, будут рассмотрены далее.

Другое ограничение будет касаться рассматриваемых систем. Условимся говорить о численном решении таких СЛАУ, у которых число уравнений совпадает с числом вещественных неизвестных, причем будем предполагать наличие единственного решения, если существование и единственность не следует из каких-либо условий.

Такое ограничение здесь довольно естественно, так как решение и недоопределенных, и переопределенных систем, а также систем с комплексными коэффициентами и переменными, в конечном счете, сводится к решению однозначно определенных вещественных систем.

Итак, изучается вопрос о численном решении систем вида

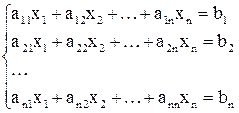(1)

или иначе, векторно-матричных уравнений

Ax = b, (2)

где b = (b₁, b₂, ..., b_n) вектор свободных членов и x = (x₁, x₂, ..., x_n) — вектор неизвестных (он же в другой интерпретации может означать и вектор-решение) с вещественными координатами, а 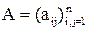— вещественная n´n-матрица коэффициентов данной системы. Эффективность способов решения системы (1) во многом зависит от структуры и свойств матрицы A: размера, обусловленности, симметричности, заполненности (т.е. соотношения между числом ненулевых и нулевых элементов), специфики расположения ненулевых элементов в матрице и др.

Так, размерность системы (т.е. число n) является главным фактором, заставляющим вычислителей отвернуться от весьма привлекательных в теоретическом плане и приемлемых на практике при небольших n (2, 3) формул Крамера

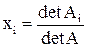(i = 1, 2, ..., n),

позволяющих находить неизвестные компоненты вектора x в виде дробей, знаменателем которых является определитель матрицы системы, а числителем — определители матриц A_i, полученные из A заменой столбца коэффициентов при вычисляемом неизвестном столбцом свободных членов. Если при реализации этих формул определители вычисляются понижением порядка на основе разложения по элементам какой-нибудь строки или столбца матрицы, то на вычисление определителя n-го порядка будет затрачиваться n! операций умножения. Факториальный рост количества арифметических операций (и вообще, очень быстрый рост) с увеличением размерности задачи называют «проклятьем размерности». Что это такое, можно представить, зафиксировав, например, n = 100. Оценив величину 100! » 10¹⁵⁸ и прикинув потенциальные возможности развития вычислительной техники, приходим к выводу о том, что в обозримом будущем системы сотого порядка в принципе не могут быть решены по формулам Крамера. Заметим при этом, что, во-первых, метод Крамера будет неустойчив, т.е. погрешности округлений будут катастрофически нарастать, во-вторых, размерность n = 100 для современных задач не так и велика: довольно часто решаются системы с сотнями и с тысячами неизвестных.

Если осуществлять вычисление обратной матрицы с помощью союзной матрицы, т. е. через алгебраические дополнения, то нахождение решения векторно-матричного уравнений (2) по формуле

x = A^–1b

фактически равнозначно применению формул Крамера и также практически непригодно по упомянутым выше причинам для вычислительных целей.

Метод Гаусса

Наиболее известным и популярным способом решения линейных систем вида (1) является метод Гаусса. Суть его проста — это последовательное исключение неизвестных. В отличие от курса линейной алгебры, нас будут интересовать вычислительные аспекты метода Гаусса, а именно, технология получения вектора-решения x из исходных матрицы A и вектора b, причем, по возможности, минимизирующая влияние неизбежных ошибок округлений. С этой целью, работая с уравнениями системы (1), выведем сначала совокупность формул, позволяющих в итоге получить искомые значения неизвестных, а затем на их основе запишем алгоритм решения поставленной задачи.

Будем поэтапно приводить систему (1) к треугольному виду, исключая последовательно сначала x₁ из второго, третьего, ..., n-го уравнений, затем x₂ из третьего, четвертого, ..., n-того уравнений преобразованной системы, и т.д.

На первом этапе заменим второе, третье, ... , n-е уравнения на уравнения, получающиеся сложением этих уравнений с первым, умноженным соответственно на 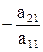, , 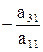..., 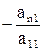. Результатом этого этапа преобразований будет эквивалентная (1) система

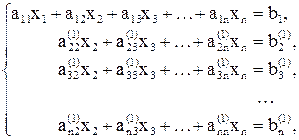(3)

коэффициенты которой (с верхним индексом 1) подсчитываются по формулам

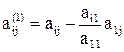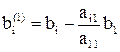, , где i, j = 2, 3, ..., n.

При этом можно считать, что а₁₁ ¹ 0, так как по предположению система (1) однозначно разрешима, значит, все коэффициенты при x₁ не могут одновременно равняться нулю, и на первое место всегда можно поставить уравнение с отличным от нуля первым коэффициентом.

На втором этапе проделываем такие же операции, как и на первом, с подсистемой системы (3), получающейся исключением первого уравнения. Эквивалентный (3) (а значит, и (1)) результат второго этапа будет иметь вид

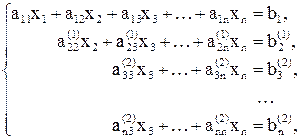
где 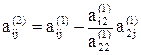, 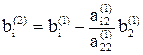; i, j = 3, ..., n.

Продолжая этот процесс, на (n – 1)-м этапе так называемого прямого хода метода Гаусса данную систему (1) приведем к треугольному виду:

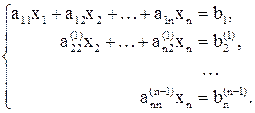(4)

На основе предыдущих рассуждений и формул легко убедиться, что коэффициенты этой системы могут быть получены из коэффициентов данной системы последовательным пересчетом по формулам

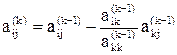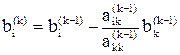, , (5)

где верхний индекс k (номер этапа) должен изменяться от 1 до n – 1, нижние индексы i и j (в любой очередности)— от k + 1 до n; по определению полагаем , .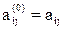

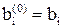Треугольная, точнее, трапециевидная структура системы (4) позволяет последовательно одно за другим вычислять значения неизвестных, начиная с последнего:

,

…,

,

.

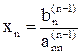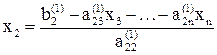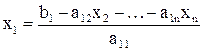Этот процесс последовательного вычисления значений неизвестных называют обратным ходом метода Гаусса. Очевидно, он определяется одной формулой

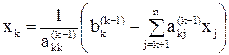, (6)

где k полагают равным n, n – 1, ..., 2, 1 и сумма по определению считается равной нулю, если нижний предел суммирования у знака Σ имеет значение больше верхнего.

Итак, решение СЛАУ вида (1) методом Гаусса сводится к последовательной реализации вычислений по формулам (5) и (6).

Итерационные методы