Решение слау методом простых итераций

Система стандартного вида

Ax = b, (7)

где 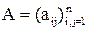— n´n-матрица, а x = (x₁, ..., x_n)^Т и b = (b₁, ..., b_n)^Т — n-мерные векторы-столбцы, тем или иным способом (таких способов существует бесконечное множество; некоторые из них будут рассмотрены ниже) может быть преобразована к эквивалентной ей системе вида

x = Bx + с, (8)

где x — тот же вектор неизвестных, а B и c — некоторые новые матрица и вектор соответственно. Систему (8) можно трактовать, как задачу о неподвижной точке линейного отображения B в пространстве Rⁿ и по аналогии со скалярным случаем определить последовательность приближений x⁽^k) к неподвижной точке x рекуррентным равенством

x⁽^k+1) = Bx⁽^k) + с, k = 0, 1, 2, ... (9)

Итерационный процесс (9), начинающийся с некоторого вектора 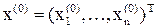, будем называть методом простых итераций (коротко МПИ).

Изучим комплекс вопросов о сходимости этого процесса. А именно:

1) какие нужно предъявить требования к В, с и x⁽⁰⁾, чтобы последовательность (x⁽^k)) при k ® ¥ имела пределом x* — неподвижную точку задачи (8) (и значит, решение эквивалентной (8) исходной системы (7))?

2) с какой скоростью сходится этот процесс, т.е. каков закон убывания абсолютных погрешностей получаемых по формуле (9) приближений?

3) сколько нужно сделать итераций по формуле (9), чтобы при заданном начальном приближении x⁽⁰⁾ найти решение задачи (8) с заданной точностью?

Теорема 1. Необходимые и достаточные условия сходимости МПИ

Необходимым и достаточным условием сходимости метода простых итераций (9) при любом начальном векторе x⁽⁰⁾ к решению x* системы (8) является требование, чтобы все собственные числа матрицы B были по модулю меньше 1.

Теорема 2. Погрешность МПИ

Пусть ||B|| £ q < 1. Тогда при любом начальном векторе x⁽⁰⁾ МПИ (9) сходится к единственному решению x* задачи (8) и при всех k Î N справедливы оценки погрешности:

1) 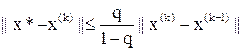(апостериорная);

2) 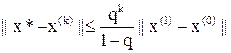(априорная).

Метод Якоби

Вернемся к рассмотрению СЛАУ в виде (7). После выяснения условия, которому должна удовлетворять матрица коэффициентов приведенной системы (8) для сходимости МПИ (9), следует осуществить приведение системы (7) к виду (8) так, чтобы это условие выполнялось. Рассмотрим один из способов такого приведения, достаточно эффективный в определенных случаях.

Представим матрицу A системы (7) в виде

A = L + D + R,

где D — диагональная, a L и R — соответственно левая и правая строго треугольные (т.е. с нулевой диагональю) матрицы. Тогда система (7) может быть записана в виде

Lx + Dx + Rx = b, (10)

и если на диагонали исходной матрицы нет нулей, то эквивалентной (7) задачей вида (8) будет

x = – D^–¹(L + R)x + D^–¹b, (11)

т.е. в равенствах (8) и (9) следует положить

B = – D^–¹(L + R), c = D^–¹b.

Основанный на таком приведении системы (7) к виду (8) метод простых итераций (9) называют методом Якоби. В векторно-матричных обозначениях он определяется формулой

x^(k+1) = – D^–1(L + R)x^(k) + D^–1b, k = 0, 1, 2, ... (12)

Чтобы записать метод Якоби (12) решения системы (7) в развернутом виде, достаточно заметить, что обратной матрицей к матрице 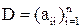служит диагональная матрица D^–1 с элементами диагонали d_ii = 1/a_ii. Поэтому представление (11) системы (7), записанной в виде (10), равнозначно выражению «диагональных неизвестных» через остальные:

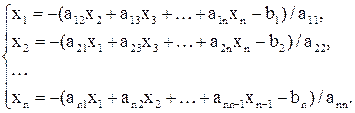(13)

Теперь для записи итерационного процесса (12) осталось в равенствах системы (13) только «навесить» индексы, соответствующие номерам приближений (т.е. k = 0, 1, 2, ...):

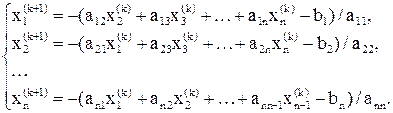(14)

Установим простой достаточный признак сходимости метода Якоби к решению системы (7).

Теорема 3. Достаточный признак сходимости метода Якоби.

В случае диагонального преобладания в матрице A ( 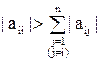"i = 1, …, n) системы (7) метод Якоби (12) сходится.

Теорема 4. Необходимый и достаточный признак сходимости метода Якоби.

Метод Якоби (12) сходится к решению системы (7) в том и только в том случае, когда все корни уравнения

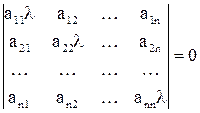
по модулю меньше единицы.

Метод Зейделя

Под методом Зейделя обычно понимается такое видоизменение метода простых итераций (9) решения СЛАУ, приведенных к виду (8), при котором для подсчета i-й компоненты (k + 1)-го приближения к искомому вектору x используются уже найденные на этом, т. е. (k + 1)-м шаге, новые значения первых i – 1 компонент. Это означает, что если система (7) тем или иным способом сведена к системе (8) с матрицей коэффициентов 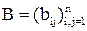и вектором свободных членов 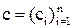, то приближения к ее решению по методу Зейделя определяются системой равенств

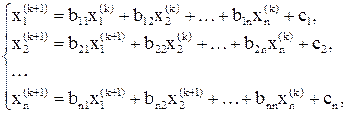(15)

где k = 0, 1, 2, ..., а 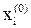— компоненты заданного (выбранного) начального вектора x⁽⁰⁾.

Остановимся подробнее на случае, когда приведение системы (7) к виду (8) основано на представлении (10), т.е. когда метод Зейделя есть модификация метода Якоби. Запись соответствующих расчетных формул здесь сводится к верхней индексации системы (13) по типу (15):

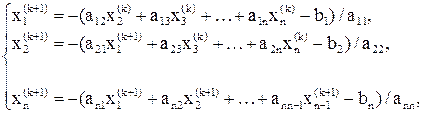(16)

где k = 0, 1, 2, ...; 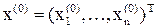задается.

Для анализа сходимости метода Зейделя (16) обратимся к его векторно-матричной форме. Легко видеть, что если неявный вид метода Якоби, вытекающий из представления (10) системы (7), есть

Lx⁽^k) + Dx⁽^k+1) + Rx⁽^k) = b (сравните с (12)),

то равнозначный (16) неявный вид метода Зейделя в векторно-матричных обозначениях суть

Lx^(k+1) + Dx^(k+1) + Rx^(k) = b.

Следовательно, тот же вектор x⁽^k+1) который фигурирует в левой части совокупности равенств (16), может быть получен по формуле

x^(k+1) = – (L + D)^–1Rx^(k) + (L + D)^–1b. (17)

Последнее выражение определяет не что иное, как МПИ (9) для системы вида (8), где

B = – (L + D)^–1R, c = (L + D)^–1b,

т.е. результат применения одного шага метода Зейделя (16), полученного на основе (L + D + R)-разложения матрицы A, можно расценивать как шаг МПИ для эквивалентной (7) задачи о неподвижной точке

x = – (L + D)^–1Rx + (L + D)^–1b (18)

(разумеется, если треугольная матрица L + D обратима). Эта связь между методом Зейделя и методом простых итераций позволяет легко переформулировать некоторые утверждения о сходимости МПИ применительно к методу Зейделя (16).

Теорема 5. Необходимый и достаточный признак сходимости метода Якоби.

Для сходимости метода Зейделя (16) необходимо и достаточно, чтобы все корни уравнения

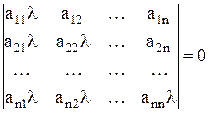(19)

были по модулю меньше единицы.

Прямым следствием Теорема 2 для метода Зейделя (16) является следующая теорема.

Теорема 6. Погрешность метода Зейделя.

Пусть ||(L + D)^–1R|| £ t < 1. Тогда при любом начальном векторе x⁽⁰⁾ метод Зейделя (16) сходится к решению x* системы (7) и справедливы оценки погрешности

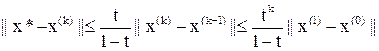(20)