Решение как компромисс и баланс различных интересов. О некоторых ограничениях оптимизационного подхода
Во всех рассмотренных выше задачах выбора и методах принятия решений проблема состояла в том, чтобы в исходном множестве найти наилучшие в заданных условиях, т.е. оптимальные в определенном смысле альтернативы.
Идея оптимальности является центральной идеей кибернетики и прочно вошла в практику проектирования и эксплуатации технических систем. Вместе с тем эта идея требует осторожного к себе отношения, когда мы пытаемся перенести ее в область управления сложными, большими и слабо детерминированными системами, такими, например, как социально-экономические системы.
Для этого заключения имеются достаточно веские основания. Рассмотрим некоторые из них.
1. Оптимальное решение нередко оказывается неустойчивым: т.е. незначительные изменения в условиях задачи, исходных данных или ограничениях могут привести к выбору существенно отличающихся альтернатив.
2. Оптимизационные модели разработаны лишь для узких классов достаточно простых задач, которые не всегда адекватно и системно отражают реальные объекты управления. Чаще всего оптимизационные методы позволяют оптимизировать лишь достаточно простые и хорошо формально описанные подсистемы некоторых больших и сложных систем, т.е. позволяют осуществить лишь локальную оптимизацию. Однако, если каждая подсистема некоторой большой системы будет работать оптимально, то это еще совершенно не означает, что оптимально будет работать и система в целом. То есть оптимизация подсистемы совсем не обязательно приводит к такому ее поведению, которое от нее требуется при оптимизации системы в целом. Более того, иногда локальная оптимизация может привести к негативным последствиям для системы в целом.
3. Часто максимизация критерия оптимизации согласно некоторой математической модели считается целью оптимизации, однако в действительностью целью является оптимизация объекта управления. Критерии оптимизации и математические модели всегда связаны с целью лишь косвенно, т.е. более или менее адекватно, но всегда приближенно.
Итак, идею оптимальности, чрезвычайно плодотворную для систем, поддающихся адекватной математической формализации, нельзя перенести на сложные системы. Конечно, математические модели, которые удается иногда предложить для таких систем, можно оптимизировать. Однако всегда следует учитывать сильную упрощенность этих моделей, а также то, что степень их адекватности фактически неизвестна. Поэтому не известно, какое чисто практическое значение имеет эта оптимизация. Высокая практичность оптимизации в технических системах не должна порождать иллюзий, что она будет настолько же эффективна при оптимизации сложных систем. Содержательное математическое моделирование сложных систем является весьма затруднительным, приблизительным и неточным. Чем сложнее система, тем осторожнее следует относится к идее ее оптимизации.
Поэтому, при разработке методов управления сложными, большими слабо детерминированными системами, основным является не оптимальность выбранного подхода с формальной математической точки зрения, а его адекватность поставленной цели и самому характеру объекта управления.
Существенное отличие СППР от вышеописанных экспертных систем состоит в том, что СППР призвана помочь человеку (ЛПР) в решении стоящей перед ним проблемы, а экспертные системы стараются заменить человека при решении некоторой проблемы.
СППР предоставляют возможность ЛПР оценить (ранжировать) альтернативные варианты решения (далее - альтернативы). Решение о выборе альтернативы принимает человек.
При этом существуют вариант без использования критериев и критериальный вариант.
- Вариант без использования критериев оценки альтернатив.
В этом случае СППР должна решить следующие задачи:
- сформировать множество альтернативных вариантов решения,
- получить результаты сравнения (например, попарного) альтернатив,
- выбрать лучшую альтернативу, имеющую наилучший ранг (место), которая и выдается системой в качестве рекомендации.
Пример1:
Для множества {a,b,c,d,e} считаем, что: c > d > a = e > b.
Тогда результат с номерами рангов
| № ранга | Альтернатива |
| c | |
| d | |
| a, e | |
| b |
В итоге мы получили структурированное множество, не используя понятия "критерий".
Пример 2. "Метод строчных сумм".
Для реализации метода, прежде всего, нужно построить таблицу парных сравнений. Для вышеприведенного примера она выглядит следующим образом.
| a | b | c | d | e | ||
| a | *** | ½ | 1,5 | |||
| b | *** | |||||
| c | *** | |||||
| d | *** | |||||
| e | ½ | *** | 1,5 |
Наименования строк и столбцов соответствуют именам альтернатив. На пересечении строки и столбца ставятся числа по следующим правилам:
- ставится 1, если альтернатива с именем строки лучше альтернативы с именем столбца,
- ставится 0, если альтернатива с именем строки хуже альтернативы с именем столбца,
- ставится 1/2, если альтернатива с именем строки равноценна альтернативе с именем столбца.
Клетки таблицы, у которых имя строки совпадает с именем столбца, не заполняются (в нашем примере в этих клетках проставлены "звездочки"). Затем подсчитываются суммы строк (в примере - числа в крайнем справа столбце). Наконец, строится ранжировка альтернатив следующим способом. Альтернативе, имеющей максимальную строчную сумму присваивается ранг 1. Альтернативе, имеющей следующую по величине сумму, присваивается ранг 2 и так к далее, пока не будут отранжированы все альтернативы. В итоге, получаем ранжировку:
| № ранга | Альтернатива |
| с | |
| d | |
| a,e | |
| b |
Критериальный вариант оценки альтернатив.
При использовании критериальный варианта СППР необходимо решать задачи :
- сформировать множество альтернатив,
- сформировать множество критериев оценки альтернатив,
- получить оценки альтернатив по критериям,
- выбрать лучшую альтернативу, которая и выдается системой в качестве рекомендации.
Критерии иногда удобно группировать в виде дерева (иерархии). Например, в Америке получил большое распространение метод анализа иерархий, предложенный Саати.
В этом случае, исходная модель имеет вид следующей таблицы.
| k1 | >k2 | ... | km | |
| a1 | x11 | x12 | ... | x1m |
| a2 | x21 | x22 | ... | ... |
| ... | ... | ... | ... | ... |
| an | xn1 | xn2 | ... | xnm |
Имена строк представляют имена альтернатив, имена столбцов - имена критериев. На пересечении i-й строки и j-го столбца записывается оценка xij альтернативы ai по критерию kj Такую форму представления модели выбора называют "критериальной таблицей".
Наиболее часто используемый метод упорядочивания таблицы – это линейная свертка. (взвешенная сумма). Сначала некоторым образом выбираются весовые коэффициенты критериев. Обозначим их вектором (w1 , w2 ,... , wm). Затем, для каждой альтернативы (каждой i-ой строки таблицы) рассчитывается следующая величина:
si = å xij wj (сумма берется для всех j от 1 до m).
Результат: чем больше значение si, тем лучше альтернатива ai.
Оценки xij выставляются экспертом или группой экспертов- специалистами в данной предметной области.
При формировании группы экспертов целесообразно провести тестирование, взаимооценку экспертов и проверку согласованности мнений.
Тестированиесостоит в решении экспертами задач, с известными организаторам тестирования, но неизвестными экспертам результатами. Самооценка состоит в том, что каждый эксперт в ограниченное время отвечает на вопросы специально составленной анкеты. Такое испытание проводят на компьютере и затем получают балльную оценку. Эксперты могут оценивать и друг друга, но для этого необходима доверительная обстановка и опыт совместной работы. Согласованность мнения экспертов можно оценивать по величине коэффициента конкордации W, который можно оценить по формуле:
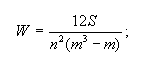
где S - сумма квадратов отклонений всех оценок рангов каждого объекта экспертизы от среднего значения;
n - число экспертов;
m - число объектов экспертизы.
Коэффициент конкордации изменяется в диапазоне 0<W<1, причем 0 - полная несогласованность, 1 - полное единодушие.
Пример
Необходимо определить степень согласованности мнения пяти экспертов, результаты ранжирования которыми семи объектов приведены в таблице:
| Номер объекта экспертизы | Оценка эксперта | Сумма рангов | Отклонение от среднего | Квадрат отклонения | ||||
| -5 | ||||||||
| -13 | ||||||||
Оцениваем среднеарифметическое число рангов:
Qср = (21 + 15 + 9 + 28 + 7 + 25 + 35)/7 = 20.
Затем оцениваем сумму квадратов отклонений от среднего: S = 630.
Определяем величину коэффициента конкордации:
W = 12 * 630 / 25 * (343 - 7) = 0,9.
В этом случае можно говорить о высокой согласованности экспертов.
Пример метода анализа иерархий Саати
Необходимо выбрать автомобиль
Альтернативы:
- Жигули
- Wolkswagen
- Opel
- Fiat
Критерии:
- стиль
- надежность
- экономия топлива
В модели АНР принята иерархия:
Уровень 0 : Цель - выбрать автомобиль.
Уровень 1: Критерии
– стиль
– надежность
– экономичность
Отметим, что уровней может быть сколько угодно. Например, критерий 1-го уровня "надежность" можно раскрыть уровнем 2 как: 1) надежность двигателя, 2) надежность кузова, 3) надежность ходовой части. Надежность ходовой части можно далее раскрыть уровнем 3, например, как а) надежность тормозной системы, б) надежность подвески и т.д.
Теперь нужно получить оценки каждой альтернативы по каждому критерию.
Если существуют объективные оценки, то они просто выписываются и нормируются таким образом, чтобы их сумма была равна единице. Например, если бы нас интересовал критерий "максимальная скорость" и имелись бы соответствующие данные по каждому автомобилю, то нужно было бы составить следующую таблицу.
| Альтернативы | Максимальная скорость (км/час) | Нормированное значение |
| Жигули | 0,209 | |
| Wolkswagen | 0,284 | |
| Opel | 0,269 | |
| Fiat | 0,238 | |
| Сумма | 1,000 |
Для критерия "стиль" не существует объективных оценок. В этом случае процедура Саати рекомендует использовать парные сравнения. Для фиксации результата сравнения пары альтернатив может использоваться, например, шкала следующего типа:
| равноценность | |
| умеренное превосходство | |
| сильное превосходство | |
| очень сильное превосходство | |
| высшее (крайнее) превосходство |
Лицо, принимающее решение (ЛПР), просят попарно сравнить альтернативы. Результат парных сравнений альтернатив для критерия "стиль" записывается в виде таблицы:
| Жигули | Wolkswagen | Opel | Fiat | |
| Жигули | 1/7 | 1/5 | 1/3 | |
| Wolkswagen | ||||
| Opel | 1/3 | |||
| Fiat | 1/5 | 1/3 |
Простые дроби в клетках трактуются следующим образом. Например, на пересечении строки " Wolkswagen " и столбца "Жигули" записано число 7. Это выражает мнение ЛПР о том, что "стильность" Wolkswagen " в 7 раза выше, чем "стильность" Жигулей. В соответствующей клетке пересечения строки Жигули" и " Wolkswagen " записывается обратная величина 1 /7. Таким способом заполняется вся таблица. Далее простые дроби переводятся в десятичные и каждая строка суммируется.
| Жигули | Wolkswagen | Opel | Fiat | Сумма по строке | |
| Жигули | 0,143 | 0,2 | 0,333 | 1,676 | |
| Wolkswagen | |||||
| Opel | 0,333 | 9,33 | |||
| Fiat | 0,2 | 0,333 | 4,533 | ||
| Сумма | 31,539 |
Эта таблица есть не что иное, как таблица результатов парных сравнений.
Теперь, в отличие от таблицы сравнения скоростей, нормируем суммы таким образом, чтобы их сумма в свою очередь была равна 1. Для этого просто разделим сумму каждой строки на 31,539 (сумма последнего столбца, т.е. сумма самих строчных сумм). Получим:
| Жигули | Wolkswagen | Opel | Fiat | Сумма | |
| Жигули | 0,143 | 0,2 | 0,333 | 0,053 | |
| Wolkswagen | 0,507 | ||||
| Opel | 0,333 | 0,295 | |||
| Fiat | 0,2 | 0,333 | 0,145 | ||
| Сумма | 1,0 |
В методе Саати полученные таким образом нормированные суммы принимаются в качестве оценок альтернатив по критерию "стильность".Отметим, что полученные оценки отражают исключительно точку зрения конкретного ЛПР. На самом деле, вместо строчных сумм Саати рекомендует использовать собственный вектор матрицы парных сравнений, считая его более точной оценкой. (Собственными значения li 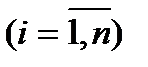 квадратной матрицы A называются действительные или комплексные числа, удовлетворяющие условию:
квадратной матрицы A называются действительные или комплексные числа, удовлетворяющие условию:
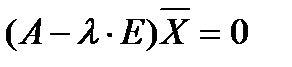 ,
,
E – единичная матрица, 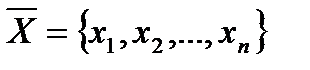 - собственный вектор матрицы A, соответствующий некоторому собственному значению l.
- собственный вектор матрицы A, соответствующий некоторому собственному значению l.
Значения l вычисляются по определителю матрицы А - характеристическому определителю, а затем по найденным l i находится собственный вектор 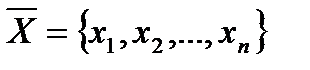 )
)
Строчные суммы, которые допустимы, с точки зрения Саати, менее точны.
Аналогичным образом получаются веса критериев wj . Предположим, конкретное ЛПР сравнило попарно критерии с точки зрения их сравнительной важности. Запишем результаты сравнений в виде таблицы:
| Стиль | Надежность | Экономичность | |
| Стиль | 1/5 | ||
| Надежность | |||
| Экономичность | 1/3 | 1/3 |
Применяя выше описанную процедуру, получим:
| Стиль | Надежность | Экономичность | Сумма | |
| Стиль | 0,2 | 0,23 | ||
| Надежность | 0,65 | |||
| Экономичность | 0,333 | 0,333 | 0,12 | |
| Сумма | 1,0 |
Таким образом, получим веса критериев:
w1 = 0,23 (стиль), w2 = 0,65 (надежность), w3 = 0,12 (экономичность).
Повторяя процедуру парных сравнений для надежности и экономичности по каждому автомобилю можно получить, например, такую таблицу:
| Стиль | Надежность | Экономичность | |
| Жигули | 0,053 | 0,12 | 0,18 |
| Wolkswagen | 0,507 | 0,343 | 0,288 |
| Opel | 0,295 | 0,297 | 0,302 |
| Fiat | 0,145 | 0,243 | 0,23 |
Далее, применяя линейную свертку (взвешенную сумму), получим следующие оценки альтернатив:
Жигули: 0,053 х 0,23 + 0,120 х 0,65 + 0,18 х 0,12 = 0,012 + 0,078 + 0,022 =0,112
Wolkswagen: 0,507 х 0,23 + 0,343 х 0,65 + 0,288 х 0,12 = 0,117 + 0,223 + 0,035= 0,375
Opel: 0,295 х 0,23 + 0,297 х 0,65 + 0,302 х 0,12 = 0,068 + 0,193 + 0,036= 0,297
Fiat: 0,145 х 0,23 + 0,243 х 0,65 + 0,230 х 0,12 = 0,033 + 0,158 + 0,028= 0,219
По выше указным критериям рекомендуется выбрать автомобиль Wolkswagen.
Наибольшие проблемы возникают с обоснованием критериев. Прежде всего, не всегда удается обосновать тот набор критериев, который необходим и достаточен для решения задачи принятия решения. Еще сложнее обстоит дело с весами критериев. Можно даже сказать, что веса критериев – самое тонкое место в проблеме критериального упорядочения альтернатив. Чаще всего веса назначают, исходя из интуитивного представления о сравнительной важности критериев.
Отметим, что в таблице могут оказаться альтернативы, которые имеют оценки по всем критериям хуже, чем другие альтернативы. Сразу ясно, что такие альтернативы неконкурентоспособны. Их можно смело вычеркивать из таблицы. После вычеркивания заведомо наихудших альтернатив, в таблице остаются только такие альтернативы, которые хотя бы по одному критерию, не хуже, чем другие. Множество таких альтернатив получило название "множество недоминируемых альтернатив", или "множество Парето".
Ориентация на компьютерные информационные технологии позволяет основные функции СППР реализовать аппаратно-программными средствами. При этом реализация автоматизированных СППР возможна в как в локальном, так и в сетевом варианте (SQL- технологии, Web- технологии).
Традиционно в качестве областей применения СППР выделяют: микроэкономику, макроэкономику, офисную деятельность, оценку и распространение технологий, юриспруденцию, медицину и другие приложения.
Прогнозирование и планирование деятельности предприятий (от мелких фирм до крупнейших корпораций) является наиболее перспективной сферой практического применения СППР. Для решения проблем в этой сфере в состав СППР включают большой набор методов и моделей, в том числе математическое программирование, статистический анализ, теорию статистических решений и принятия решений при неопределенности, эвристические методы, включающие адаптивность и обучение при решении слабоструктурированных задач, методы теории игр и многие другие подходы.
Дата добавления: 2016-06-22; просмотров: 2211;











